Keras中那些学习率衰减策略_keras学习率策略

神经网路的训练绕不开的调参，调参中学习率至为重要。下面聊聊Keras中提供的学习率策略。

从optimizer的SGD说起

最常见的就是SGD和Adam。这里以SGD为例，看看在模型训练过程中，学习率是如何改变的。
参考官方文档，SGD的定义如下：

tf.keras.optimizers.SGD(
    learning_rate=0.01, momentum=0.0, nesterov=False, name='SGD', **kwargs
)
1
2
3

梯度下降算法中，一般情况下权重${\theta }_t$的更新方法如下式，其中$g_t$表示求得的梯度。
$${\theta }_t={\theta }_{t-1}-learning\_rate\ast g_t$$
当考虑momentum优化方法时，更新方式变为如下：
$$v_t=momentum\ast v_{t-1}-learningrate\ast g_t$$
$${\theta }_t={\theta }_{t-1}+v_t$$

（1）自定义 time-Based Learning Rate Schedule(基于时间的学习率计划)

具体计算如下：

LearningRate = LearningRate * 1/(1 + decay * epoch)
1

在上述的SGD定义中，**kwargs中有decay这个参数，默认值为0时，学习率不会衰减。
当初始learning_rate=0.1，decay=0.001时，

Epoch	Learning Rate
1	0.1
2	0.0999000999
3	0.0997006985
4	0.09940249103
5	0.09900646517
1
2
3
4
5
6

from  tf.keras.optimizers import SGD
#...
# Compile model
epochs = 50
learning_rate = 0.1
decay_rate = learning_rate / epochs
momentum = 0.8
sgd = SGD(lr=learning_rate, momentum=momentum, decay=decay_rate, nesterov=False)
model.compile(loss='binary_crossentropy', optimizer=sgd, metrics=['accuracy'])
# Fit the model
model.fit(X, Y, validation_split=0.33, epochs=epochs, batch_size=28, verbose=2)
1
2
3
4
5
6
7
8
9
10
11

（2） 四种Keras提供的学习率衰减策略

四种衰减策略分别是ExponentialDecay(指数衰减), PiecewiseConstantDecay(分段常数衰减) , PolynomialDecay(多项式衰减)
InverseTimeDecay(逆时间衰减)。
直接使用方法：
假如当拟合Keras模型时，每100000步衰减一次，基数为0.96

lr_schedule = keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate=1e-2,
    decay_steps=10000,
    decay_rate=0.96)
optimizer = keras.optimizers.SGD(learning_rate=lr_schedule)
1
2
3
4
5

a.指数衰减

定义：

tf.keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate, decay_steps, decay_rate, staircase=False, name=None
)
1
2
3

具体的计算实现：

   def decayed_learning_rate(step):
      return initial_learning_rate * decay_rate ^ (step / decay_steps)
1
2

由此我们可以知道，随着训练step的增加，学习率不断地被更新。
这里的一个step指的是一个batch。

b.分段常数衰减

例如：对于前100001步，学习率为1.0，对于接下来的10000步，学习率为0.5，对于任何其他步骤，学习率为0.1

step = tf.Variable(0, trainable=False)
boundaries = [100000, 110000]
values = [1.0, 0.5, 0.1]
learning_rate_fn = keras.optimizers.schedules.PiecewiseConstantDecay(
    boundaries, values)

# Later, whenever we perform an optimization step, we pass in the step.
learning_rate = learning_rate_fn(step)
1
2
3
4
5
6
7
8

c.多项式衰减

给定一个初始学习率和一个结束学习率，优化过程中使用指定多项式形式从初始学习率降到一个结束学习率，比如用2次、3次多项式。
计算过程如下：

def decayed_learning_rate(step):
  step = min(step, decay_steps)
  return ((initial_learning_rate - end_learning_rate) *
          (1 - step / decay_steps) ^ (power)
         ) + end_learning_rate
1
2
3
4
5

比如：拟合一个模型，在10000步中从0.1衰减到0.01，使用开根式( power=0.5):

starter_learning_rate = 0.1
end_learning_rate = 0.01
decay_steps = 10000
learning_rate_fn = tf.keras.optimizers.schedules.PolynomialDecay(
    starter_learning_rate,
    decay_steps,
    end_learning_rate,
    power=0.5)

model.compile(optimizer=tf.keras.optimizers.SGD(
                  learning_rate=learning_rate_fn),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

model.fit(data, labels, epochs=5)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

d.逆时间衰减

def decayed_learning_rate(step):
  return initial_learning_rate / (1 + decay_rate * step / decay_step)
1
2

以0.5衰减率，decay_step=1拟合模型:

initial_learning_rate = 0.1
decay_steps = 1.0
decay_rate = 0.5
learning_rate_fn = keras.optimizers.schedules.InverseTimeDecay(
  initial_learning_rate, decay_steps, decay_rate)

model.compile(optimizer=tf.keras.optimizers.SGD(
                  learning_rate=learning_rate_fn),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])
1
2
3
4
5
6
7
8
9
10

2. 使用callbacks来实现动态、自定义学习率衰减策略

由于optimizer无法访问 validation metrics，因此使用这些调度对象无法实现动态学习率调度(例如，在验证集中loss不再改善时降低学习率)。然而，callbacks可以访问所有指标，包括 validation metrics。因此，您可以通过使用一个callback来修改优化器上的当前学习率来实现动态修改学习率。实际上，这甚至是内置的ReduceLROnPlateau回调。
当我们使用calllback定义的学习率衰减策略时，optimizer中的学习率衰减策略就会被忽视。

（1）自定义 time-Based Learning Rate Schedule

tf.keras.callbacks.LearningRateScheduler(
    schedule, verbose=0
)
1
2
3

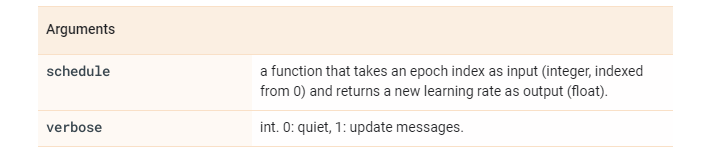
例如：前10个epochs学习率保持不变，后面学习率呈指数衰减

# This function keeps the learning rate at 0.001 for the first ten epochs
# and decreases it exponentially after that.
def scheduler(epoch):
  if epoch < 10:
    return 0.001
  else:
    return 0.001 * tf.math.exp(0.1 * (10 - epoch))

callback = tf.keras.callbacks.LearningRateScheduler(scheduler)
model.fit(data, labels, epochs=100, callbacks=[callback],
          validation_data=(val_data, val_labels))
1
2
3
4
5
6
7
8
9
10
11

（2）Drop-Based Learning Rate Schedule

LearningRateScheduler的callback允许我们定义一个函数来调用epoch number 作为参数并返回随机梯度下降中使用的学习速率。可以定义一个半衰减的学习策略，如下计算公式，DropRate=0.5， floor(Epoch / EpochDrop)计算什么时候更新学习率，当EpochDrop=10时表示每经过10epochs，学习率变为原来的一半。

LearningRate = InitialLearningRate * DropRate^floor(Epoch / EpochDrop)
1

具体实现和使用：

# Drop-Based Learning Rate Decay
import math
from  tf.keras.optimizers import SGD
from  tf.keras.callbacks import LearningRateScheduler

# learning rate schedule
def step_decay(epoch):
	initial_lrate = 0.1
	drop = 0.5
	epochs_drop = 10.0
	lrate = initial_lrate * math.pow(drop, math.floor((1+epoch)/epochs_drop))
	return lrate
# ...
# Compile model
sgd = SGD(lr=0.0, momentum=0.9)
model.compile(loss='binary_crossentropy', optimizer=sgd, metrics=['accuracy'])
# learning schedule callback
lrate = LearningRateScheduler(step_decay)
callbacks_list = [lrate]
# Fit the model
model.fit(X, Y, validation_split=0.33, epochs=50, batch_size=28, callbacks=callbacks_list, verbose=2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

（3）使用ReduceLROnPlateau动态修改学习率

当验证集上的loss几乎不在改变时，修改学习率为原来的2-10倍通常能获得更好的结果。使用ReduceLROnPlateau就能做到。
其定义如下：

tf.keras.callbacks.ReduceLROnPlateau(
    monitor='val_loss', factor=0.1, patience=10, verbose=0, mode='auto',
    min_delta=0.0001, cooldown=0, min_lr=0, **kwargs
)
1
2
3
4

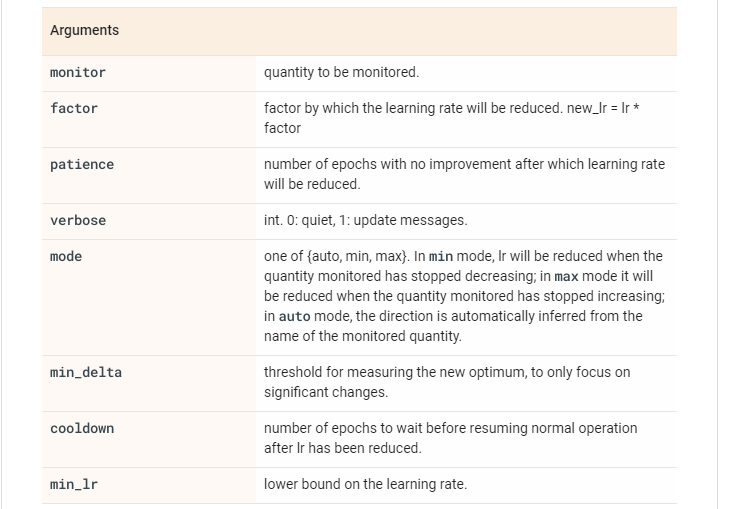
例如当训练集连续5个epochs的改变小于min_delta(默认为0.0001)时，修改学习率为原来的五分之一(new_lr = lr * factor)。

reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.2,
                              patience=5, min_lr=0.001)
model.fit(X_train, Y_train, callbacks=[reduce_lr])
1
2
3

Using Learning Rate Schedules for Deep Learning Models in Python with Keras
Keras官方文档