数据结构 二叉树（一篇基本掌握）

---

绪论

        雄关漫道真如铁，而今迈步从头越。 本章将开始学习二叉树（全文共一万两千字），二叉树相较于前面的数据结构来说难度会有许多的攀升，但只要跟着本篇博客深入的学习也可以基本的掌握基础二叉树。

 

 话不多说安全带系好，发车啦（建议电脑观看）。

---

附：红色，部分为重点部分；蓝颜色为需要记忆的部分（不是死记硬背哈，多敲）；黑色加粗或者其余颜色为次重点；黑色为描述需要

目录

1.树的概念

2.二叉树

2.1二叉树的概念

2.2二叉树的顺序结构

2.2.1堆：

堆的实现（所要实现的功能）：

向上、下调整的应用：

1.向上、向下调整直接建堆的方法：

2.通过大小堆来实现排升、降序

堆的TopK问题：

2.3二叉树的链式结构

2.3.1前序、中序、后序

2.3.1.1当给定前序 / 后序 + 中序就能确定唯一的二叉树（考试常考点）

2.3.2求二叉树中的节点个数：

2.3.3求二叉树的高度

2.3.4求二叉树中第K层的节点

2.3.5在二叉树中查找节点

进阶练习：

2.3.6层序遍历

练习：判断一个二叉树是否为完全二叉树

---

1.树的概念

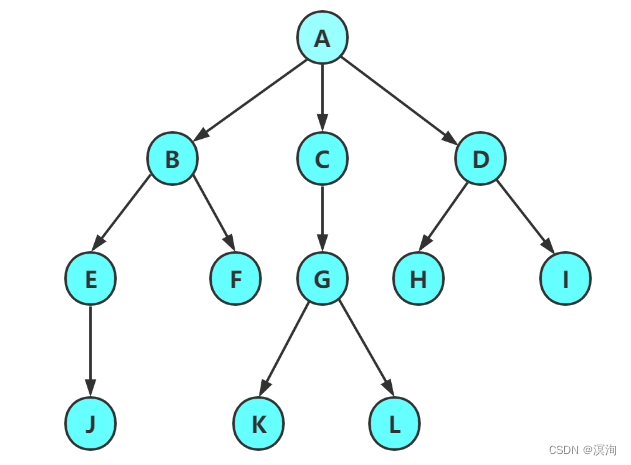
树是一种非线性的数据结构，因为其结构和现实中的树的分叉形式倒过来的样子非常相似故被称为树，其中每个数据被称为一个个 节点，在一棵树中最上面的节点又被称为根节点（根节点没有前驱节点），对于每个节点来说都能称为一个树（或称为子树），每棵树都是由多颗子树构成，并且每个节点都会有且只有一个前驱节点而且由多个或零个后继节点。在树中的各个子树是不能有交集的（互不相交的），一棵有n个节点的树有n-1个父节点（在树中常习惯用亲缘关系来描述）

 

• 父节点（双亲节点）：一个节点的前驱节点（上图A就是BCD的父节点）
• 子节点：一个节点的后继节点（A的子节点有BCD）
• 度：每个节点有的子节点个数（A的度就为3）
• 树的度：在一个树中的所有节点中的最大的度（上面的树其中就是A的度最大故树的度为3）
• 节点的层次：从根开始算，根的层次为1依次往后....（故A的层次为1 、 j 的层次为4）
• 高度（深度）：一般来说也是从1开始的，上图的深度/高度就是4（会有争议有些是从0开始）
• 叶（子）节点（终端节点）：度为0的节点 或者 可以看成没有子节点的节点就是叶节点（如J、K、L、H、I、F）
• 分支节点（非终端节点）：不是叶子节点的节点都算分支节点 或者 度不为0的节点（上图除了叶子节点的其余节点都能看成分支节点）
• 兄弟节点：有相同父节点的节点（如上图的BCD他们都互为兄弟节点）
• 堂兄弟节点：父节点在同一层的节点（如F与G）
• 祖先节点：从根到该节点所经过的所有节点
• 子孙：其节点往后的所有节点都能看成该节点的子孙（上图所有节点都是A）
• 森林：多颗互不相交的树

应用：目录树（由左孩子右兄弟法结构表示）

2.二叉树

2.1二叉树的概念

二叉树是树中的特殊的一种树，其中二叉树的度最大为2，此时的每个节点的子节点称为左孩子、右孩子（左子树、右子树）

 

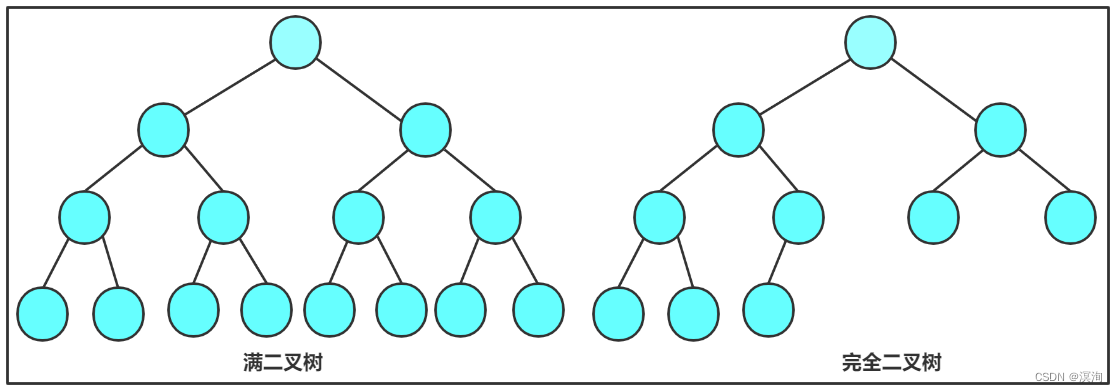
1. 满二叉树：除了叶子结点度为0，其余的节点的度都为2，每一层都是满的        
   1. 一个h层的满二叉树，有（2 ^ h） -  1 个节点
2. 完全二叉树：高度为h的完全二叉树，其前h-1层都是满的，最后一层可以不满，但最后一层必须从左往右是连续的
   1. 一个h层的完全二叉树，有   2 ^（ h - 1）~ （2 ^ h） - 1
3. 在二叉树中 第 h 层的最大节点个数为：2 ^（ h - 1）（若是满二叉树那就直接等于）
4. 一个有h层的二叉树其节点个数最大为（ 2 ^ h ）- 1
5. 对于非空二叉树来说度为0的节点 n0 = 度为2的节点n2 + 1：n0 = n2 + 1
6. 在完全二叉树中度为1的节点只有可能为 1 / 0 ；树的节点个数为偶数时度为1的节点个数是1、奇数时为0

2.2二叉树的顺序结构

二叉树的结构可以由顺序、链表结构实现，对于一般的二叉树来说不适合用顺序结构来存储，因为对于一些没有节点的地方会有许多空间的浪费，完全二叉树很适合用顺序结构，现实中通常把堆（一种二叉树）使用顺序结构的数组存储

2.2.1堆：

1. 为一棵完全二叉树
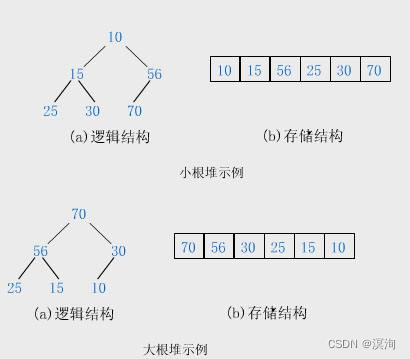
2. 大堆：树中的父节点都大于子节点
3. 小堆：树中的父节点都小于子节点
4. 父节点与子节点的关系
   1. 父节点到左孩子：leftchild = parent * 2 + 1
   2. 父节点到左孩子：leftchild = parent * 2 + 2
   3. 左、右孩子到父节点：parent = （child  - 1） /  2
5. 对于堆结构来说，我们要理解到它的逻辑结构和物理结构
   1. 逻辑结构来说他是一颗完全二叉树
   2. 物理结构来说他的底层是数组来存储的
   3. 我们需要记住他的底层数组来描述这棵完全二叉树

堆的实现（所要实现的功能）：

1. 初始化（主要针对顺序结构所需要的空间）
2. 销毁
3. 插入数据
   1. 堆的向上调整算法
      1. 大概的算法原理：给定孩子的位置和父节点进行比较如果大于/小于则交换（大堆/小堆）循环判断若孩子到了堆顶了停止
      2. 时间复杂度为：O(N*logN)   
4. 删除数据
   1. 堆的向下调整算法
      1. 大概的算法原理：给定父节点和树中的个数，然后让父节点和子节点进行比较如果大于/小于则交换（小堆/大堆）循环判断若孩子节点不存在时停止
      2. 时间复杂度为：O(N) 
5. 取堆顶的数据、查看堆有几个数据、对堆判空

具体细节会在实现里有详细的注释（注释在我们日后工作中是非常重要的，所以可以写成一种习惯）

 #define _CRT_SECURE_NO_WARNINGS 1
 
#include"Heap.h"
 
 
void If_Add_Capacity(HP* php)
{
	if (php->_size == php->_capacity)//判断已有成员个数是否等于容量,若等则进去
	{
		HPDataType* ptr = (HPDataType*)realloc(php->_a, sizeof(HPDataType) * php->_capacity * 2);//进来后就说明空间不够了，需要开空间
		//一般多直接开辟比容量大两倍的空间 即 对a开辟结构体大小为原capacity两倍的空间
		if (ptr == NULL)
		{
			perror("realloc");
 
			return;
		}
		php->_a = ptr;//因为可能是异地扩容所以还要将ptr赋值给数组a
		php->_capacity *= 2;//容量 乘于 2
		ptr = NULL;//无用的指针置为NULL（好习惯）
	}
}
 
//对于堆的初始化和销毁就不过多赘述了相信通过我前面的几篇文章已经能很好的了解其原理了！
void HeapInit(HP* php)
{
	assert(php);
 
	php->_capacity = 4;
	php->_a = (HPDataType*)malloc(sizeof(HPDataType)* (php->_capacity));
	if (php->_a == NULL)
	{
		perror("php::malloc");
		return;
	}
	php->_size = 0;
 
}
void HeapDestroy(HP* php)
{
	assert(php);
	free(php->_a);
	php->_capacity = php->_size = 0;
	php->_a = NULL;
 
}
 
//----------------------------------------------------------------
void swap(HPDataType* t1, HPDataType* t2)
{
	HPDataType tmp = *t1;
	*t1 = *t2;
	*t2 = tmp;
}
//对于向上调整来说，他能形成大堆/小堆
//此处我们先实现一个小堆
// 
//小堆：树中任意一个位置的父节点都要比子节点小
//父子节点的关系： leftchild = parent * 2 + 1 、rightchild = parent * 2 + 2 、parent = （child - 1）/ 2 
void AdjustUp(HPDataType* a, int child) {
	
	while (child > 0)//循环来进行调整，从数组最后一直要调整到堆顶，顶部时child为0 所以条件是要大于0
	{
		int parent = (child - 1) / 2;//找到父节点
		if (a[parent] > a[child])//判断自己是否小于父节点
		{
			swap(&a[parent], &a[child]);//若小于则进行交换
		}
		else {
			break;//反之只要不小于就退出
		}
		child = parent;//修改子节点的下标，让其不断往上走
	}
}
 
//对于堆的插入我们要知道的是其实他是把数据插入到了一个数组中
//但是要注意的是，如果需要实现一个堆的话 ， 那就必须是大堆 / 小堆
//所以我们不仅仅只是把数据插入数组中，而且还需要对数组中的数据进行排序
//通过排序后让他变成大、小堆
//此处就需要用到  向上调整算法
//向上调整算法的前提是在调整的树(除去刚刚插入的数据外)已经满足大堆/小堆
//而此处的数据是一个个插入的（向上调整后就形成了大堆/小堆）所以就能很好的满足这个前提条件
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
 
	If_Add_Capacity(php);//判断容量是不是满了
	
		//首先将数据插入顺序表的尾部
	php->_a[php->_size] = x;
	AdjustUp(php->_a, php->_size);//就行向上排序让新插入的数据也成功的融入到这个堆中
	php->_size++;//一定不要忘记要增加一下size
 
}
 
//--------------------------------------------------------------------
//向下调整成小堆
//向下调整的原理和向上调整差不多
//只不过反了过来
 
void AdjustDown(int* a, int n, int parent)
{
	//找到小的那个孩子
	//建小堆的话需要父节点小于子节点
	//为什么要找小的孩子呢，因为我们要找到子节点中小的那个孩子，才能避免大的孩子如果大于父节点而小的孩子却小于父节点的情况
 
	//此处用了一种特殊的方法
	//先将左孩子看成小的，再判断如果左孩子小于右孩子的话再改变child即可
	int child = parent * 2 + 1;
	while (child < n)//要判断一下孩子节点是否在size范围内
	{
 
		if (child+1 < n && a[child + 1] < a[child])//细节判断一下child+1这个节点是否存在
		{
			child++;
		}
 
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}	
		else{
			break;
		}
	}
}
//堆的删除数据是将堆顶的数据删除
//而这个删除并不是像顺序表一样的进行覆盖，而是
//先将堆顶的数据和最后的数据进行交换
//交换后size--,这样就表示成把数据删除了，因为访问时是在size范围内进行的
//然后对交换到堆顶的数据进行向下调整(让他保持还原成一个堆，满足堆的条件)
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
 
	swap(&php->_a[0], &php->_a[php->_size - 1]);
	php->_size--;
	AdjustDown(php->_a, php->_size ,0);
}
 
HPDataType HeapTop(HP* php){
	assert(php);
	assert(!HeapEmpty(php));
	return php->_a[0];
}
bool HeapEmpty(HP* php){
 
	assert(php);
 
	return php->_size == 0;
}
int HeapSize(HP* php){
	assert(php);
 
	return php->_size;
}

向上、下调整的应用：

1.向上、向下调整直接建堆的方法：

向上调整：他是在一个堆中进行的，我们从数组的第二个数据开始调整这样就不用管这个前提条件了（因为向上看的话单独的节点可以看成一个堆）

 

向下调整：他左右节点是堆中进行的，我们可以从最后一个叶节点的父节点开始调整这样就不用再考虑前提条件（因为向下看的话单独的节点可以看成一个堆）

 

这样给定一个数组让他变成大、小堆的话，就能通过向上或者向下调整循环来构造出一个堆。

具体如下：

建小堆：（若要建大堆的话在向上下调整函数中改变一下大小与关系即可换成建大堆）

void HeapSort(int* a, int n)
{
	//原理和在堆中插入数据差不多
	//向上调整建小堆
	//从第二个数据开始然后不断往后
	for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}
 
	//向下调整建堆
	//从最后的叶子节点的开始然后不断往前
	for (int i = (n - 2) / 2; i >= 0; i--) // 最后一个叶子节点 n - 1 的父节点（（ n - 1 ） - 1 ）/ 2 
	{
		AdjustDown(a,n,i);
	}
}

2.通过大小堆来实现排升、降序

升序建大堆、降序建小堆

因为我们建大堆时父节w点一定大于子节点，所以此时根节点也就是最大的节点，可以把根节点和最后节点交换，这样最大的就发到了 ， 然后size--把这个节点先排除再进行向下调整就能还原堆 ， 最后循环上面过程最终就能实现升序。

小堆的方法一样就不赘述了。通过代码来看

//通过向下调整建小堆
for (int i = (n - 2) / 2; i >= 0; i--) // 最后一个叶子节点 n - 1 的父节点（（ n - 1 ） - 1 ）/ 2 
{
		AdjustDown(a,n,i);
}
 
int end = n - 1;//找到最后一个节点
while (end > 0)
{
	swap(&a[0], &a[end]);//将最后的节点和堆顶元素交换下
 
	AdjustDown(a, end, 0);//再还原一下堆
 
	--end;//改变尾
}

此处的时间复杂度为：O(N + N*logN)==O(N*logN)

堆的TopK问题：

从堆中取出最大/最小的前K个，建大堆找最大的前K个、建小堆找最小的前K个

方法1：在大堆中 pop k次 就能找到最大的前K个、在小堆中 pop k次找最小的前k个

但这方法有点弊端：需要先建堆，而数据量非常大的时候就需要非常多的空间，这样就会导致内存的不够用，（适用于K比较小的情况）

方法2：若查找最大的前K个，我们可以创建一个K大小的小堆来存放这些数据（这样就避免将所有的数据都申请空间），让后让他们逐一比较当比堆顶的大就能进堆，建小堆的原因：因为是要找最大的前K个，小堆的根节点是最小的数据，只有这样才能把要找的大的数据放进去（大堆的根节点是最大的）

实现：

void TopK(int K)
{
	FILE* p = fopen("TopK.txt", "r");
	if (p == NULL)
	{
		perror("p");
		return;
	}
 
	//建K大小的小堆
	HPDataType* heap_arr = (HPDataType*)malloc(sizeof(HPDataType) * K);
	if (heap_arr == NULL)
	{
		perror("heap_arr::malloc");
		return;
	}
	int i = 0;
	for ( i = 0;i < K; i++)
	{
		fscanf(p, "%d", &heap_arr[i]);
	}
	
	for (int i = (K - 2) / 2; i >= 0; i--) // 最后一个叶子节点 n - 1 的父节点（（ n - 1 ） - 1 ）/ 2 
	{
		AdjustDown(heap_arr, K, i);//对数组进行下下调整建堆
	}
	
	//查看剩下的数据
	HPDataType t = 0;
	while(!feof(p))//fscanf将文件中的数据读完后会设置feof的置为非0的值，故对feof取反
	{
		 fscanf(p, "%d", &t);
 
		if (heap_arr[0] < t)//查看文件中的值是否大于堆顶的数据
		{
			heap_arr[0] = t;//大于的话这进堆
			AdjustDown(heap_arr, K, 0);//然后向下调整，将堆中最小的放到堆顶
		}
	}
 
	//打印堆的数据
	for (i = 0; i < K; i++)
	{
		printf("%d\n", heap_arr[i]);
	}
 
	fclose(p);
 
}
 
void testtopk()
{
	//生成数据放进文件中
	FILE* p = fopen("TopK.txt", "w"); 
	srand((unsigned int)time(0));
	//生成一百万个随机数据放进文件中
	for (int i = 1; i <= 1000000; i++)
	{
		int r = rand() % 10000;
		fprintf(p, "%d\n", r);
	}
	fclose(p);
 
	TopK(10);//从小堆中找最大的前k（10）个
}

2.3二叉树的链式结构

链式二叉树的结构：int val、int* right、int* left，当其左右子树都为NULL时就代表到了最后，即对于链式的二叉树来说主要去查看他的左右子树来进行。

2.3.1前序、中序、后序

前序：根、左子树、右子树、中序：左子树、根、右子树、后序：左子树、右子树、根

这里的根表示访问根节点的数据，而左子树、右子树则表示通过结构去访问左右子树的节点。

 

像上图当左右子树为NULL时就开始返回

前中后序都是在递归的基础上进行的

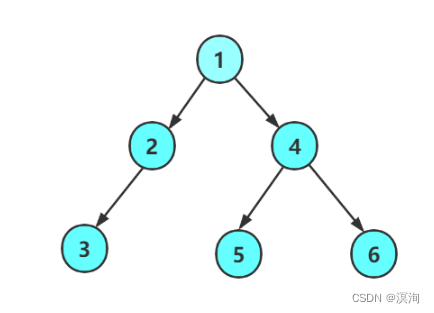
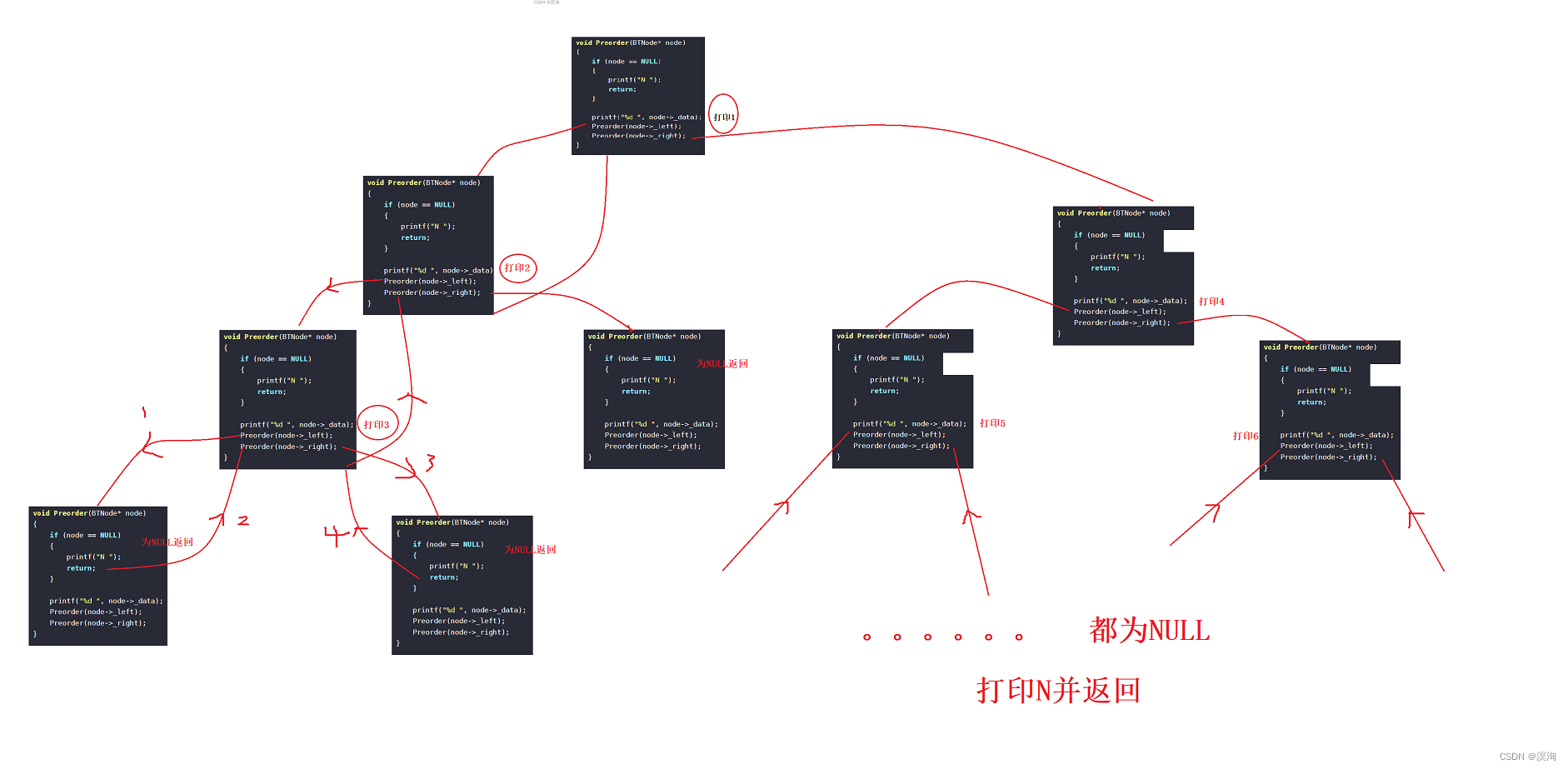
1. 前序遍历为:1 2 3 NULL NULL  NULL  4  5   NULL  NULL  6 N N 
   1. 分析: 前序遍历是先打印所到节点的数据后再往左右子树走遇到NULL则返回
2. 中序遍历为:N 3 N 2 N  1  N  5  N  4  N  6  N
   1. 分析: 中序遍历是先往左子树走遇到NULL则返回  然后再打印所到节点的数据  然后才往右子树走遇到NULL则返回
3. 后序遍历为：N N 3 N 2 N N 5 N N 6 4 1
   1. 分析: 后序遍历是先往左子树走遇到NULL则返回  然后再往右子树走遇到NULL则返回  然后才打印所到节点的数据 

用代码实现 ：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;
 
BTNode* BuyNode(int x)
{
	BTNode* t = (BTNode*)malloc(sizeof(BTNode));
	if (t == NULL)
	{
		perror("malloc");
		return NULL;
	}
	t->_data = x;
	t->_left = NULL;
	t->_right = NULL;
 
	return t;
}
 
void Preorder(BTNode* node)
{
	if (node == NULL)
	{
		printf("N ");
		return;
	}
 
	printf("%d ", node->_data);
	Preorder(node->_left);
	Preorder(node->_right);
}
 
void Inorder(BTNode* node)
{
	if (node == NULL)
	{
		printf("N ");
		return;
	}
 
	Inorder(node->_left);
	printf("%d ", node->_data);
	Inorder(node->_right);
}
 
void Postorder(BTNode* node)
{
	if (node == NULL)
	{
		printf("N ");
		return;
	}
 
	Postorder(node->_left);
	Postorder(node->_right);
	printf("%d ", node->_data);
}
 
 
 
BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	node1->_left = node2;
	node1->_right = node4;
	node2->_left = node3;
	node4->_left = node5;
	node4->_right = node6;
 
	return node1;
}
 
int main()
{
	Preorder(CreatBinaryTree());
	printf("\n");
	Inorder(CreatBinaryTree());	
	printf("\n");
	Postorder(CreatBinaryTree());
		return 0;
}
 

递归展开图（通过这个仔细的了解其原理）：

前序：

 中序、后序就不画了，建议初学者一定要画画

2.3.1.1当给定前序 / 后序 + 中序就能确定唯一的二叉树（考试常考点）

而当给前序+后序的话是不一定能确定唯一二叉树的

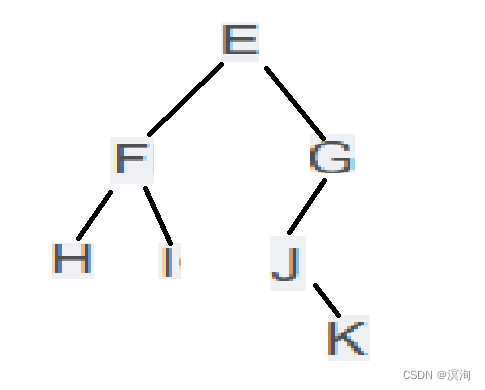
例：前序：EFHIGJK、中序：HFIEJKG

 

因为前序是：根、左、右 ；中序是：左 、 根 、 右

1. 那么前序就能先判断根、而中序能判断左右子树
2. 此时前序先为E
3. 那么中序E的左子树就为HFI 、 E的右子树就是JKG 
4. 再通过前序看根：F他是在中序E的左子树的并且前序先是F故为左子树的根
5. 再通过中序查看F的左右子树为：左：H ； 右：I （因为其内部只有一个节点就不用再排了故就完成了）
6. 此时树的左子树已经完成那就排除掉左边的（EHFI）再继续看右子树（JKG）
7. 同样的方法：通过前序从前往后看根、通过中序看左右子树、然后不断往下直到没有节点
8. 右子树：前序最开始时G故意G为子树的根节点、再看中序只有左节点那么都在左边 再看J为前序的开始那么以J为根、再看中序K在右边那么K为右子树
9. 最终得：

 

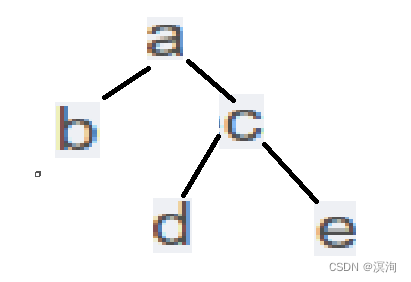
例：后序：bdeca 、中序：badce

此时后序和前序略有不同需要我们从后往前来看

因为后序：左 、右 、根 ； 中序是：左 、 根 、 右

1. 后序中从后往前看树的根为a
2. 然后看中序只有b在左子树，那么在左子树就b一个节点、然后看右子树有（dce）
3. 确定左右子树的节点后再看后序从后往前的倒数第二个为c，那么就表示c为右子树的根（此处要注意此时不同于前序要先看右树的根也就是c）
4. 在看中序就能看出d为右子树的左节点、e为右节点
5. 最终得：

 

 

2.3.2求二叉树中的节点个数：

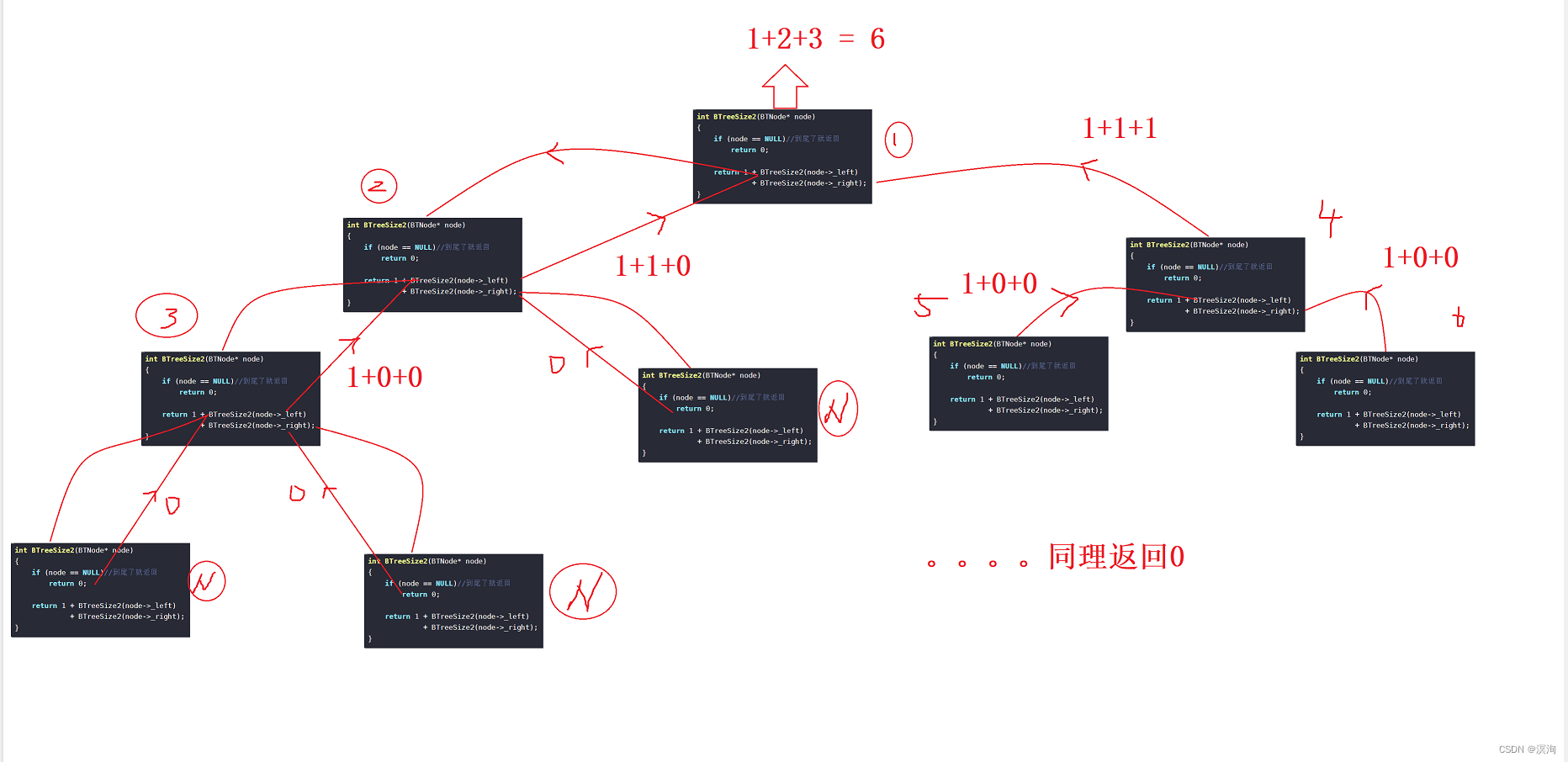
方法1的原理和前中后序一样

int size = 0;//用全局变量来记录节点个数
void BTreeSize1(BTNode* node)
{
 
	if (node == NULL)//当遇到NULL则返回且不记录
		return;
	
	++size;
	BTreeSize1(node->_left);
	BTreeSize1(node->_right);
}
 

方法2原理：返回 自身+左树的所有的节点+右树所有的节点，这样不断递归下去当到NULL时就返回0

int BTreeSize2(BTNode* node)
{
	if (node == NULL)//到尾了就返回
		return 0;
 
	return 1 + BTreeSize2(node->_left) 
		     + BTreeSize2(node->_right);
}

 初学建议一定要画画递归图这样就能更清楚的了解！下面就不画了看不懂可以画画图或者评论区可以提问我都会看！

2.3.3求二叉树的高度

思路：递归思路 ，每个节点记录自己左右子树返回来的值  判断左右孩子那边返回来的值大 ， 最终返回大的一边。

实现：

int BTreeHight(BTNode* node)
{
	if (node == NULL)
		return 0;
 
//记录左右子树返回的值
	int left = BTreeHight(node->_left);
	int right = BTreeHight(node->_right);
 
//返回大的一边，+1是为了算自身
	return left > right ? left + 1 : right + 1;
}

2.3.4求二叉树中第K层的节点

思路：用一个变量记录如果到了第K层就返回1，否则的返回0

实现：

int BTreeLevelKSize(BTNode* node,int k)
{
	assert(k > 0);//防止K不符合实际
 
	if (node == NULL) {//同样的当遇NULL就要返回
		return 0;
	}
 
//到达第K层时，k为1
	if (k == 1) {
		return 1;
	}
 
//左右子树都要加上
	return BTreeLevelKSize(node->_left, k - 1) + BTreeLevelKSize(node->_right, k - 1);
}

2.3.5在二叉树中查找节点

思路：于上面查看二叉树的高度类似，先不断递归再在递归过程中判断其节点的值是否和所要查找的相等，若相等则返回该节点的地址，反之只有当遇空了才返回NULL ， 最后通过记录左右子树的返回情况若为NULL则不用若不为NULL则表示返回来了一个节点指针

实现：

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
 
//查看节点是否为NULL若为则返回
	if (root == NULL)
	{
		return NULL;
	}
 
//判断节点数据是否等于要查找的数据
	if (root->_data == x)
	{
		return root;
	}
 
//记录左右子树的返回
	BTNode* left = BinaryTreeFind(root->_left, x);
	BTNode* right = BinaryTreeFind(root->_right, x);
 
 
//若不为NULL则表示找到了节点返回节点指针即可
	if (left)
		return left;
//用了三目、原理一样
	return right != NULL ? right : NULL;
}

进阶练习：

对称二叉树：

思路：分析题目，为证明树的对称那么就能发现：要判断左子树的左节点和右子树的右节点是否相等、左子树的右节点和右子树的左节点是否相等。

 

那么首先要解决的难题是要抛弃固有思路只从一个节点来看，此时就可以在写一个函数，让其可以同时从左右子树往下查询是否相等

 

并且就能有递归思路：return   _isSymmetric(Leftroot->left ,  Rightroot->right ) && _isSymmetric(  Leftroot->right  ,  Rightroot->left);   左树左子--右树右子、左树右子--右树左子

 

然后就是限制递归的思路：

同时遇NULL表示相等（前面都相等到空树了）那么就表示是相等的返回真
若当只有一方为NULL时是不等的故返回false
再然后 就是判断其值是否相等了

 

最终代码：
 

//关键的如何可以同时在一棵树中往左右走
bool _isSymmetric(struct TreeNode* Leftroot  ,struct TreeNode* Rightroot){
    
    //两个都为NULL
    if(Leftroot == NULL &&  Rightroot == NULL){
        return true;
    }
    //其中一个为NULL
    if(Leftroot == NULL ||  Rightroot == NULL){
        return false;
    }
 
    if(Leftroot->val != Rightroot->val){
        return false;
    }
 
    return _isSymmetric(Leftroot->left,Rightroot->right )
        && _isSymmetric(Leftroot->right,Rightroot->left);
}
 
bool isSymmetric(struct TreeNode* root){
    return _isSymmetric(root->left , root->right);
}

2.3.6层序遍历

层序遍历的方法：通过队列的形式将节点存进队列中，每当有节点出队列时就将其自身的左右节点带进来，这样就能实现对二叉树的层序遍历。

代码实现：

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
//若为NULL就不进去了
	if(root)
		QueuePush(&q, root);
//判断条件队列不为NULL
	while (!QueueEmpty(&q))
	{
//记录在队列最前面的节点
		BTNode* front = QueueFront(&q);
//出队列
        QueuePop(&q);
//打印该节点的值
		printf("%d ", front->_data);
 
//front的左右节点不是NULL则将节点带入
		if (front->_left)
			QueuePush(&q, front->_left);
		if(front->_right)
			QueuePush(&q, front->_right);
	}
}

练习：判断一个二叉树是否为完全二叉树

用层序的思路来查看该二叉树

对于完全二叉树的特性：节点是除了最后一层其余每层都是满的并且从左往右是连续的

则就表示在层序的队列中所有节点都是连续存放的其中不会有NULL插开的情况

bool BTreeCompare(BTNode* root)
{
	Queue q;
	QueueInit(&q);
 
	if (root)
		QueuePush(&q, root);
 
//把节点逐一放进队列中
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		
		//只要第一次NULL就退出
		if (front == NULL)
			break;
 
		QueuePush(&q, front->_left);
		QueuePush(&q, front->_right);
	}
 
//查看队列后面是否全部为NULL若不是就表示不是完全二叉树
//因为完全二叉树的节点是连续的
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
			return false;
	}
	return true;
}

---

如果有任何问题欢迎讨论哈！

如果觉得这篇文章对你有所帮助的话点点赞吧！

持续更新大量数据结构细致内容，早关注不迷路。