【智能优化算法】河马优化算法(Hippopotamus optimization algorithm，HO)

河马优化算法（Hippopotamus optimization algorithm，HO）是发表在中科院二区期刊“Scientific Reports”的文章“Hippopotamus Optimization Algorithm: a Novel Nature-Inspired Optimization Algorithm”上的算法。

01.引言

河马优化算法（Hippopotamus optimization algorithm，HO）是通过从河马观察到的固有行为中汲取灵感而构思的，展示了一种创新的元启发式方法。HO在概念上是使用一个三相模型来定义的，该模型结合了它们在河流或池塘中的位置更新，对捕食者的防御策略和逃避方法，这些都是数学公式。在161个基准函数中，它在寻找最优值方面获得了115个最高排名，包括单峰和高维多峰函数，固定维多峰函数，以及CEC 2019测试套件和CEC 2014测试套件的10、30、50和100维度以及Zigzag模式基准函数，这表明HO在开发和探索方面都表现出了显著的熟练程度。此外，它有效地平衡了探索和利用，支持搜索过程。根据解决四个不同的工程设计挑战的结果，HO有效地实现了最有效的解决方案，同时坚持遵守指定的约束条件。HO算法的性能评估涵盖了各个方面，包括与WOA、GWO、SSA、PSO、SCA、FA、GOA、TLBO、MFO和IWO的比较，后者被认为是研究最广泛的元启发式算法，AOA是最近开发的算法，CMA - ES是高性能优化器，因其在IEEE CEC竞赛中取得成功而得到认可。

02.代码流程

HO从河马生活中观察到的三种突出的行为模式中获得灵感：河马群由几只雌性河马、河马幼崽、多只成年雄性河马和一只占统治地位的雄性河马(兽群的领袖)组成。由于它们天生的好奇心，幼河马和幼河马经常表现出离开群体的倾向。因此，它们可能会被孤立，成为捕食者的目标。河马的第二种行为模式本质上是防御性的，当它们受到捕食者的攻击或其他生物侵入它们的领地时，就会被触发。河马表现出一种防御反应，它们将自己旋转向捕食者，并利用它们强大的下颚和发声来阻止和击退攻击者(图1)。狮子和斑点鬣狗等捕食者意识到这一现象，并积极寻求避免直接接触河马强大的下颚，作为一种预防措施，防止潜在的伤害。最后一种行为模式包含了河马的本能反应，即逃离捕食者并积极寻求与潜在危险区域保持距离。在这种情况下，河马努力向最近的水域航行，比如河流或池塘，就像狮子和斑点鬣狗经常表现出对进入水生环境的厌恶一样。

03.部分代码

%% Designed and Developed by Mohammad Hussien Amiri and Nastaran Mehrabi Hashjin
function[Best_score,Best_pos,HO_curve]=HO(SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness)
lowerbound=ones(1,dimension).*(lowerbound);                              % Lower limit for variables
upperbound=ones(1,dimension).*(upperbound);                              % Upper limit for variables
%% Initialization
for i=1:dimension
    X(:,i) = lowerbound(i)+rand(SearchAgents,1).*(upperbound(i) - lowerbound(i));                          % Initial population
end
for i =1:SearchAgents
    L=X(i,:);
    fit(i)=fitness(L);
end
%% Main Loop
for t=1:Max_iterations
    %% Update the Best Condidate Solution
    [best , location]=min(fit);
    if t==1
        Xbest=X(location,:);                                  % Optimal location
        fbest=best;                                           % The optimization objective function
    elseif best<fbest
        fbest=best;
        Xbest=X(location,:);
    end
    for i=1:SearchAgents/2
        %% Phase1: The hippopotamuses position update in the river or pond (Exploration)
        Dominant_hippopotamus=Xbest;
        I1=randi([1,2],1,1);
        I2=randi([1,2],1,1);
        Ip1=randi([0,1],1,2);
        RandGroupNumber=randperm(SearchAgents,1);
        RandGroup=randperm(SearchAgents,RandGroupNumber);
        % Mean of Random Group
        MeanGroup=mean(X(RandGroup,:)).*(length(RandGroup)~=1)+X(RandGroup(1,1),:)*(length(RandGroup)==1);
        Alfa{1,:}=(I2*rand(1,dimension)+(~Ip1(1)));
        Alfa{2,:}= 2*rand(1,dimension)-1;
        Alfa{3,:}= rand(1,dimension);
        Alfa{4,:}= (I1*rand(1,dimension)+(~Ip1(2)));
        Alfa{5,:}=rand;
        A=Alfa{randi([1,5],1,1),:};
        B=Alfa{randi([1,5],1,1),:};
        X_P1(i,:)=X(i,:)+rand(1,1).*(Dominant_hippopotamus-I1.*X(i,:));
        T=exp(-t/Max_iterations);
        if T>0.6
            X_P2(i,:)=X(i,:)+A.*(Dominant_hippopotamus-I2.*MeanGroup);
        else
            if rand()>0.5
                X_P2(i,:)=X(i,:)+B.*(MeanGroup-Dominant_hippopotamus);
            else
                X_P2(i,:)=((upperbound-lowerbound)*rand+lowerbound);
            end
        end
        X_P2(i,:) = min(max(X_P2(i,:),lowerbound),upperbound);
        L=X_P1(i,:);
        F_P1(i)=fitness(L);
        if(F_P1(i)<fit(i))
            X(i,:) = X_P1(i,:);
            fit(i) = F_P1(i);
        end
        L2=X_P2(i,:);
        F_P2(i)=fitness(L2);
        if(F_P2(i)<fit(i))
            X(i,:) = X_P2(i,:);
            fit(i) = F_P2(i);
        end
    end
    %% Phase 2: Hippopotamus defense against predators (Exploration)
    for i=1+SearchAgents/2 :SearchAgents
        predator=lowerbound+rand(1,dimension).*(upperbound-lowerbound); 
        L=predator;
        F_HL=fitness(L);
        distance2Leader=abs(predator-X(i,:));
        b=unifrnd(2,4,[1 1]);
        c=unifrnd(1,1.5,[1 1]);
        d=unifrnd(2,3,[1 1]);
        l=unifrnd(-2*pi,2*pi,[1 1]);
        RL=0.05*levy(SearchAgents,dimension,1.5);
        if fit(i)> F_HL
            X_P3(i,:)=RL(i,:).*predator+(b./(c-d*cos(l))).*(1./distance2Leader);
        else
            X_P3(i,:)=RL(i,:).*predator+(b./(c-d*cos(l))).*(1./(2.*distance2Leader+rand(1,dimension)));
        end
        X_P3(i,:) = min(max(X_P3(i,:),lowerbound),upperbound);
        L=X_P3(i,:);
        F_P3(i)=fitness(L);
        if(F_P3(i)<fit(i))
            X(i,:) = X_P3(i,:);
            fit(i) = F_P3(i);
        end
    end
    %% Phase 3: Hippopotamus Escaping from the Predator (Exploitation)
    for i=1:SearchAgents
        LO_LOCAL=(lowerbound./t);
        HI_LOCAL=(upperbound./t);
        Alfa{1,:}= 2*rand(1,dimension)-1;
        Alfa{2,:}= rand(1,1);
        Alfa{3,:}=randn;
        D=Alfa{randi([1,3],1,1),:};
        X_P4(i,:)=X(i,:)+(rand(1,1)).*(LO_LOCAL+D.* (HI_LOCAL-LO_LOCAL));
        X_P4(i,:) = min(max(X_P4(i,:),lowerbound),upperbound);
        L=X_P4(i,:);
        F_P4(i)=fitness(L);
        if(F_P4(i)<fit(i))
            X(i,:) = X_P4(i,:);
            fit(i) = F_P4(i);
        end
    end
    best_so_far(t)=fbest;
    disp(['Iteration ' num2str(t) ': Best Cost = ' num2str(best_so_far(t))]);
    Best_score=fbest;
    Best_pos=Xbest;
    HO_curve=best_so_far;
end
end

04.代码效果图

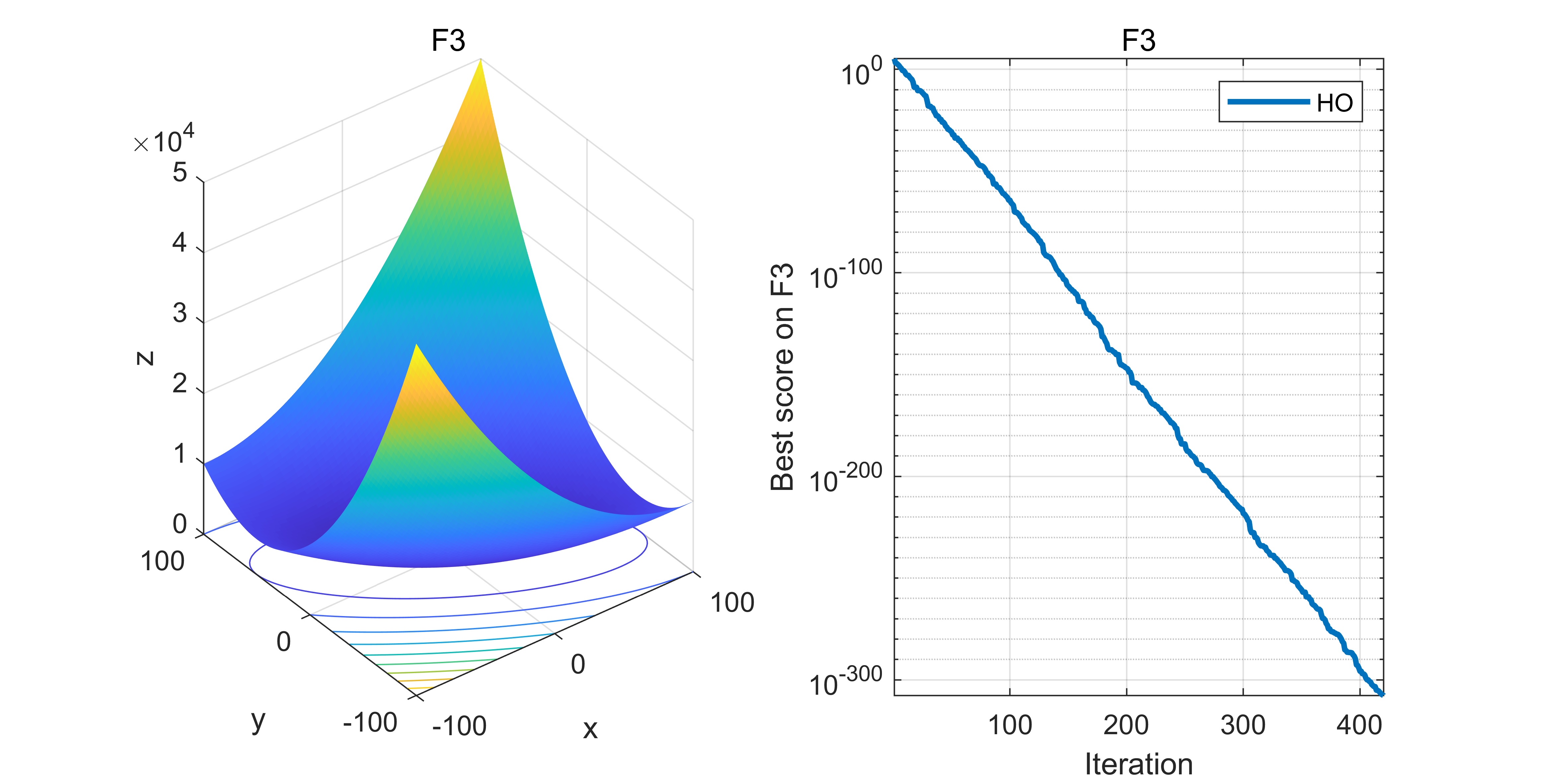
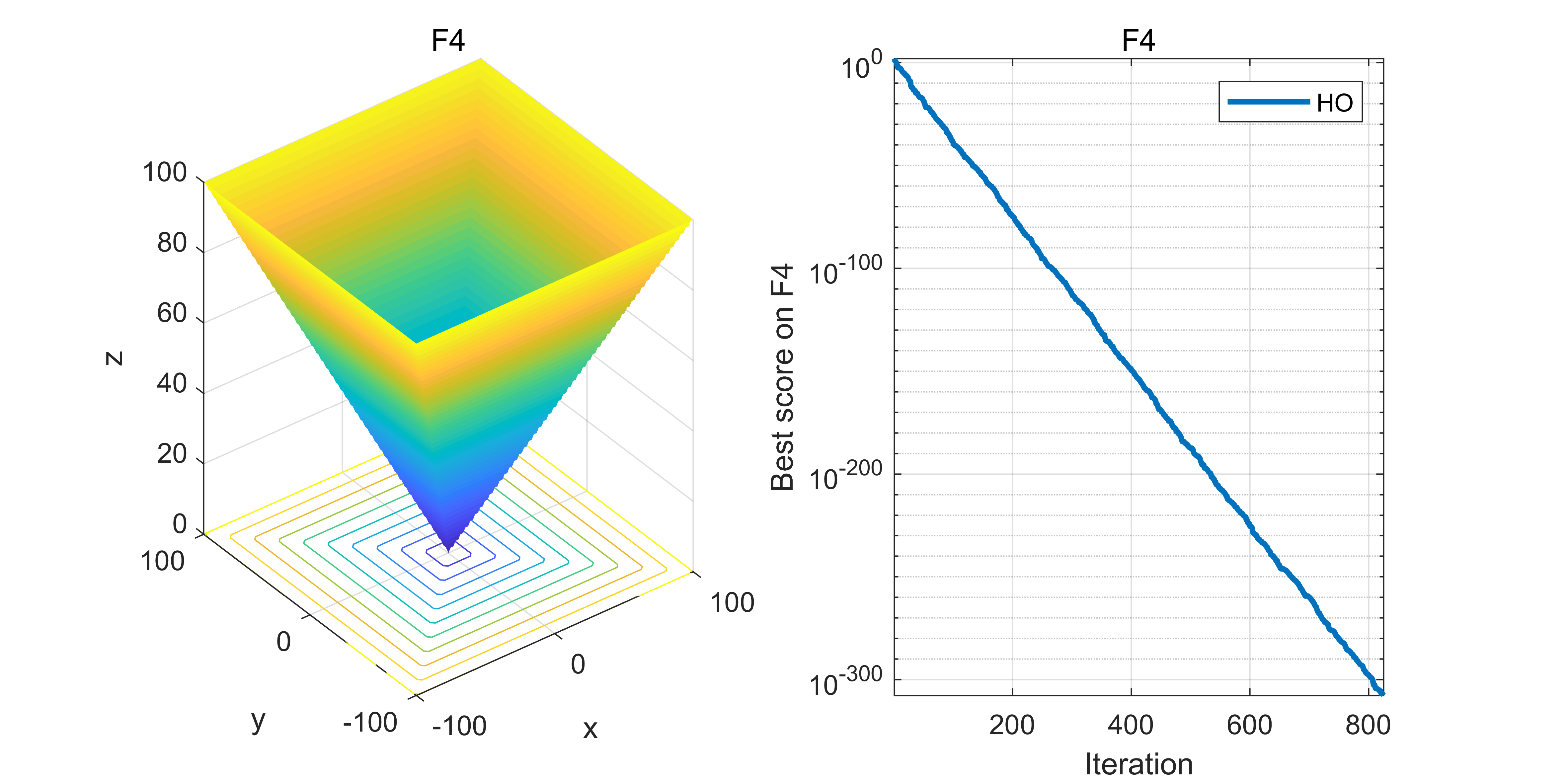
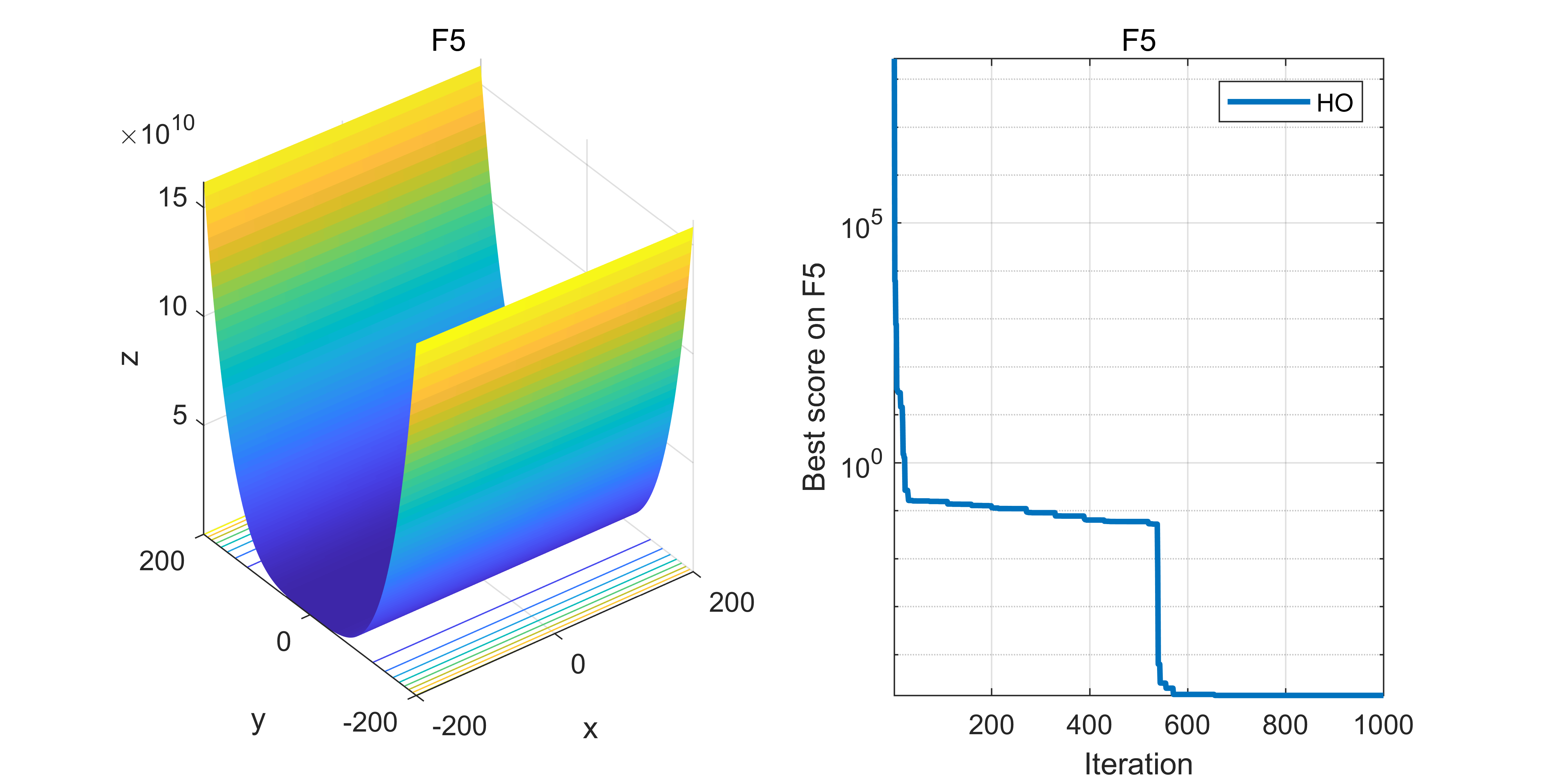
获取代码请关注MATLAB科研小白的个人公众号（即文章下方二维码），并回复：智能优化算法本公众号致力于解决找代码难，写代码怵。各位有什么急需的代码，欢迎后台留言~不定时更新科研技巧类推文，可以一起探讨科研，写作，文献，代码等诸多学术问题，我们一起进步。