Python机器学习--回归算法--逻辑回归算法_python 逻辑回归 标准误差

逻辑回归算法

逻辑回归算法类型:

逻辑回归属于有监督学习的分类算法（只能做二分类）

逻辑回归算法原理:

将线性回归的结果输入sigmoid函数中，得出预测为类1的概率（
如果概率为0.2 有20%的可能属于类1，属于类0的概率是80%； 结果是类0
如果概率为0.8 有80%的可能属于类1，属于类0的概率是20%； 结果是类1
）
线性回归算法方程

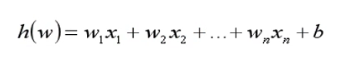
sigmoid函数公式和图像：


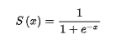
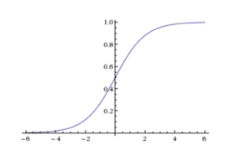
逻辑回归的结果是基于线性回归计算出来的，线性回归的质量好坏会直接影响逻辑回归的结果，影响线性回归的就是回归系数。对于线性回归来说是使用随机梯度下降的方法计算的，对于逻辑回归，也是使用随机梯度下降的方法，只不过将损失函数换成了对数似然损失函数，因为对数似然损失函数中的 h（x）等于sigmoid函数，而sigmoid函数中的x就等于线性回归中的 h(w) ,也就是变相的计算最佳的回归系数。

逻辑回归使用对数似然损失函数来衡量真实结果与预测结果的误差
在对数似然损失函数中通常是以e为底数的
对数似然损失函数公式

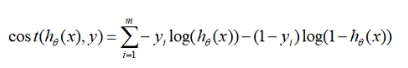
对数似然损失函数计算最佳回归系数的步骤：

• 随机初始化一组【w1,w2,w3,w4…wn】

• 根据初始化的w结合特征值，计算出预测结果sigmoid函数S（x）

• 利用对数似然损失函数，计算出真实值与预测值之间的误差和Loss

• 计算误差关于w的偏导（w等同θ）
  

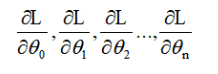
• 沿着梯度的负方向进行更新w（w等同θ）
  
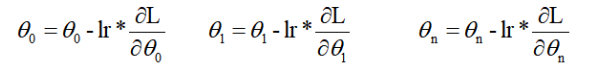
  lr表示的是学习率，lr是小于零的数，意思就是当求出的偏导太大时，减去一个很大的值很容易跳过导数等于0的点，所以要用学习率来控制它梯度下降的幅度。

• 重复2-5步骤，直到达到一定的迭代次数或者损失小于某个值时停止。

逻辑回归基于sklearn的实现

import numpy as np
from sklearn.linear_model import LogisticRegression
# 实例化
alg = LogisticRegression()
# 参数：max_iter:最大迭代次数

# 拟合
alg.fit(X_train, y_train)

# 查看准确率
score = alg.score(X_test, y_test)
print('准确率：', score)

# 查看回归系数
print('回归系数', alg.coef_)
# 查看截距
print('截距：', alg.intercept_)

# 查看sigmoid函数处理过后的概率
prob = 1/(1+np.exp(-alg.decision_function(X_test)))
prob = [float('%.2f'%i) for i in prob]
print('概率：', prob)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

逻辑回归算法的特点

• 结果具有可解释性【可根据线性方程公式可以明确得出结果是如何计算的】
• 只能预测二分类
• 与朴素贝叶斯，knn算法相比，逻辑回归效果更好，但耗时更久。