有环链表环的问题_链表用环的空间复杂度

有关于链表，我们总会遇到关于其的各类问题，像反转链表，双向链表，有环链表等，今天，我们就有环链表展开细说。

---

1.判断链表有环

如果有一个单向链表，且链表中可能出现“环”，那么，该如何用程序来判断该链表是否为有环链表?

方法一：也是最简单粗暴的方法，从头节点开始，依次遍历单链表中的每一个节点。每遍历一次新节点，就与之前所有节点进行比较，如果某个节点被遍历两次，则为有环。(时间复杂度为O(n²),空间复杂度为O(1))。

方法二：创建一个哈希表，以节点的id为key值的哈希表，存储曾经便利过的节点，在依次遍历整个链表，如果遍历的节点为新节点，那就记录在哈希表，当遍历发现在哈希表内部遍历过，证明链表有环。(使用了哈希表作为额外缓存，该解法时间复杂度为O(n),空间复杂度为O(n))。

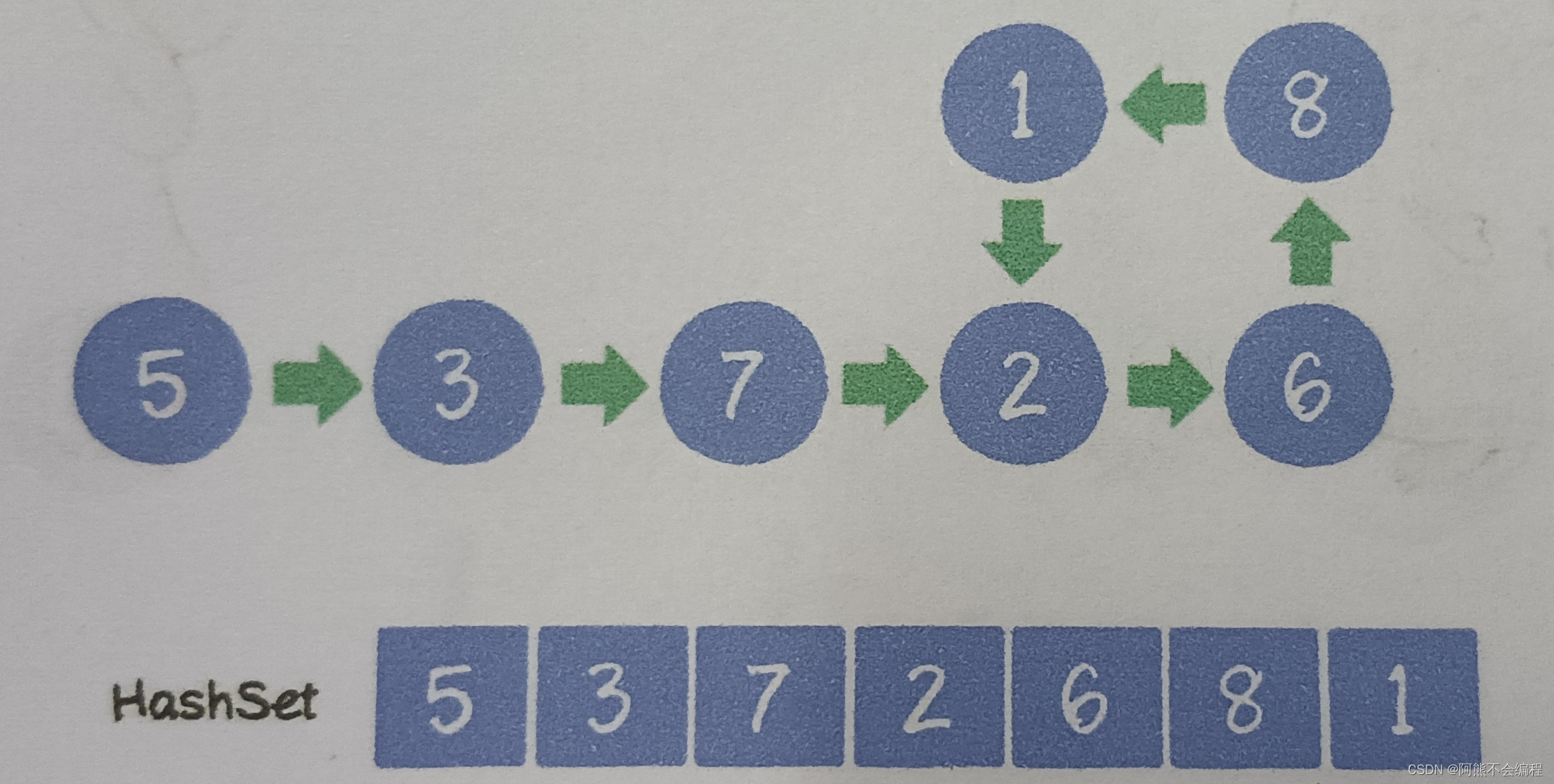
 方法三：利用双指针法.创建两个指针p1,p2使它们同时指向链表的头节点，使p1 = head -> next; p2 = head -> next ->next;(即使p1速度为1，p2速度为2)。

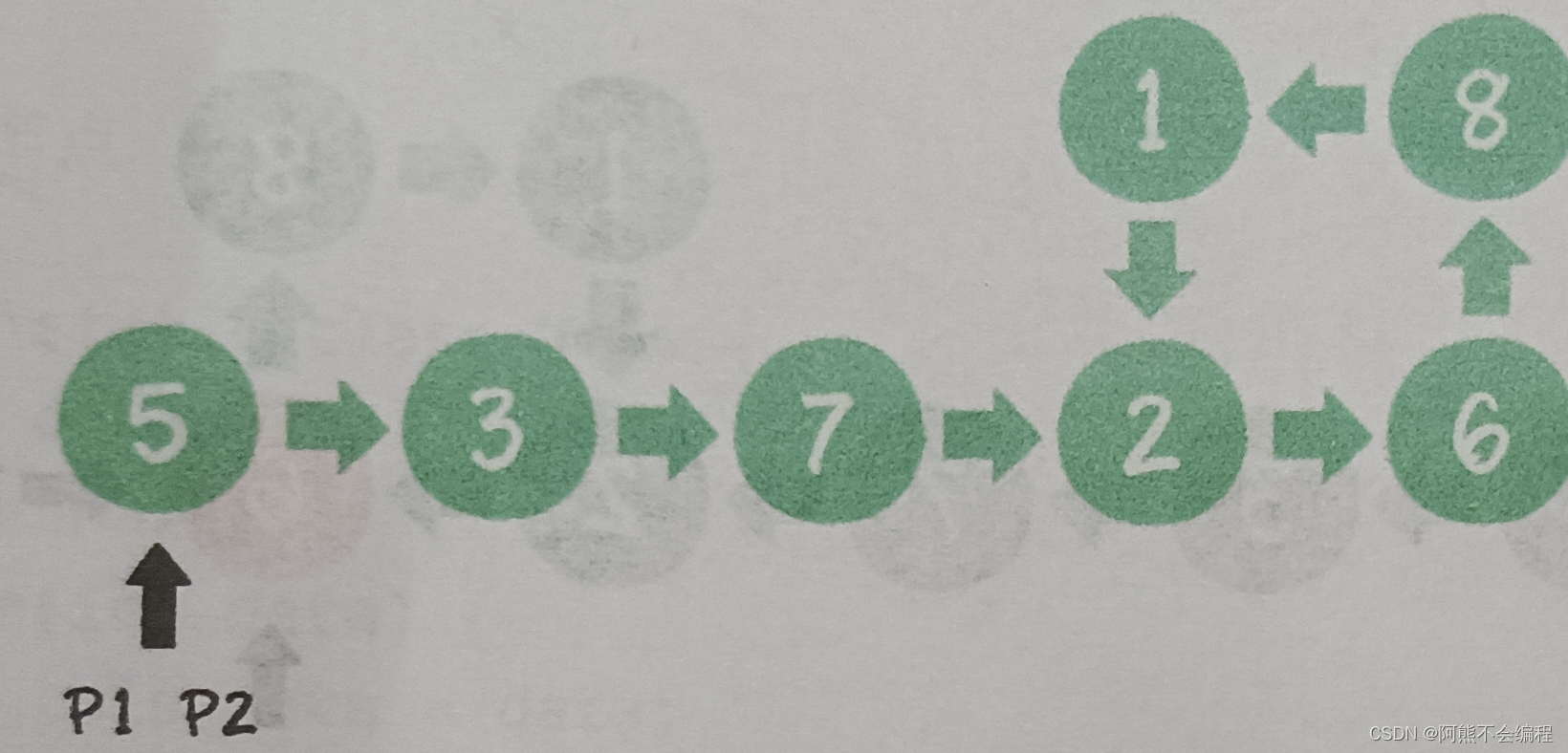
1.p1,p2指向节点5

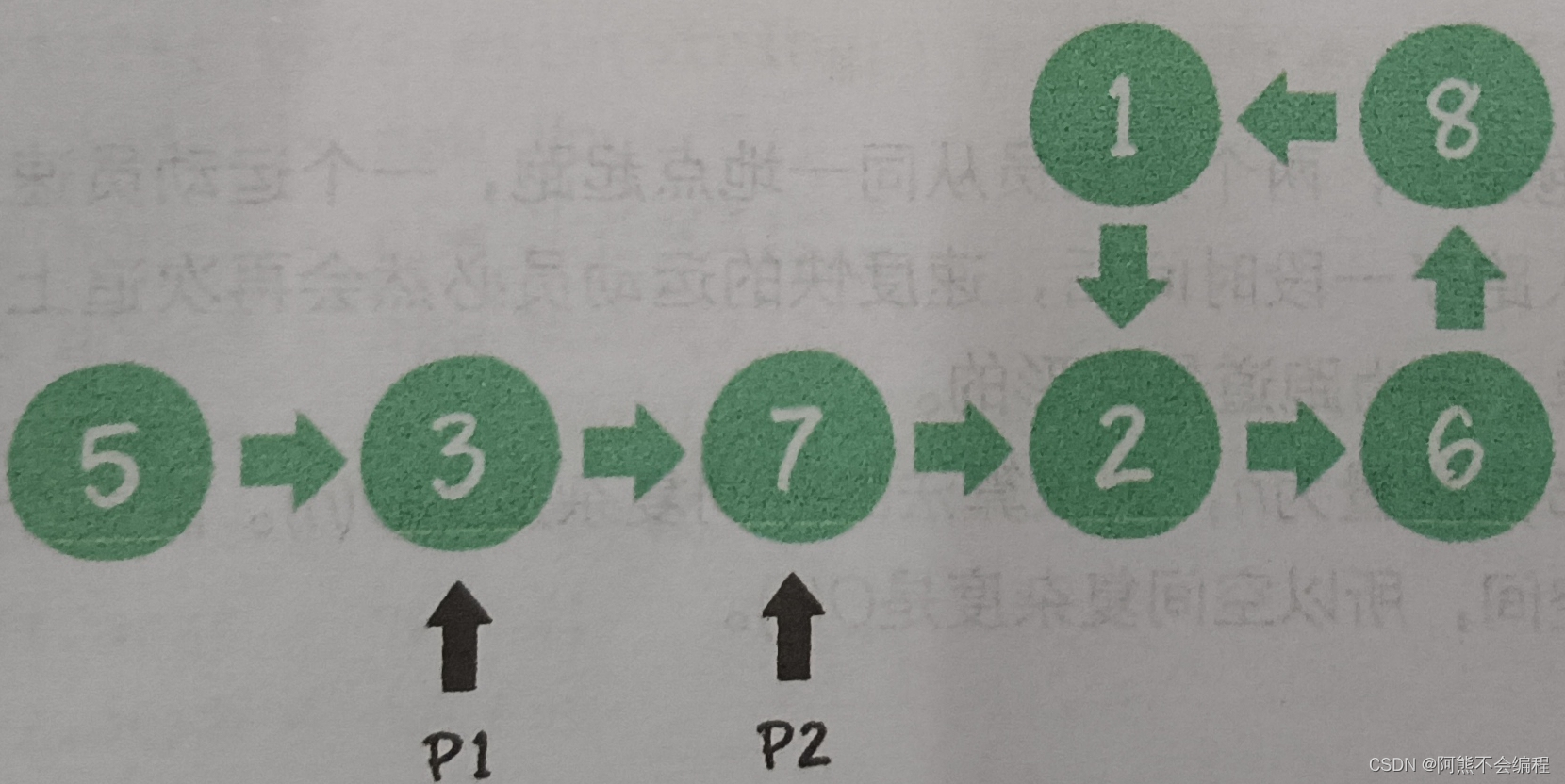
 2.p1指向3，p2指向7

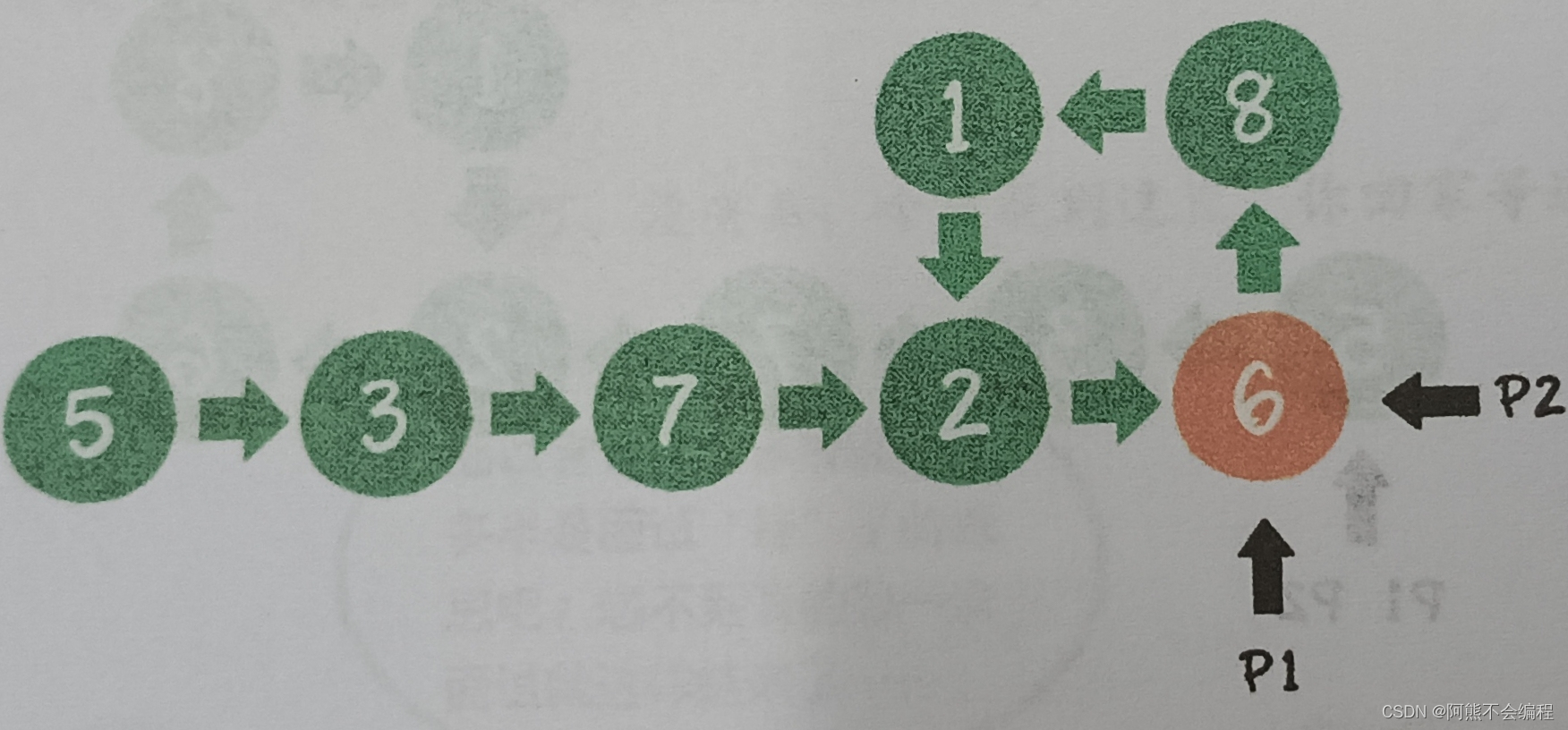
 3.p1保持速度1，p2保持速度2，如果有环，则速度快的一定会追上速度慢的，当p1 == p2时证明了链表有环

下面为部分代码实现：

//部分代码
bool isCycle(ListNode *Head) {
	ListNode* p1 = head;//设置双指针指向头节点
	ListNode* p2 = head;
	while (p2 != NULL && p2->next != NULL)
	{
		p1 = p1->next;//设置p1速度为1
		p2 = p2->next->next;//设置p2速度为2
		if (p1 == p2)
		{
			return ture;//p1 == p2表示两指针相遇，为有环链表
		}
	}
	return false;//双指针不相遇，不是有环链表
}

2.获取有环链表的环长以及入环点

 1.求有环链表的环长

当两个指针首次相遇，证明链表有环的时候，让两个指针从相遇点继续循环前进，统计前进次数，直到第二次相遇，此时统计出来的次数就是环长，因为p1速度为1，p2速度为2，则再次相遇的时候，p2比p1多走了一圈，统计出来前进的次数就为环长。

int isCycle(ListNode *Head) {
	ListNode* p1 = head;
	ListNode* p2 = head;
	static int count = 0;//记录前进次数
	while (p2 != NULL && p2->next != NULL)//第一个循环先使得p1 、 p2 处于第一次相遇的位置
	{
		p1 = p1->next;
		p2 = p2->next->next;
		
		if (p1 == p2)
		{
			break;
		}
	}
	while (p2 != NULL && p2->next != NULL)
	{
		p1 = p1->next;
		p2 = p2->next;
		count++;
		if (p1 == p2)
		{
			break;//第二次相遇时终止循环
		}
	}
	return count;//将记录的前进次数返回
}

 2.求有环链表的入环点

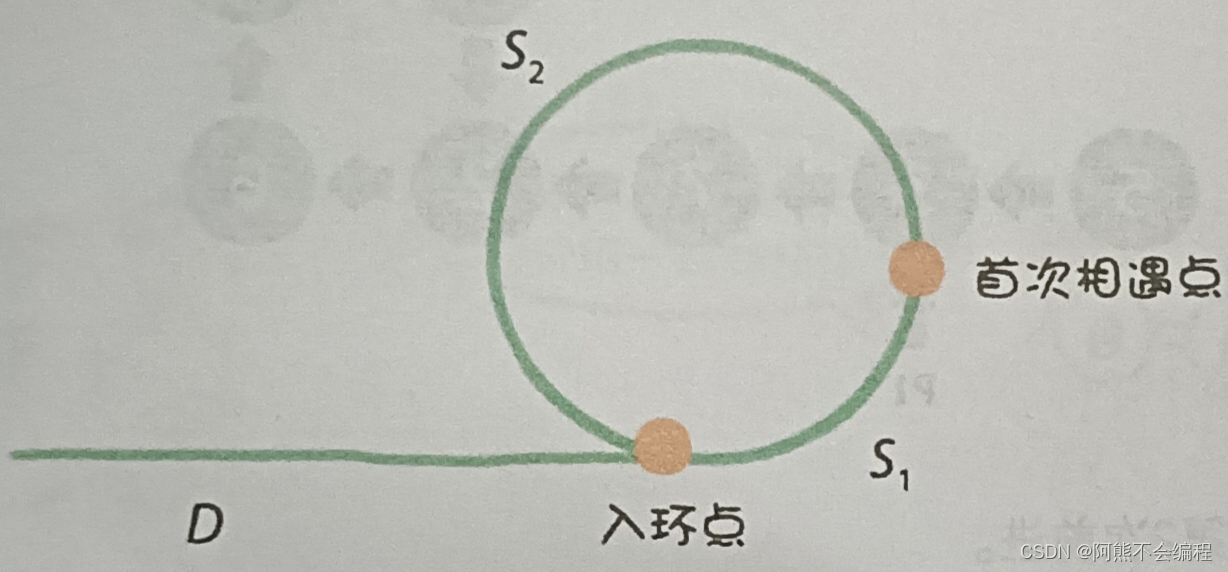
假设从链表头节点到入环点的距离是D，从入环点到两个指针首次相遇点的距离为S1, 从首次相遇点到入环点的距离为S2。

分析：当第一次相遇时，指针P1一次只走一步,  所走的距离为D + S1。指针P2一次走2步， 多走了n(n >= 1) 圈， 所以走的距离为D + S1 + n(S1 + S2)。

则2(D + S1) = D + S1 + n(S1 + S2)

则D = (n - 1)(S1 + S2) + S2

也就是说，从链表头节点到入环点的距离，等于从首次相遇点绕环n - 1 圈在回到入环点的距离

则此时， 把其中任意一个指针放回到头节点，并且保持速度都为1，则他们最终相遇的节点就是入环点。

 

ListNode* detectCycle(ListNode* head) {
	ListNode* p = head, * q = head;
	while (q && q->next) {//当q 与 q 的下一个节点不为空则执行循环
		p = p->next;
		q = q->next->next;
		if (q == p) break;//到达首次相遇点时停止
	}
	if (q == NULL || q->next == NULL) return NULL;
	p = head;
	while (p != q) {//直到再次相遇时停止循环
		p = p->next;
		q = q->next;
	}
	return p;//返回p或q节点都是入环节点
}

---

OK,有环链表的问题今天就介绍到这里啦，主要对有环链表的入环点，环长，以及判断是否存在环（前两个例子我就不敲了，理解就好）希望对你有所帮助，学无止境，我们一起加油一起学习，也祝各位小伙伴们学业有成，早日进入自己心仪的大厂！