learning rate_学习率大小对训练的影响

1. 学习率对训练的影响

为了能够使得梯度下降法有较好的性能，我们需要把学习率的值设定在合适的范围内。太大的学习速率导致学习的不稳定，太小值又导致极长的训练时间。自适应学习速率通过保证稳定训练的前提下，达到了合理的高速率，可以减少训练时间。

2. 学习率的设置

固定学习率的设置：

1. 经验选择：一般情况下倾向于选取较小的学习速率以保证系统的稳定性，学习速率的选取范围在0.01~0.8之间。
2. 对于不同大小的数据集，调节不同的学习率。根据我们选择的成本函数F()不同，问题会有区别。当平方误差和（Sum of Squared Errors）作为成本函数时， ∂F(ωj) / ∂ωj 会随着训练集数据的增多变得越来越大，因此学习率需要被设定在相应更小的值上。解决此类问题的一个方法是将学习率λ 乘上1/N，N是训练集中数据量。这样每步更新的公式变成下面的形式：ωj = ωj - (λ/N) * ∂F(ωj) / ∂ωj 
   解析：固定学习率是根据cost曲线的走向来不断调整学习率，最终获得比较好的初始化。其往往搭配Early Stopping来结束训练。

可变的学习率：

1. 在每次迭代中调节不同的学习率。在每次迭代中去调整学习率的值是另一种很好的学习率自适应方法。此类方法的基本思路是当你离最优值越远，你需要朝最优值移动的就越多，即学习率就应该越大；反之亦反。例如：如果相对于上一次迭代，错误率减少了，就可以增大学习率，以5%的幅度；如果相对于上一次迭代，错误率增大了（意味着跳过了最优值），那么应该重新设置上一轮迭代ωj 的值，并且减少学习率到之前的50%。
2. 当validation accuracy满足early stopping时，但是我们可以不stop，而是让learning rate减半之后让程序继续跑。下一次validation accuracy又满足no-improvement-in-n规则时，我们同样再将learning rate减半。继续这个过程，直到learning rate变为原来的1/1024再终止程序。（1/1024还是1/512还是其他可以根据实际确定）。

关于调节学习率的几点建议

1.对于不同大小的数据集，调节不同的学习率

根据我们选择的成本函数F(x)不同，问题会有区别。当平方误差和（Sum of Squared Errors）作为成本函数时， 会随着训练集数据的增多变得越来越大，因此学习率需要被设定在相应更小的值上。 
解决此类问题的一个方法是将学习率λ 乘上1/N，N是训练集中数据量。这样每步更新的公式变成下面的形式： 

相关内容可参考： Wilson et al. paper “The general inefficiency of batch training for gradient descent learning”

另外一种解决方法是：选择一个不被训练集样本个数影响的成本函数，如均值平方差（Mean Squared Errors）。

2. 在每次迭代中调节不同的学习率

在每次迭代中去调整学习率的值是另一种很好的学习率自适应方法。此类方法的基本思路是当你离最优值越远，你需要朝最优值移动的就越多，即学习率就应该越大；反之亦然。

但是这里有一个问题，就是我们并不知道实际上的最优值在哪里，我们也不知道每一步迭代中我们离最优值有多远。 
解决办法是，我们在每次迭代的最后，使用估计的模型参数检查误差函数（error function）的值。如果相对于上一次迭代，错误率减少了，就可以增大学习率，以5%的幅度；如果相对于上一次迭代，错误率增大了（意味着跳过了最优值），那么应该重新设置上一轮迭代ωj 的值，并且减少学习率到之前的50%。这种方法叫做 Bold Driver.

3. 建议：归一化输入向量

归一化输入向量在机器学习问题中是一个通用的方法。在一些应用中，由于使用距离或者特征方差，要求必须归一化输入向量，因为如果不归一化将导致结果会严重被具有大方差的特征和不同的尺度影响。归一化输入能够帮助数值最优方法（例如，梯度下降法）更快，更准确地收敛。

尽管有一些不同的归一化变量的方法，[0,1]归一化（也叫做min-max）和z-score归一化是两种最为广泛应用的。

学习率是深度学习中的一个重要的超参，如何调整学习率是训练出好模型的关键要素之一。在通过SGD求解问题的极小值时，梯度不能太大，也不能太小。太大容易出现超调现象，即在极值点两端不断发散，或是剧烈震荡，总之随着迭代次数增大loss没有减小的趋势；太小会导致无法快速地找到好的下降的方向，随着迭代次数增大loss基本不变。

因此，我们常常用一些退火的方法调整学习率。学习率调整方法基本上有两种

1. 基于经验的手动调整。 通过尝试不同的固定学习率，如0.1, 0.01, 0.001等，观察迭代次数和loss的变化关系，找到loss下降最快关系对应的学习率。

2. 基于策略的调整。

   2.1 fixed 、exponential、polynomial

   2.2. 自适应动态调整。adadelta、adagrad、ftrl、momentum、rmsprop、sgd

关于学习率的大小

学习率是深度学习中的一个重要的超参，如何调整学习率是训练出好模型的关键要素之一。在通过SGD求解问题的极小值时，梯度不能太大，也不能太小。太大容易出现超调现象，即在极值点两端不断发散，或是剧烈震荡，总之随着迭代次数增大loss没有减小的趋势；太小会导致无法快速地找到好的下降的方向，随着迭代次数增大loss基本不变。

因此，我们常常用一些退火的方法调整学习率。学习率调整方法基本上有两种

1. 基于经验的手动调整。 通过尝试不同的固定学习率，如0.1, 0.01, 0.001等，观察迭代次数和loss的变化关系，找到loss下降最快关系对应的学习率。

2. 基于策略的调整。

   2.1 fixed 、exponential、polynomial

   2.2. 自适应动态调整。adadelta、adagrad、ftrl、momentum、rmsprop、sgd

学习率 (learning rate)，控制 模型的 学习进度 ： 

lr 即 stride (步长) ，即反向传播算法中的  ：

学习率大小

学习率设置

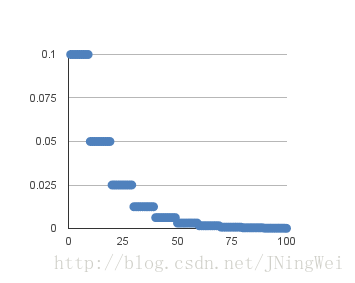
在训练过程中，一般根据训练轮数设置动态变化的学习率。

• 刚开始训练时：学习率以 0.01 ~ 0.001 为宜。
• 一定轮数过后：逐渐减缓。
• 接近训练结束：学习速率的衰减应该在100倍以上。

Note： 
如果是 迁移学习 ，由于模型已在原始数据上收敛，此时应设置较小学习率 () 在新数据上进行 微调 。

学习率减缓机制

把脉 目标函数损失值 曲线

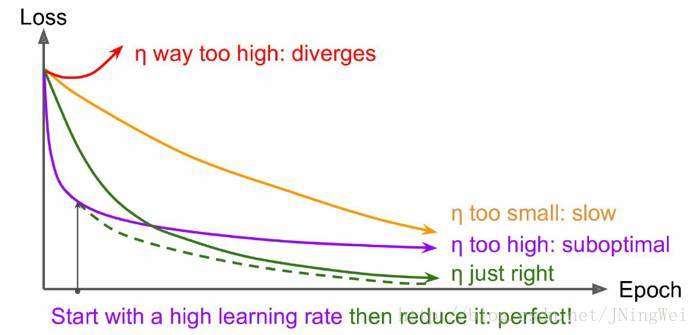
理想情况下 曲线 应该是 滑梯式下降 [绿线]： 

1. 曲线 初始时 上扬 [红线]： 
   Solution：初始 学习率过大 导致 振荡，应减小学习率，并 从头 开始训练 。
2. 曲线 初始时 强势下降 没多久 归于水平 [紫线]： 
   Solution：后期 学习率过大 导致 无法拟合，应减小学习率，并 重新训练 后几轮 。
3. 曲线 全程缓慢 [黄线]： 
   Solution：初始 学习率过小 导致 收敛慢，应增大学习率，并 从头 开始训练 。