探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（五）RMS 均方根归一化

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（五）RMS 均方根归一化

RMS（均方根归一化）

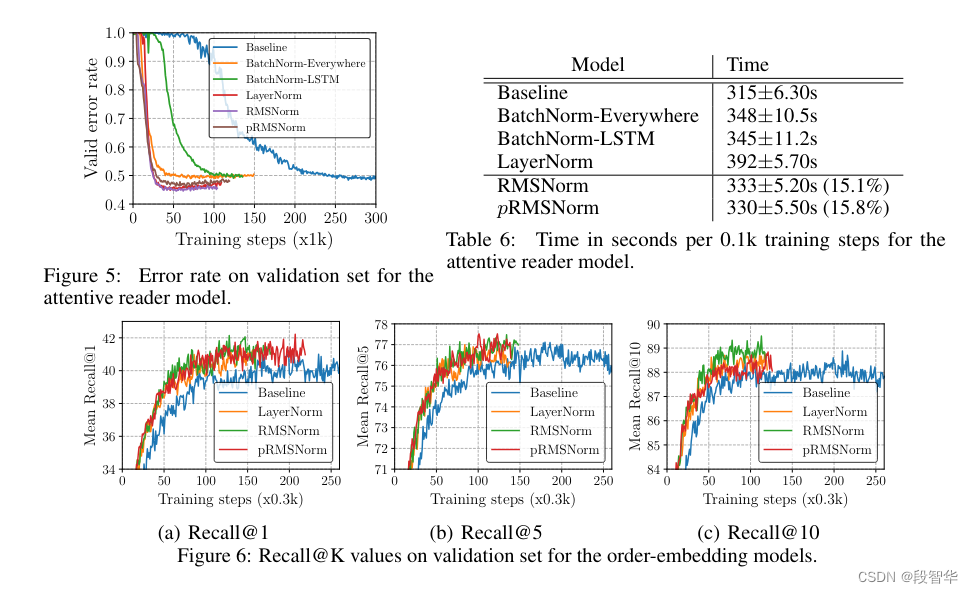
均方根归一化（RMSNorm）是一种相对新颖的归一化技术，由 Biao Zhu、Rico Sennrich 在 2019 年提出。与 BN 和 LN 不同，RMSNorm 基于激活本身的均方根对激活进行归一化，而不是使用小批量或层统计数据。这种方法可确保无论小批量大小或特征数量如何，激活的缩放都是一致的。此外，RMSNorm 引入了可学习的尺度参数，提供与批量归一化类似的适应性。

像层归一化一样， 也有一个可学习的参数gamma（左侧公式中的g ），它乘以归一化值。

class RMSNorm(nn.Module):
    def __init__(self, dim: int, eps: float = 1e-5):
        super().__init__()
        self.eps = eps
        # The gamma parameter
        self.weight = nn.Parameter(torch.ones(dim))

    def _norm(self, x: torch.Tensor):
        # (B, seq_len, dim) -> (B, seq_len, 1)
        return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)

    def forward(self, x: torch.Tensor):
        # dim : (B, seq_len, dim) -> (B, seq_len, dim)
        return self.weight * self._norm(x.float()).type_as(x)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

系列博客

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（一）
https://duanzhihua.blog.csdn.net/article/details/138208650
探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（二）
https://duanzhihua.blog.csdn.net/article/details/138212328

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（三）KV缓存
https://duanzhihua.blog.csdn.net/article/details/138213306

探索和构建 LLaMA 3 架构：深入探讨组件、编码和推理技术（四）分组多查询注意力
https://duanzhihua.blog.csdn.net/article/details/138216050