数据结构—队列（C语言实现）

---

前言

嗨喽喽！！小伙伴们，大家好哇，欢迎来到我的博客！

今天将要分享的是另一种数据结构—队列，以及与队列具有相通之处的一种结构，循环队列的实现。

一、队列的概念

队列（Queue）：只能在一端进行插入数据操作，在另一端进行删除数据的特殊线性表。与栈相反的是，队列遵循先进先出 FIFO(First In First Out)的原则，进行插入数据的一端称之为队尾（入队），进行删除数据的一端则为队头（出队）。

看到队列这一数据结构的名字与以上对于队列的概念的说明，相信小伙伴们脑海中早已浮现日常生活中与此结构相类似的场景。就是我们平时购买物品或办理业务时，通常会采取排队的方式确保秩序与公平，先入队的人先出队。

二、队列的实现

讲述完了队列的相关概念，接下来便可以着手实现队列及其有关的基本操作了！！
队列既可以使用数组也可以使用链表来实现。但是总体来说，使用链表实现更优，因为使用数组在队头出数据，其效率会低很多。

所以我们使用链表来实现一个队列：

Queue.h

首先时队列头文件的头文件包含与链表和队列的声明：

typedef int QDataType;

typedef struct QListNode
{
	struct QListNode* _pNext;//指向队列的下一个
	QDataType _data;
}QNode;

typedef struct Queue
{
	QNode* _front;//指向队头
	QNode* _rear;//指向队尾
	int _size;
}Queue;
1
2
3
4
5
6
7
8
9
10
11
12
13
14

然后是，队列中的一些相关的方法的声明：

//初始化队列
void QueueInit(Queue* q);
//销毁队列
void QueueDestroy(Queue* q);

//入队(队尾)
void QueuePush(Queue* q, QDataType x);
//出队(队头)
void QueuePop(Queue* q);

//获取队头元素
QDataType QueueFront(Queue* q);
//获取队尾元素
QDataType QueueBack(Queue* q);

//队列判空
bool QueueEmpty(Queue* q);
//获取队列元素个数
int QueueSize(Queue* q);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Queue.c

接下来便是队列中的一些方法的实现：
首先是队列的初始化与销毁，销毁操作类似于链表，通过遍历对节点逐个释放：

void QueueInit(Queue* q)
{
	assert(q);
	q->_front = q->_rear = NULL;
	q->_size = 0;
}

void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* pcur, * next;
	pcur = q->_front;
	while (pcur)
	{
		next = pcur->_pNext;
		free(pcur);
		pcur = next;
	}
	q->_front = q->_rear = NULL;
	q->_size = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

然后是队列的入队操作，在入队之前需要先检查队列是否为空：

void QueuePush(Queue* q, QDataType x)
{
	assert(q);
	QNode* node = (QNode*)malloc(sizeof(QNode));
	if (node == NULL)
	{
		perror("malloc fail！");
		exit(1);
	}
	node->_data = x;
	node->_pNext = NULL;
	if (q->_rear)//队列不为空
	{
		q->_rear->_pNext = node;
	}
	else//队列为空
	{
		q->_front = node;
	}
	q->_rear = node;
	q->_size++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

使用动画解释入队操作：

然后是出队操作，此处则存在队列为一个元素与多个元素的情况：

void QueuePop(Queue* q)
{
	assert(q && q->_size);
	if (q->_front->_pNext)//队列不仅一个元素
	{
		QNode* next = q->_front->_pNext;
		free(q->_front);
		q->_front = NULL;
		q->_front = next;
	}
	else//队列仅一个元素
	{
		free(q->_front);
		q->_front = q->_rear = NULL;
	}
	q->_size--;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

使用动画解释出队操作：

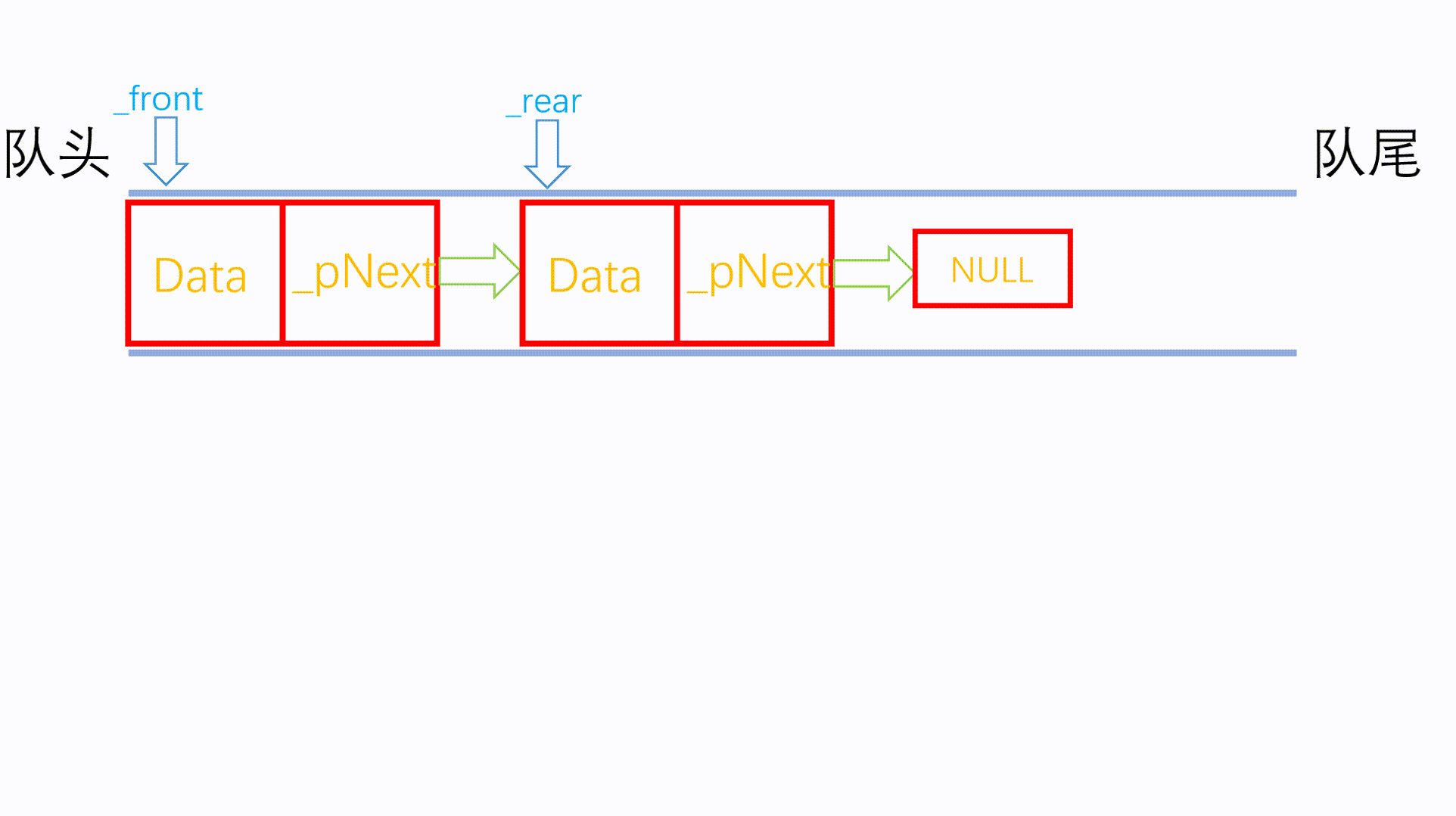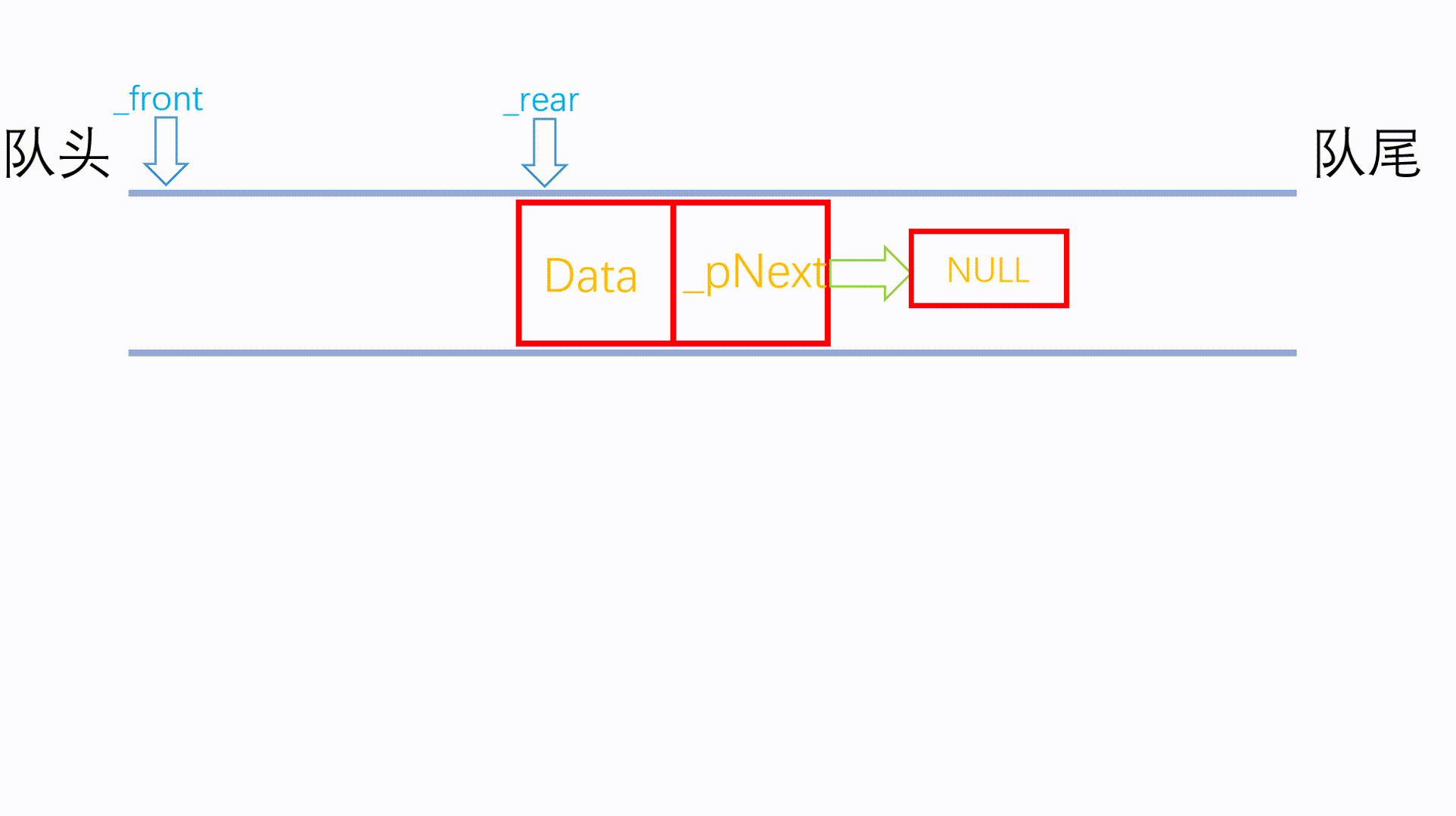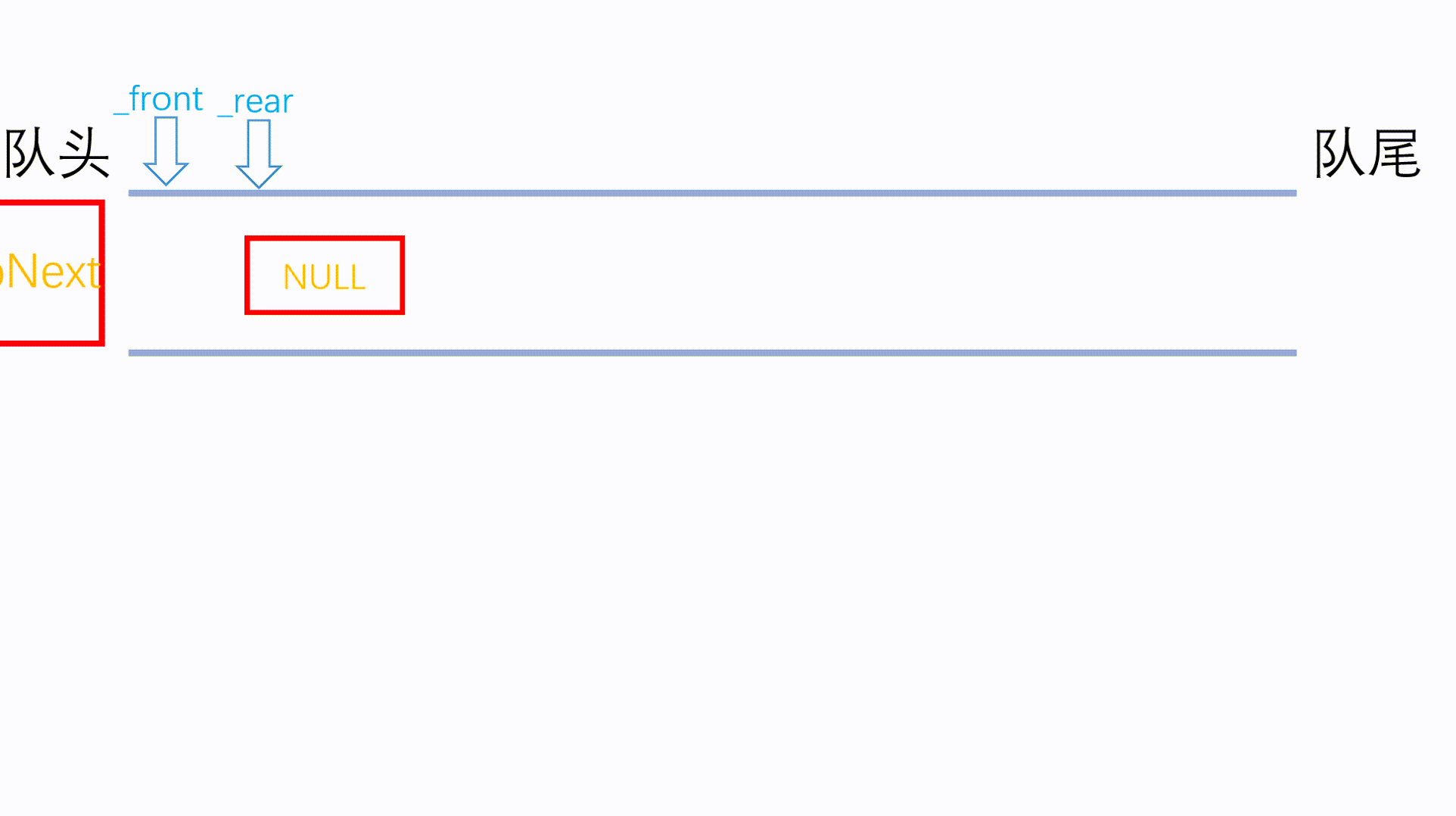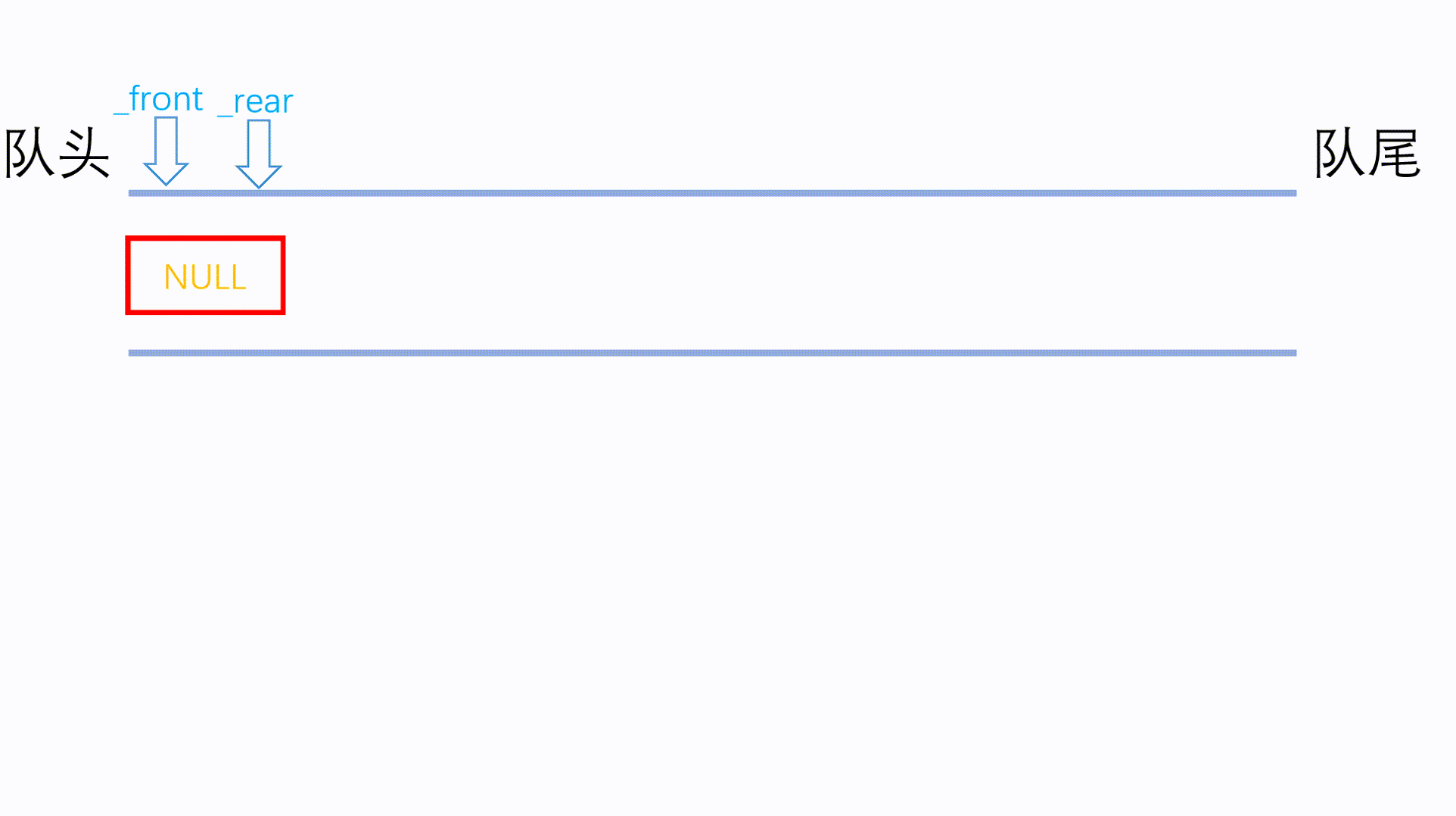
然后是获取队头与队尾元素：

QDataType QueueFront(Queue* q)
{
	assert(q && q->_front);
	return q->_front->_data;
}

QDataType QueueBack(Queue* q)
{
	assert(q && q->_rear);
	return q->_rear->_data;
}
1
2
3
4
5
6
7
8
9
10
11

最后则是队列的判空与获取当前队列的大小的操作：

bool QueueEmpty(Queue* q)
{
	assert(q);
	return q->_size == 0;
}

int QueueSize(Queue* q)
{
	assert(q);
	return q->_size;
}
1
2
3
4
5
6
7
8
9
10
11

三、设计循环队列问题

分享完了队列的相关内容，接下来让我们看一个与队列有一定相通之处的设计循环队列的问题。
首先给出力扣上的相关题目的链接：【设计循环队列】。

当然，这个循环队列既可以使用数组也可以使用链表来实现，由于难度基本相差不大。这边主要使用数组来讲解实现过程，同时在最后也会给出使用链表实现的相关代码。

数组实现

首先通过题目我们可以知道循环队列的逻辑结构大致类似于下图：

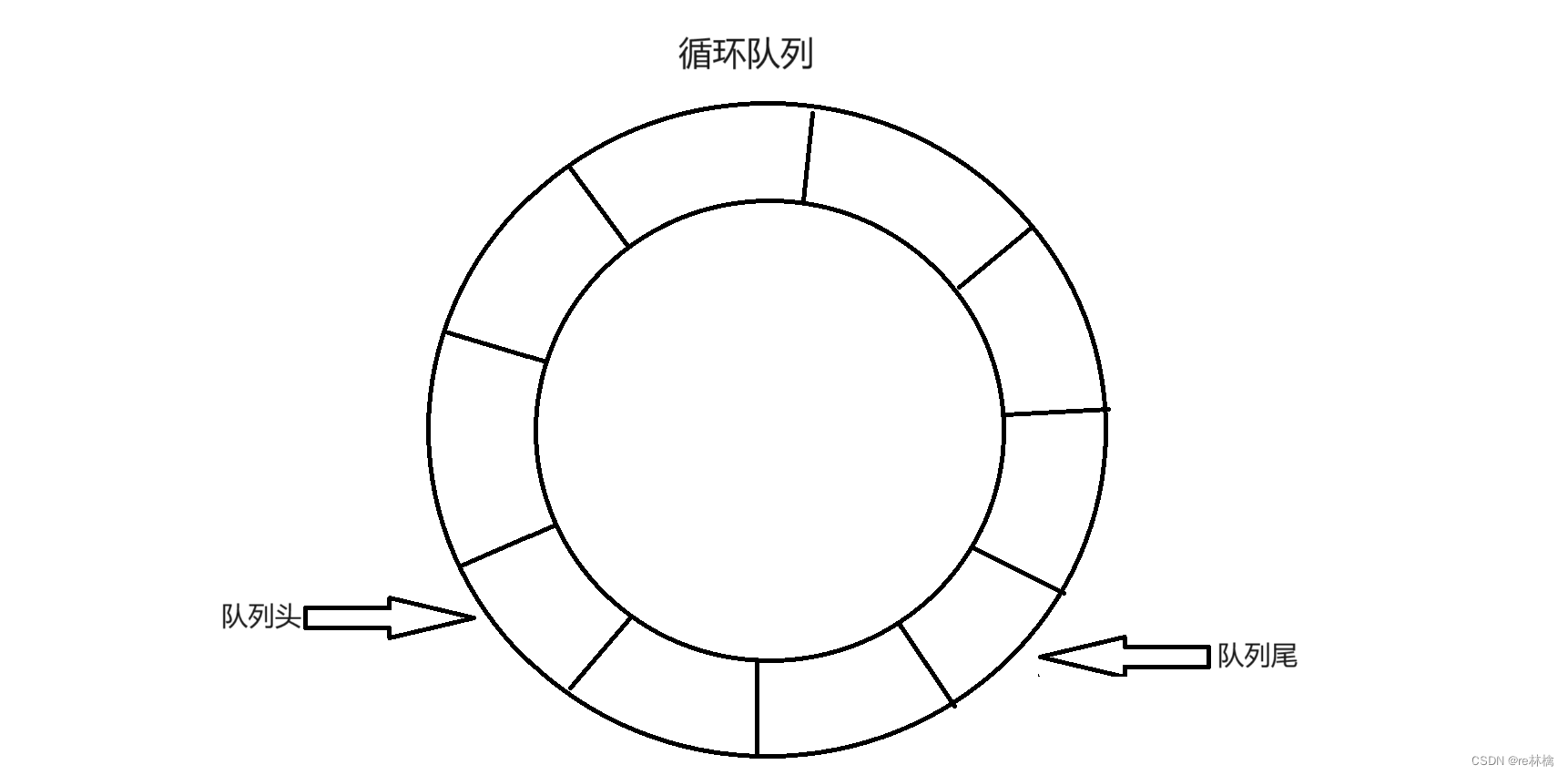
但是他的物理结构上确实一个数组，不可能将首尾相接。那么这里我们便可以通过对tail用size取模。当tail在数组末尾时再加一，那么肯定会造成数组越界，此时我们就可以使用size对tail进行取模，tail便成了0，指向了数组首位，如此便形成了循环，当然队头也可以使用相类似的操作。如下图所示，tail开始为5，size为6，此时队列入数据，对tail加1，我们对tail取模，tail就等于了0：

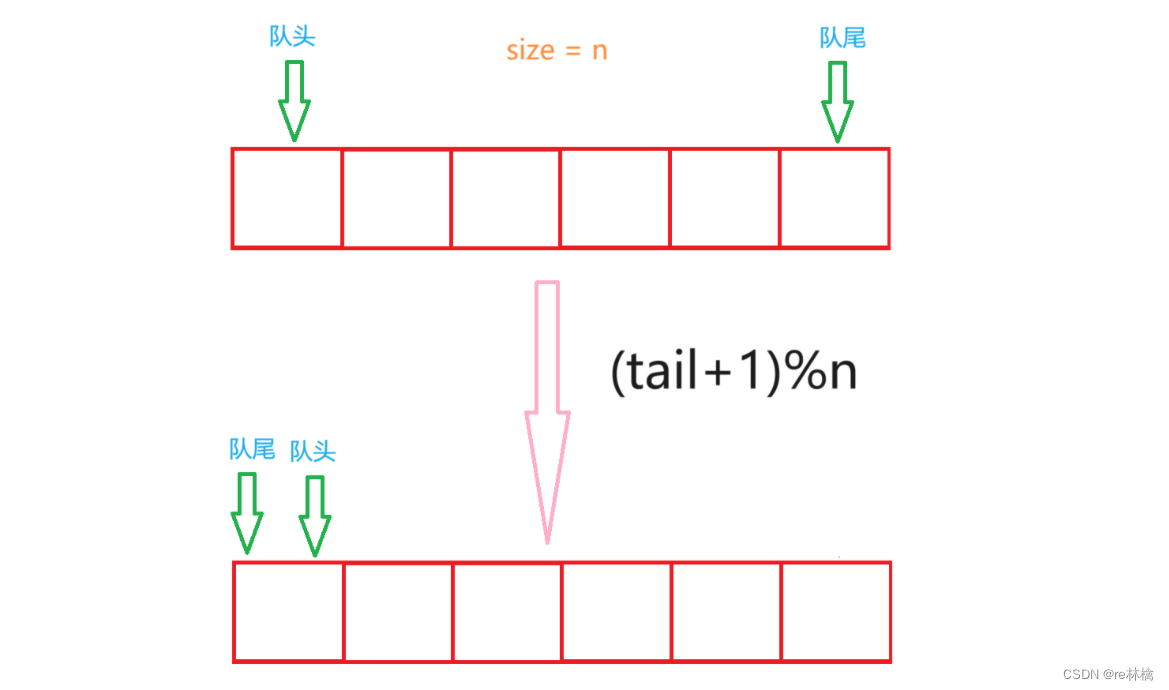
但此时，我们会存在两种特殊情况，那便是数组的空与满。数组为空还可以放入元素，为满那肯定不可以再存入元素。这时，可能部分小伙伴会说，判断此时队头与队尾指向的位置是否相同，来区分空与满。但要知道的是空与满时队头与队尾指向的位置其实都是相同的。

其实此时我们可以采取两种方法来解决上述的问题：
1、使用一个size来记录当前的数组元素的个数，当元素的个数与循环队列的长度k相等时，不就为满了，size==0不就为空了。

2、我们可以实际上创建k+1个长度循环队列，然后让tail一直指向末尾元素的下一个下标的位置，即让数组中始终有一个位置不存放数据。此时队头与队尾指向同一个位置时，即为空；队尾的下一个为队头就为满:

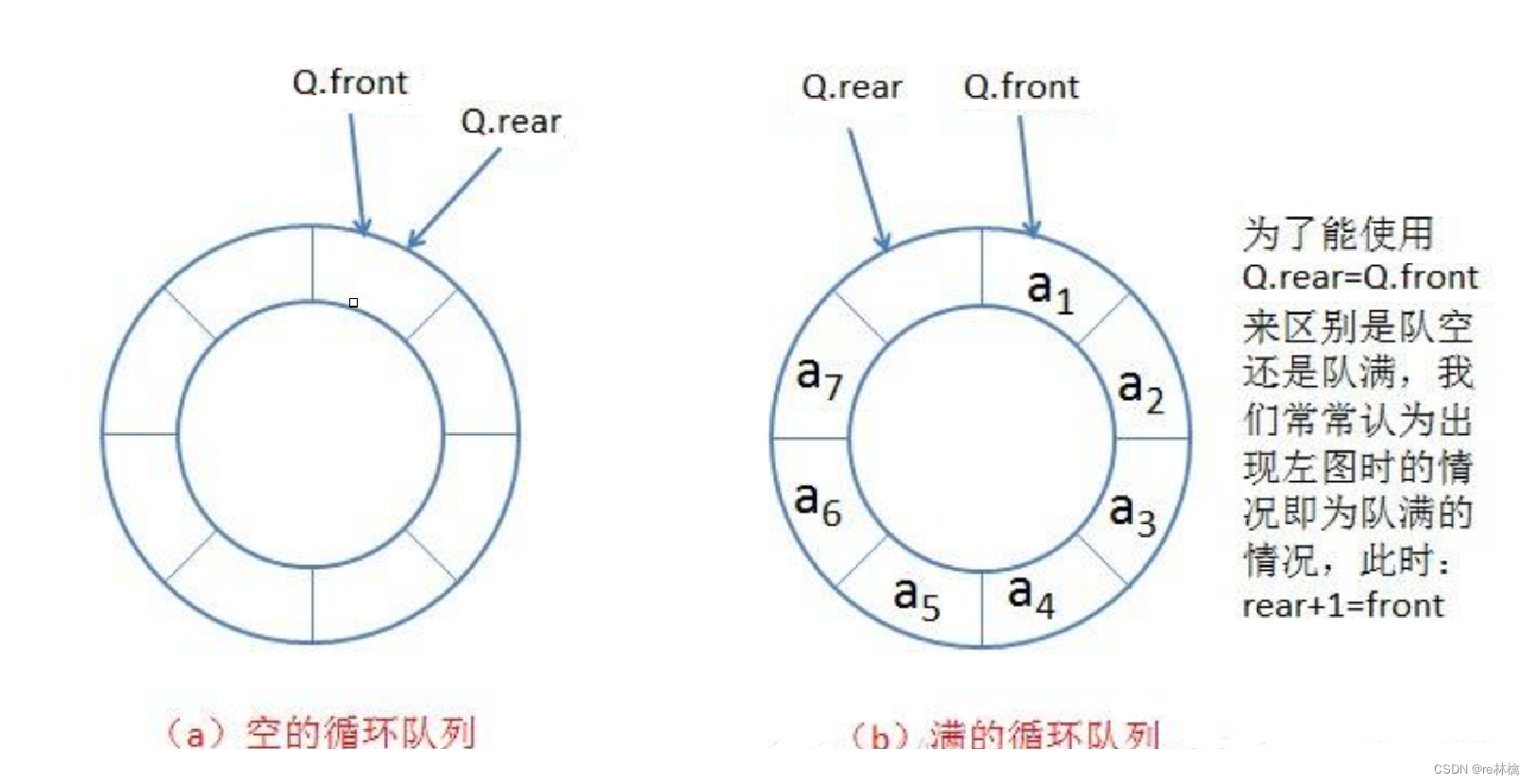
那我们就使用第一种方法来手撕一个循环队列吧！！
首先是循环队列的声明：

typedef struct {
    int* a;
    int head;
    int tail;
    int size;//判断满与空的特殊情况
    int k;
} MyCircularQueue;
1
2
3
4
5
6
7

然后是循环队列的初始化，一开始头与尾都指向数组的开始位置：

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* pcq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    pcq->a = (int*)malloc(k * sizeof(int));
    pcq->size = pcq->head = pcq->tail = 0;
    pcq->k = k;
    return pcq;
}
1
2
3
4
5
6
7

循环队列的入队操作，入队之前需要先判断队列是否为满，即size与k相等时即为满，然后在对tial加加了之后，则需要使用k对tail取模，形成循环：

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (obj->size == obj->k)//循环队列为满
    {
        return false;
    }
    obj->a[obj->tail] = value;
    obj->tail++;
    obj->tail %= obj->k;
    obj->size++;
    return true;
}
1
2
3
4
5
6
7
8
9
10
11

循环队列的出队操作，出队之前则需要判断队列是否为空（即size==0），不为空，就直接让head++。同样的，在对head++后也需要使用k对head进行取模操作：

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if (obj->size == 0)//循环队列为空
    {
        return false;
    }
    obj->head++;
    obj->head %= obj->k;
    obj->size--;
    return true;
}
1
2
3
4
5
6
7
8
9
10

然后是循环队列的取队头数据的操作，直接返回head指向的数据即可：

int myCircularQueueFront(MyCircularQueue* obj) {
    if (obj->size == 0)
        return -1;
    return obj->a[obj->head];
}
1
2
3
4
5

取循环队列的尾数据就相对复杂了，因为tail的前一个元素为尾元素。那么，当tail==0时，尾元素在数组的末尾位置。当然，有一种简单的解决方法：使用三目运算符，即判断tail是否指向0，是就返回数组末尾元素（即k - 1的位置），否就只返回tail - 1指向的元素即可。
此处同时还有一种更为