算法数据结构基础——图（Graph）_graph 算法

1. 图的定义

图（Graph）：由顶点的非空有限集合 $V$ （由 $n > 0$ 个顶点组成）与边的集合 $E$（顶点之间的关系）构成的结构。其形式化定义为 $G = (V, E)$。

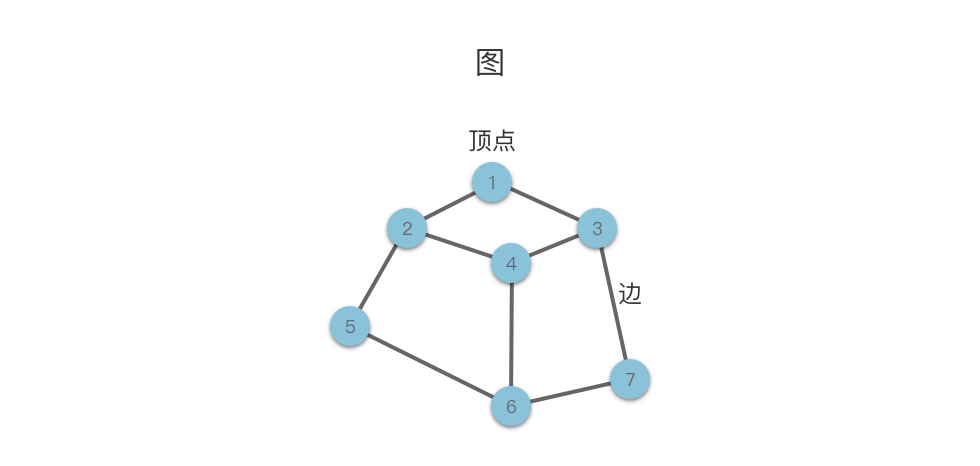
• 顶点（Vertex）：图中的数据元素通常称为顶点，在下面的示意图中我们使用圆圈来表示顶点。

• 边（Edge）：图中两个数据元素之间的关联关系通常称为边，在下面的示意图中我们使用连接两个顶点之间的线段来表示边。边的形式化定义为：$e = \langle u, v \rangle$，表示从 $u$ 到 $v$ 的一条边，其中 $u$ 称为起始点，$v$ 称为终止点。

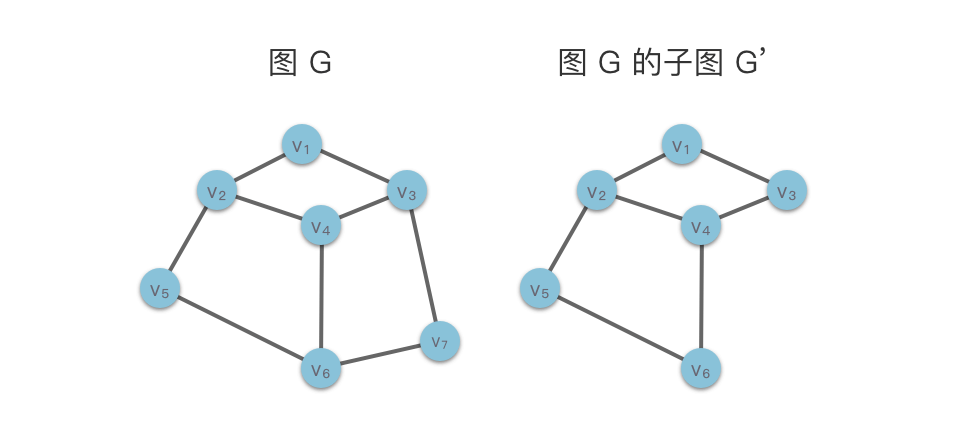
• 子图（Sub Graph）：对于图 $G = (V, E)$ 与 $G^{'} = (V^{'}, E^{'})$，如果存在 $V^{'} \subseteq V$，$E^{'} \subseteq E$，则称图 $G^{'}$ 是图 $G$ 的一个子图。在下面的示意图中我们给出了一个图 $G$ 及其一个子图 $G^{'}$。特别的，根据定义，$G$ 也是其自身的子图。

2. 图的分类

2.1 无向图和有向图

按照边是否有方向，我们可以将图分为两种类型：「无向图」和「有向图」。

• 无向图（Undirected Graph）：如果图中的每条边都没有指向性，则称为无向图。例如朋友关系图、路线图都是无向图。

• 有向图（Directed Graph）：如果图中的每条边都具有指向性，则称为有向图。例如流程图是有向图。

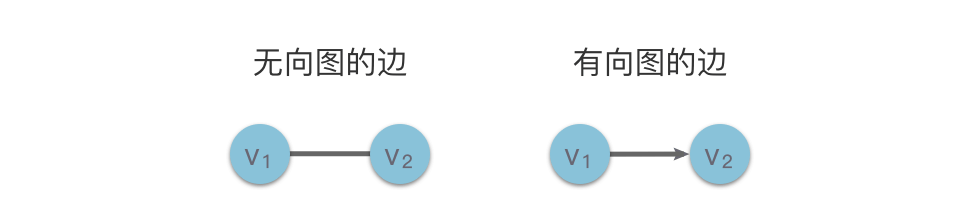
在无向图中，每条边都是由两个顶点组成的无序对。例如下图左侧中的顶点 $v_1$ 和顶点 $v_2$ 之间的边记为 $(v_1, v_2)$ 或 $(v_2, v_1)$。

在有向图中，有向边也被称为弧，每条弧是由两个顶点组成的有序对，例如下图右侧中从顶点 $v_1$ 到顶点 $v_2$ 的弧，记为 $\langle v_1, v_2 \rangle$，$v_1$ 被称为弧尾，$v_2$ 被称为弧头，如下图所示。

如果无向图中有 $n$ 个顶点，则无向图中最多有 $n * (n - 1) / 2$ 条边。而具有 $n * (n - 1) / 2$ 条边的无向图称为 「完全无向图（Completed Undirected Graph）」。

如果有向图中有 $n$ 个顶点，则有向图中最多有 $n * (n - 1)$ 条弧。而具有 $n * (n - 1)$ 条弧的有向图称为 「完全有向图（Completed Directed Graph）」。

如下图所示，左侧为包含 4 个顶点的完全无向图，右侧为包含 4 个顶点的完全有向图。

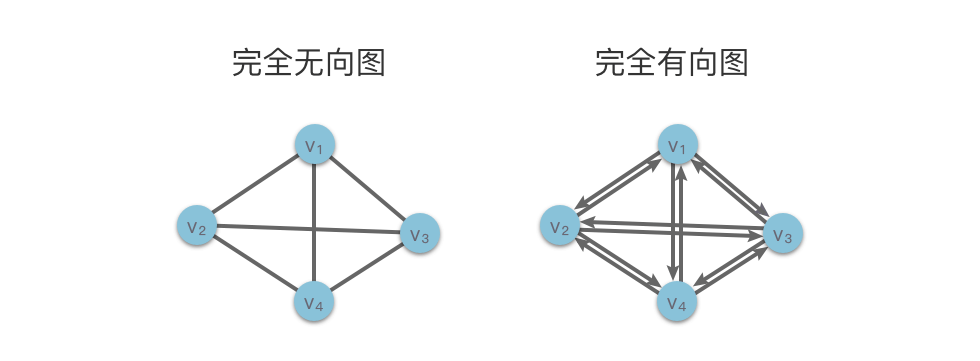
下面介绍一下无向图和有向图中一个重要概念 「顶点的度」。

• 顶点的度：与该顶点 $v_i$ 相关联的边的条数，记为 $TD(v_i)$。

例如上图左侧的完全无向图中，顶点 $v_3$ 的度为 3。

而对于有向图，我们可以将顶点的度分为 「顶点的出度」 和 「顶点的入度」。

• 顶点的出度：以该顶点 $v_i$ 为出发点的边的条数，记为 $OD(v_i)$。

• 顶点的入度：以该顶点 $v_i$ 为终止点的边的条数，记为 $ID(v_i)$。

• 有向图中某顶点的度 = 该顶点的出度 + 该顶点的入度，即 $TD(v_i) = OD(v_i) + ID(v_i)$。

例如上图右侧的完全有向图中，顶点 $v_3$ 的出度为 3，入度为 3，顶点 $v_3$ 的度为 3 + 3 = 6。

2.2 环形图和无环图

「路径」 是图中的一个重要概念，对于图 $G = (V, E)$，如果存在顶点序列 $v{i_0}, v{i_1}, v{i_2},… , v{i_m}$，使得 $(v{i_0}, v{i_1})，(v{i_1}, v{i_2})，…，(v{i{m-1}}, v{i_m}) \in E$（即他们都是图 G 的边，对于有向图则是 $\langle v{i_0}, v{i_1} \rangle，\langle v{i_1}, v{i_2} \rangle，…，\langle v{i{m-1}}, v{i_m} \rangle \in E$），则称该顶点序列为顶点 $v{i_0}$ 和顶点 $v{i_m}$ 之间的一条路径，其中 $v{i_0}$ 是这条路径的起始点，$v{i_m}$ 是这条路径的终止点。

简单来说，如果顶点 $v{i_0}$ 可以通过一系列的顶点和边，到达顶点 $v{i_m}$，则称顶点 $v{i_0}$ 和顶点 $v{i_m}$ 之间有一条路径，其中经过的顶点序列则称为两个顶点之间的路径。

• 环（Circle）：如果一条路径的起始点和终止点相同（即 $v{i_0} = v{i_m}$ ），则称这条路径为「回路」或者「环」。

• 简单路径：顶点序列中顶点不重复出现的路径称为「简单路径」。

而根据图中是否有环，我们可以将图分为「环形图」和「无环图」。

• 环形图（Circular Graph）：如果图中存在至少一条环路，则该图称为「环形图」。

• 无环图（Acyclic Graph）：如果图中不存在环路，则该图称为「无环图」。

特别的，在有向图中，如果不存在环路，则将该图称为「有向无环图（Directed Acyclic Graph）」，缩写为 DAG。因为有向无环图拥有为独特的拓扑结构，经常被用于处理动态规划、导航中寻求最短路径、数据压缩等多种算法场景。

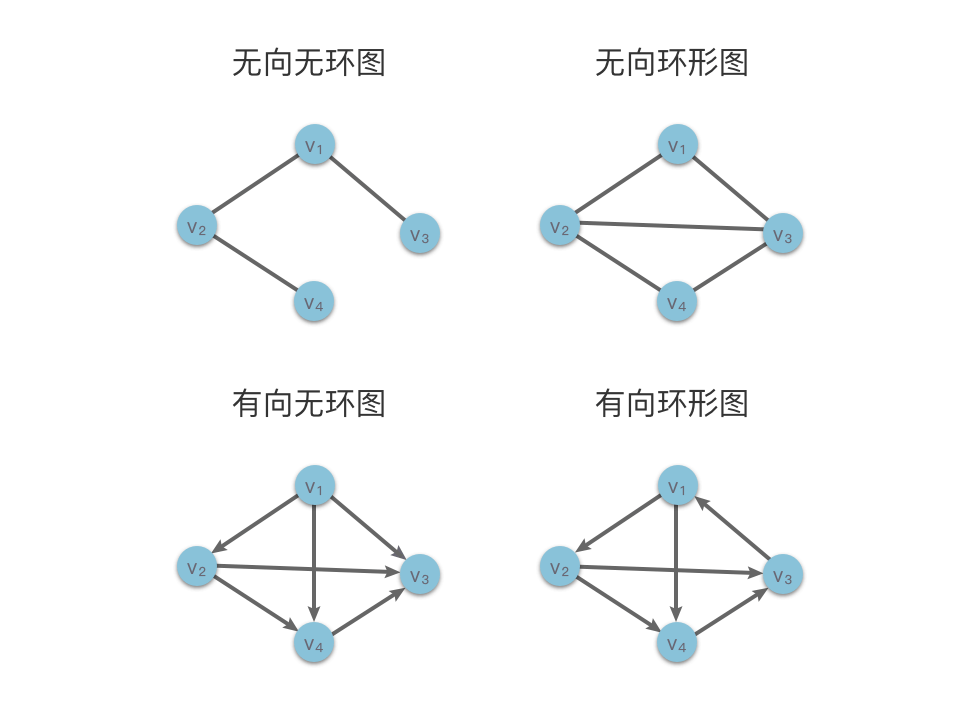
如下图所示，分别为：无向无环图、无向环形图、有向无环图和有向环形图。其中有向环形图中的顶点 $v_1$、$v_2$、$v_3$ 与相连的边构成了一个环。

2.3 连通图和非连通图

2.3.1 连通无向图和连通分量

在无向图中，如果从顶点 $v_i$ 到顶点 $v_j$ 有路径，则称顶点 $v_i$ 和 $v_j$ 是连通的。

• 连通无向图：在无向图中，如果图中任意两个顶点之间都是连通的，则称该图为连通无向图。

• 非连通无向图：在无向图中，如果图中至少存在一对顶点之间不存在任何路径，则该图称为非连通无向图。

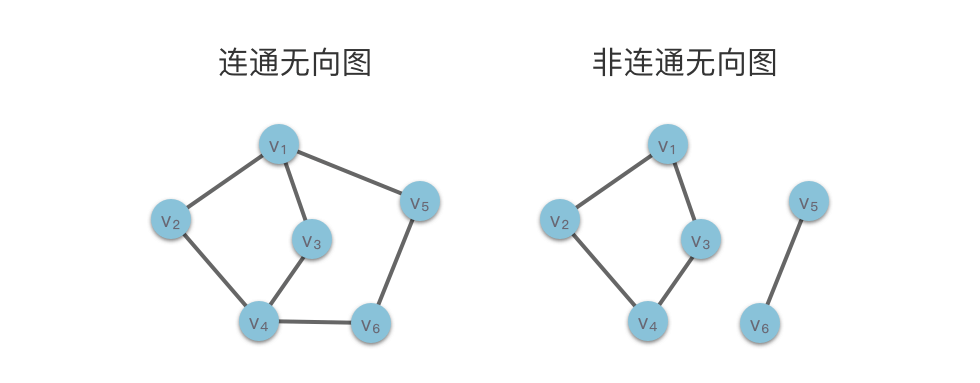
如下图所示，左侧图中 $v_1$ 与 $v_2$、$v_3$、$v_4$、$v_5$、$v_6$ 都是连通的，所以该图为连通无向图。右侧图中 $v_1$ 与 $v_2$、$v_3$、$v_4$ 都是连通的，但是 $v_1$ 和 $v_5$、$v_6$ 之间不存在任何路径，则该图为非连通无向图。

下面介绍一下无向图的「连通分量」概念。有些无向图可能不是连通无向图，但是其子图可能是连通的。这些子图称为原图的连通子图。而无向图的一个极大连通子图（不存在包含它的更大的连通子图）则称为该图的「连通分量」。

• 连通子图：如果无向图的子图是连通无向图，则该子图称为原图的连通子图。

• 连通分量：无向图中的一个极大连通子图（不存在包含它的更大的连通子图）称为该图的连通分量。

• 极⼤连通⼦图：无向图中的一个连通子图，并且不存在包含它的更大的连通子图。

例如上图中右侧的非连通无向图，其本身是非连通的。但顶点 $v_1$、$v_2$、$v_3$、$v_4$ 与其相连的边构成的子图是连通的，并且不存在包含它的更大的连通子图了，所以该子图是原图的一个连通分量。同理，顶点 $v_5$、$v_6$ 与其相连的边构成的子图也是原图的一个连通分量。

2.3.2 强连通有向图和强连通分量

在有向图中，如果从顶点 $v_i$ 到 $v_j$ 有路径，并且从顶点 $v_j$ 到 $v_i$ 也有路径，则称顶点 $v_i$ 与 $v_j$ 是连通的。

• 强连通有向图：如果图中任意两个顶点 $v_i$ 和 $v_j$，从 $v_i$ 到 $v_j$ 和从 $v_j$ 到 $v_i$ 都有路径，则称该图为强连通有向图。

• 非强连通有向图：如果图中至少存在一对顶点之间不存在任何路径，则该图称为非强连通有向图。

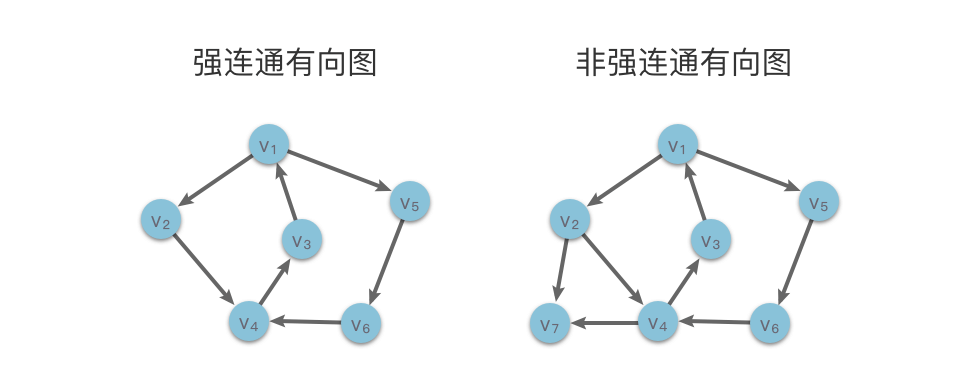
如下图所示，左侧图中任意两个顶点之间都有路径，则左侧图为强连通有向图。右侧图中顶点 $v_7$ 无法通过路径到达其他顶点，则右侧图为非强连通有向图。

与无向图类似，有向图的一个极大强连通子图称为该图的 强连通分量。

• 强连通子图：如果有向图的子图是连通有向图，则该子图称为原图的强连通子图。

• 强连通分量：有向图中的一个极⼤强连通⼦图，称为该图的强连通分量。

• 极⼤强连通⼦图：有向图中的一个强连通子图，并且不存在包含它的更大的强连通子图。

例如上图中，右侧的非强连通有向图，其本身不是强连通的（顶点 $v_7$ 无法通过路径到达其他顶点）。但顶点 $v_1$、$v_2$、$v_3$、$v_4$、$v_5$、$v_6$ 与其相连的边构成的子图（即上图的左侧图）是强连通的，并且不存在包含它的更大的强连通子图了，所以该子图是原图的一个强连通分量（即上图中的左侧图是右侧图的强连通分量）。同理，顶点 $v_7$ 构成的子图也是原图的一个强连通分量。

2.4 带权图

有时，图不仅需要表示顶点之间是否存在某种关系，还需要表示这一关系的具体细节。这时候我们需要在边上带一些数据信息，这些数据信息被称为 权。在具体应用中，权值可以具有某种具体意义，比如权值可以代表距离、时间以及价格等不同属性。

• 带权图：如果图的每条边都被赋以⼀个权值，这种图称为带权图。

• 网络：带权的连通⽆向图称为⽹络。

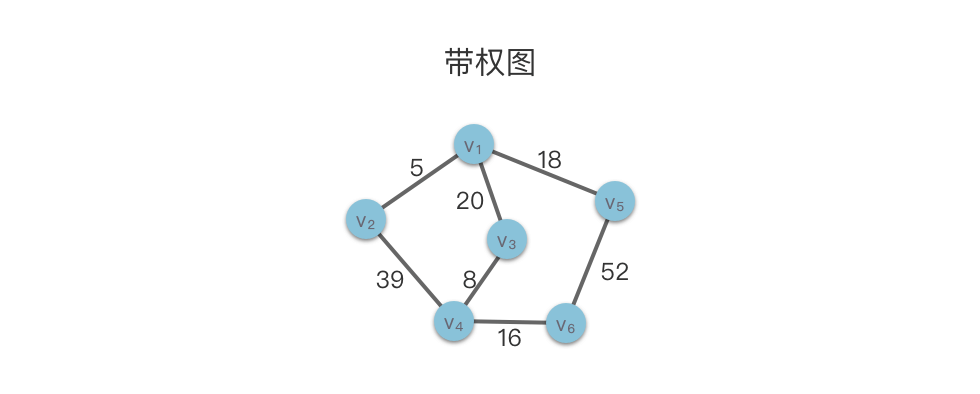
在下面的示意图中，我们给出了一个带权图的例子。

2.5 稠密图和稀疏图

根据图中边的稀疏程度，我们可以将图分为「稠密图」和「稀疏图」。这是一个模糊的概念，目前为止还没有给出一个量化的定义。

• 稠密图（Dense Graph）：有很多条边或弧（边的条数 e 接近于完全图的边数）的图称为稠密图。

• 稀疏图（Sparse Graph）：有很少条边或弧（边的条数 e 远小于完全图的边数，如 $e < nlog_2n$）的图称为稀疏图。