- 1DataWhale打卡Day01--推荐系统入门_隐语义模型与矩阵分解 协同过滤算法的特点: 协同过滤算法的特点就是完全没有利用
- 2知识图谱——事件抽取
- 3Golang 学习笔记3:Go 并发与网络_go 接口并发
- 4从GitHub克隆项目到本地
- 5卷完了!分享下我的秋招面经(投递近50家自动驾驶与机器人公司)_杉川机器人结构创新工程师面试经验
- 62020B证(安全员)模拟考试系统及B证(安全员)考试试题_安全员b证历年真题试卷网盘
- 7Transformer的位置编码笔记(positional encoding)_transformer位置编码为啥用sin和cos
- 8git从tag拉分支_git 从tag拉分支
- 9IDEA JRebel最新版(2024.2.0)在线激活以及配置_idea插件jrebel 2024.2.0激活
- 10谷歌将正式推出 Fuchsia OS,已有适配设备_fuchsia os支持设备
明翰数据结构与算法笔记V0.8(持续更新)_弗明翰算法
赞
踩
前言
数据结构 + 算法 = 程序。
无论从事前端还是后端,无论使用什么编程语言,
只要想进大厂,都绕不开考核数据结构与算法这道坎,
本文中的代码均用Java编写,当然,也可以使用其他语言来实现。
其实编程语言并不是最重要的,思想才是,逻辑思维才是。
本文大部分内容并不是作者原创,
只是记录作者在学习算法与数据结构过程中的点点滴滴,
如有侵权,请在评论中及时指出。
本文理论上是对[新手/小白]友好的,
如果有不明白的地方可以评论指出。
本文内容较多,
建议先纵览一下文章顶部的目录,
再结合左侧目录阅读。
先把基本的数据结构弄明白,例如:数组,链表,哈希表等等。
之后再去看一些基本的算法,例如:枚举,递归,二分查找等等。
再循序渐进。
注意事项:
[堆栈]作为计算机科学中的一个专有词语,操作系统中的[堆栈]和数据结构中的[堆栈]不是一个概念;- 算法中的[枚举]与Java中的[枚举]不是一个概念;
基本概念:
- [遍历/迭代]:迭代通常指在数据结构中按顺序逐个访问元素的过程,例如使用循环语句逐个访问数组、列表或树中的元素。遍历通常指访问整个数据结构中的所有元素,无论是按照某种特定的顺序还是按照某种规则,例如深度优先搜索算法和广度优先搜索算法都是树的遍历算法;
数据结构
数据结构可以优化算法效率,同一个算法用不同的数据结构,
可能会带来完全不一样的时间和空间(时间与空间互换)。
例如:平衡二叉树与数组都能实现查找功能,
但两者的时间复杂度分别是:O(n),O(logn)。
涉及到时间复杂度的地方,如果读者不懂,
可以先跃迁至本文的“算法”部分,里面有个小章节有专门讲解。
不管是什么数据结构,在内存中的存储中方只有两种:
数组(顺序存储);链表(链式存储);
[常用/常见]数据结构:
数组;链表;- [散列表/哈希表];
- 栈与队列;
二叉树;- 堆;
- 跳表;
- 图;
- [Trie树/字典树];
- 字符串;
以下是最简单的十个数据结构,按照难易程度排序:
- 数组:一组连续的内存单元,可以存储相同类型的数据。
- 链表:一组通过指针连接在一起的节点,每个节点包含数据和指向下一个节点的指针。
- 栈:一种后进先出(LIFO)的数据结构,可以在栈顶进行插入和删除操作。
- 队列:一种先进先出(FIFO)的数据结构,可以在队尾插入和在队头删除元素。
- 树:一组通过边连接在一起的节点,每个节点可以有多个子节点。
- 图:一组通过边连接在一起的节点,每个节点可以有多个相邻节点。
- 哈希表:通过哈希函数将键映射到值的数据结构。
- 堆:一种可以快速找到最大或最小值的数据结构,可以用数组或树实现。
- 并查集:一种用于维护集合的数据结构,可以高效地判断两个元素是否在同一集合中。
- 字典树:一种用于高效地存储和搜索字符串的数据结构,可以支持前缀搜索和字符串匹配。
线性表
线性表是最容易理解的数据结构,这是一切开始的地方,
线性表是指存储了多个数据元素的数据结构,
其中的元素是按照线性顺序排列的,
元素具有相邻关系,每个元素最多只有一个前驱和一个后继,
可以按照一定顺序进行存储和访问。
常见的线性表有:数组、链表、队列和栈等。
- 数组适用于随机访问元素的场景;
- 链表适用于插入和删除元素频繁的场景;
- 栈适用于表达式求值和括号匹配等场景;
- 队列适用于消息传递和任务调度等场景;
- 双向链表适用于需要双向遍历的场景;
- 循环链表适用于需要遍历整个列表的场景;
数组
数组在内存中是紧凑连续的存储,可以随机访问,
通过[索引/index]可以快速找到对应元素,
而且相对节约存储空间。
但正因为连续存储,所以内存空间必须一次性分配够,
如果数组要扩容,则需要重新分配一块更大的空间,
再把数据全部复制过去,时间复杂度为 O(N)。
如果想在数组中间进行插入和删除,
每次必须移动后面的所有数据以保持连续,时间复杂度为 O(N)。
这是一个简单的数组的使用示例,
通过定义数组,赋值,遍历等方式来说明数组的使用方法:
public class ArrayExample { public static void main(String[] args) { // 定义数组并初始化 int[] numbers = new int[]{1, 2, 3, 4, 5}; // 输出数组内容 for (int i = 0; i < numbers.length; i++) { System.out.println(numbers[i]); } // 修改数组内容 numbers[2] = 6; // 再次输出数组内容 for (int i = 0; i < numbers.length; i++) { System.out.println(numbers[i]); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
树状数组:
树状数组是一种数组。它是一种用于处理序列上的信息的数据结构,
由于其维护的信息的树形结构,因此得名为树状数组。
树状数组用于解决问题,例如查询区间和,单点修改等。
它可以通过使用树形结构加速查询和修改操作,从而提高处理效率。
树状数组的算法复杂度通常是 O(log n),
因此在很多场景下可以高效地处理数据。
链表
链表是一种通过链式关系存储数据元素的线性表,
其中每个元素都是一个节点,
每个节点都存储了该元素的数据和一个指向下一个元素的指针。
链表是线性表的一种重要的实现方式,
它比数组等其他存储结构具有更好的灵活性和可扩展性。
链表因为元素不连续,而是靠指针指向下一个元素的位置,
所以不存在数组的扩容问题。
如果知道某一元素的前驱和后驱,
操作指针即可删除该元素或者插入新元素,时间复杂度 O(1)。
但是正因为存储空间不连续,
你无法根据一个[索引/index]算出对应元素的地址,所以不能随机访问。
而且由于每个元素必须存储指向前后元素位置的指针,
会消耗相对更多的储存空间。
// 定义链表节点类 class ListNode { int val; ListNode next; public ListNode(int val) { this.val = val; } } public class LinkedListExample { public static void main(String[] args) { // 初始化链表 ListNode head = new ListNode(1); head.next = new ListNode(2); head.next.next = new ListNode(3); // 遍历链表 ListNode current = head; while (current != null) { System.out.println(current.val); current = current.next; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
其中,ListNode 类定义了链表的节点,val 表示该节点的值,
next 表示该节点的下一个节点。
在主函数中,通过连接多个节点初始化链表,
并通过循环遍历输出链表中的值。
单向链表:
双向链表:
在链表的基础上,每个节点还包含一个指向前一个节点的指针。
循环链表:
在链表的基础上,最后一个节点指向第一个节点,形成一个环。
循环链表是一种特殊的链表,
其中最后一个元素的指针指向第一个元素,
从而形成一个环。
循环链表可以在遍历链表元素时使用,
并且可以在没有特殊情况的情况下无限循环。
跳表:
跳表是一种有序的数据结构,它通过在数据间增加跳转指针来提高查询效率。
跳表中的每个节点都包含一个键值和一些指向其他节点的指针。
这些指针分别指向当前节点在更高层次中的下一个节点。
通过使用跳转指针,可以减少搜索的节点数,从而加快查询速度。
跳表是一种优化的链表数据结构,其时间复杂度为O(logN),
非常适合在数据量较大的情况下对有序数据进行查询、插入和删除操作。
栈与队列
栈,Stack,又名堆栈,是[后进先出/先进后出]的线性表数据结构,
其只有一端(栈顶)可以任意进出元素,
而另一端(栈底)则无法进行任何操作。
它是一种运算受限的线性表。
其限制是仅允许在表的一端进行插入和删除运算。
这一端被称为栈顶,相对地,把另一端称为栈底。
向一个栈插入新元素又称作[进栈/入栈/压栈],
它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素。
从一个栈删除元素又称作[出栈/退栈],它是把栈顶元素删除掉,
使其相邻的元素成为新的栈顶元素。
其运行方式如下:
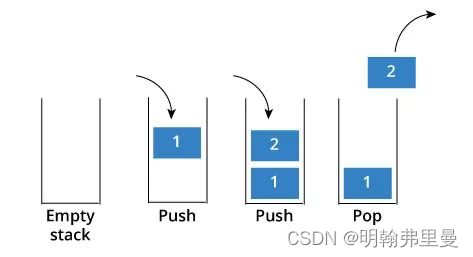

使用[栈]主要记住的方法:
push(),压入;pop(),弹出;- peek(),栈顶;
- size(),长度;
import java.util.Stack; public class StackExample { public static void main(String[] args) { // 创建一个空栈 Stack<Integer> stack = new Stack<>(); // 向栈顶加入元素 stack.push(1); stack.push(2); stack.push(3); // 栈内元素数量 System.out.println(stack.size()); // 打印栈内元素 System.out.println("栈内元素:" + stack); // 输出:栈内元素:[1, 2, 3] while(!stack.isEmpty()){ // 访问栈顶元素 System.out.println("栈顶元素1:" + stack.peek()); // 输出:栈顶元素:3 // 访问并删除栈顶元素 System.out.println("栈顶元素2:" + stack.pop()); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
栈的使用场景:
- 反转数组元素,把最后一个元素放到第一个下标;
- 函数调用:函数调用栈通常用于存储函数的调用和返回地址。每次调用函数时,都将当前函数的返回地址压入栈中,以便在函数返回时能够返回正确的位置;
- 迷宫求解:在深度优先搜索算法中,通常使用栈来存储当前搜索路径。当搜索到死路时,可以将栈顶元素弹出并返回到前一个节点以继续搜索,别急,后面会学到;
- 撤销操作:在许多应用程序中,如文本编辑器、图像编辑器等,栈用于存储用户的撤销操作。每次用户执行一个操作时,该操作的状态都将推入栈中,以便在需要撤销时可以恢复到之前的状态;
队列是[先进先出]的线性表数据结构,其中元素只能从队尾进,从队首出。
如下图所示,元素依次入队又依次出队。
另外,有标记的位置分别代表队首与队尾,其中左边为队首。
队列是一种特殊的线性表,
特殊之处在于它只允许在表的前端(front)进行删除操作,
而在表的后端(rear)进行插入操作,和栈一样,
队列是一种操作受限制的线性表。
进行插入操作的端称为队尾,进行删除操作的端称为队头。
队列中没有元素时,称为空队列。

使用[队列]主要记住的方法:
offer(),在队列尾部添加一个元素,但不会抛出异常,而是返回false(如果队列已满)或true(如果添加成功);add(),在队列尾部添加一个元素,如果队列已满,则抛出IllegalStateException异常;poll(),从队列的头部删除并返回第一个元素。如果队列为空,则返回null;remove(),从队列的头部删除并返回第一个元素。如果队列为空,则抛出NoSuchElementException异常;- size(),长度;
import java.util.LinkedList; import java.util.Queue; public class QueueExample { public static void main(String[] args) { // 创建队列 Queue<Integer> queue = new LinkedList<>(); // 向队列中加入数据 queue.offer(1); queue.offer(2); queue.offer(3); // 从队列头部取出数据 System.out.println(queue.poll()); // 输出:1 // 检查队列是否为空 System.out.println(queue.isEmpty()); // 输出:false // 检查队列大小 System.out.println(queue.size()); // 输出:2 // 从队列头部取出数据,若队列为空,则返回null System.out.println(queue.peek()); // 输出:2 // 清空队列 queue.clear(); // 检查队列是否为空 System.out.println(queue.isEmpty()); // 输出:true } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
双端队列:具有队列和栈双重性质的线性表数据结构。
单调栈:
在基础栈上稍加改动所形成的[单调栈]算法,
该算法与[单调队列]组成了算法题中最常考察的线性数据结构。
顾名思义,[单调栈]就是栈内元素满足单调性的栈结构。
此处的单调性分为[单调递增]与[单调递减],
为了便于描述,接下来以[单调递增栈]为例进行讲解。
[单调递增栈]就是栈内元素满足单调递增,
假设当前元素为x,若栈顶元素≤x,则将x入栈,
否则不断弹出栈顶元素,直至栈顶元素≤x。
我们仍以3,1,4,5,2,7为例,其[单调递增栈]具体过程如下图所示。
不难发现,入栈结束后,栈中仅保留了1,2,7,
其中3由于比1大被弹出,而4,5则由于比2大被弹出。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WWEWe4Qe-1684831719293)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4012)]
在栈中维护单调性究竟有什么用呢?
要回答这个问题,
我们首先来观察一下上述示例中2为当前元素时的状态,如下图所示。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ySImYhpY-1684831719293)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4013)]
在该状态中,栈顶元素为5,而当前元素为2,由于5比2大,
即此时若将2放入栈内,则不满足单调递增,因此需要将5弹出栈。
这时请大家思考,2和5之间是否有什么更深层的关系,
所以才导致了5最终被2弹出?
仔细观察原始序列3,1,4,5,2,7,
我们可以发现2是5右边第一个比它小的数。
基于这个发现,我们再次回顾「栈顶元素被弹出,当且仅当栈顶元素 > 当前元素」这一条件,
因此我们可以得知对于单调递增栈,若栈顶元素被弹出,
则当前元素为其右边第一个比它小的数。
2弹出5后,栈顶变为4,此时4仍比2大,
因此4也被弹出,这时可确定2是4右边第一个比它小的数。
4被弹出后,栈顶变为1,1≤2,因此2被放入栈,此时栈内状态如下图所示。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VhIFzm4P-1684831719298)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4014)]
按照刚才的思路,我们继续思考为何最终状态下2的左边是1,
这两个数之间又有何关联?
继续观察原始序列3,1,4,5,2,7,
可以发现1是2左边第一个小于等于它的数,稍加思考后,
我们可以得知当一个数字被放入单调递增栈时,
其栈内左边的数是它在原始序列中,左边第一个小于等于它的数。
至此我们可以解答最开始的疑问,
单调栈的根本作用在于求得每一个数字在原始序列中[左/右]边第一个[大于/小于]它自身的数字,
并且由于每一个数字只会入栈一次且最多出栈一次,
因此总的时间复杂度为 O(n)。
另外需要注意,一次「单调递增栈」的过程,
可以求得每个数字左边第一个小于等于它的数,
以及右边第一个小于它的数,此处需注意「小于等于」和「小于」的区别。
除此之外,「单调递减栈」将上述的「小于」改为「大于」即可成立。
单调队列:
[单调队列]在[数据结构]题中的分布较为广泛,
且常被当作优化[动态规划]的一种重要手段。
顾名思义,[单调队列]就是队列内元素满足单调性的队列结构。
且为了满足队列内元素的单调性,队尾也可弹出元素。
此处的单调性分为单调递增与单调递减,
为了便于描述,接下来以[单调递增队列]为例进行讲解。
[单调递增队列]中[队尾]的操作与[单调递增栈]中[栈顶]的操作一致,
即假设当前元素为x,若队尾元素<=x,则将x入队,
否则不断弹出队尾元素,直至队尾元素<=x。
例如以3,1,4,5,2,7,为例,
若[队首]始终不弹出元素,则其具体过程如下图所示。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QDJVXdv9-1684831719299)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4015)]
由此可知,[单调队列]与[单调栈]的最大区别就在于[队首]的操作,
何时将队首元素出队是[单调队列]算法的关键。
然而[队首]的操作往往具有多样性,并非一成不变。
[串/字符串]
串是一种特殊的字符序列,它是通过一系列字符组成的,
每个字符具有[前驱/后继]关系。因此,串可以看作是字符线性表,
其中的字符元素按照其在串中的顺序确定。
在计算机科学中,串是一个重要的数据结构,
广泛用于文本处理、字符串匹配等问题的解决方案。
记住一些常用方法:
显示字符串长度是length();获取字符串中的某一个字符用charAt(),如果字符串为"",调用该方法会抛异常;
public class StringExample { public static void main(String[] args) { // 创建字符串 String str1 = "Hello"; String str2 = new String("World"); char[] array = new char[]{'a', 'b', 'c', 'd', 'e'}; String str3 = new String(array, 0, 3); // 获得字符串中下标为0的字符 char c = str1.charAt(0); // 拼接字符串 String str3 = str1 + " " + str2; System.out.println(str3); // Hello World // 获取字符串长度 int length = str3.length(); System.out.println("字符串长度:" + length); // 11 // 判断字符串是否相等 boolean equals = str1.equals(str2); System.out.println("字符串是否相等:" + equals); // false // 查找子字符串 int index = str3.indexOf("World"); System.out.println("子字符串索引:" + index); // 6 // 截取字符串 String subString = str3.substring(6); System.out.println("截取后的字符串:" + subString); // World String str = "abcdefg"; System.out.println("---获得字符串任意下标的字符---"); System.out.println(str.charAt(0)); System.out.println(str.charAt(1)); System.out.println(str.charAt(2)); System.out.println("---字符串转换成char数组---"); char[] chars = str.toCharArray(); for(int i = 0; i < chars.length; i++){ System.out.println(chars[i]); } System.out.println("---小驼峰转蛇形---"); String s = "orderOptionId"; String zz = s.replaceAll("[A-Z]", "_$0").toLowerCase(); System.out.println(zz); System.out.println("---获取字符下标---"); String x = "ababc"; System.out.println(x.lastIndexOf("ab")); System.out.println(x.indexOf("ab")); String aa = "aaaalimitbbbb"; System.out.println(aa.indexOf("limit"));//4 System.out.println(aa.substring(aa.indexOf("limit")+5, aa.length()));//bbbb System.out.println(aa.substring(aa.indexOf("limit")+5));//bbbb System.out.println(aa.substring(0,aa.indexOf("limit")+5));//aaaalimit System.out.println(aa.substring(aa.indexOf("l")));//limitbbbb System.out.println(aa.substring(aa.indexOf("limit")));//limitbbbb String aaa = "SELECT gender,key_id,user_name,phone FROM t_user ".toLowerCase(); System.out.println(aaa.substring(aaa.indexOf("select")+6, aaa.indexOf("from")).trim()); //gender,key_id,user_name,phone } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
字典树:
未完待续
后缀树:
未完待续
树
树是一种非线性数据结构,由n个节点组成,其中一个节点称为根节点,
剩余节点分为m个互不相交的子树。
每个子树又是一棵树,
即每个子树都可以看作是一个节点和它的所有子节点组成的树。
树的节点包含一个数据元素以及指向其子节点的指针或引用。
每个节点可以有任意数量的子节点,
但每个节点只有一个父节点,除了根节点没有父节点,叶节点没有子节点。
树的常见应用包括文件系统、数据库索引、HTML文档、编译器语法树等。
常见的树结构包括二叉树、平衡树、B树、红黑树等。
树的遍历方式(如果有子树,则先走子树,再走自己):
- 前序遍历,按照“根左右”的顺序遍历一棵树,通常使用递归或栈来实现;
- 中序遍历,按照“左根右”的顺序遍历一棵树,适用于二叉树,中序遍历是树遍历中的一种重要方式,由于它的遍历顺序与二叉搜索树的排序顺序一致,因此在二叉搜索树中,中序遍历可以按照从小到大的顺序输出所有节点值;
- 后序遍历,按照“左右根”的顺序遍历一棵树,后序遍历在解决一些树相关问题时很有用,例如计算二叉树的深度和直径等;
- 层次遍历;
一些概念:
- 节点的度:一个节点含有的子节点的个数称为该节点的度;
- 树的度:一棵树中,最大的节点的度称为树的度;
叶子节点:度为0的节点;- 树的阶:树中最大子节点数量,二叉树的阶是2,三叉树的阶是3;
// 树节点类 class TreeNode { int val; TreeNode left; TreeNode right; public TreeNode(int val) { this.val = val; } } public class TreeExample { public static void main(String[] args) { // 创建根节点 TreeNode root = new TreeNode(1); // 左子树 root.left = new TreeNode(2); root.left.left = new TreeNode(4); root.left.right = new TreeNode(5); // 右子树 root.right = new TreeNode(3); root.right.right = new TreeNode(6); // 遍历树 preOrder(root); } // 先序遍历 public static void preOrder(TreeNode node) { if (node == null) { return; } System.out.print(node.val + " "); preOrder(node.left); preOrder(node.right); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
最近公共祖先:
在树形数据结构中,最近公共祖先(Lowest Common Ancestor, LCA)是指两个节点在树形结构中的公共祖先中,
距离两个节点最近的节点。
最近公共祖先在很多情况下都是需要求解的问题,
例如:在计算机科学中求两个文件的公共祖先;
在生物学中求两个物种的公共祖先;在图论中求两个节点的公共祖先。
在求解最近公共祖先的问题时,通常使用多种算法,
例如:暴力递归算法,倍增算法,树剖算法等。
每种算法的时间复杂度和空间复杂度都有所不同,
因此在实际应用中应根据需求选择适当的算法。
并查集
并查集是一种树型的数据结构,
常用于处理一些不相交集(Disjoint Sets)问题。
它用于维护一组不相交的集合,每个集合用一个树来表示。
在并查集中,每个元素最开始都是一个单独的集合。
并查集提供两个主要的操作:
查询两个元素是否在同一个集合中,以及合并两个元素所在的集合。
并查集的优点在于,它可以高效地处理动态集合问题,
并且可以在线性时间内查询两个元素是否在同一个集合中。
并查集通常用于以下应用场景:联通块问题,动态图的生成树等。
它的算法复杂度为 O(α(n)),
其中 α(n) 是一个极慢增长的逆反 Ackermann 函数,
因此并查集的时间复杂度在实际情况中近似于常数。
二叉树
前中后序遍历
[二叉排序树/二叉搜索树]
二叉排序树和二叉搜索树是同一个概念,指一种特殊的二叉树,
对于树中的任意一个节点,左子树中的所有节点的值都小于该节点的值,
右子树中的所有节点的值都大于该节点的值。
[二叉排序树/二叉搜索树]是一种非常有效的数据结构,
这种特殊的结构容易进行查询、插入和删除操作,
可以广泛用于实现字典和搜索引擎等应用。
二叉排序树的一个重要应用是在查找和排序算法中。
由于其有序性质,二叉排序树可以快速地查找一个元素,
时间复杂度为O(log n)。
二叉搜索树的左子树永远是比根节点小,
而它的右子树则永远比根节点大。
8
/ \
3 10
/ \ \
1 6 14
/ \ /
4 7 13
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
比较适合找树中的[最大值节点/最小值节点],
最小值在树的最最最左侧,最大值在树的最最最右侧。
红黑树
红黑树,Black Red Tree,是一种自平衡的[二叉排序树/二叉搜索树]。
它具有[二叉排序树/二叉搜索树]的性质,
即:每个节点的左子树都小于它,右子树都大于它。
普通的[二叉排序树/二叉搜索树]在极端的情况下可退化成链表,
此时的查找效率会比较低下。
为了避免这种情况,就出现了一些自平衡的[二叉排序树/二叉搜索树],
比如AVL、红黑树等。
但是,红黑树除了二叉搜索树的性质外,还具有特殊的颜色规则,
这使得它在保证平衡的同时还能保证。。。
它们通过定义一些性质,将任意结点的左右子树高度差控制在固定范围内,
以达到平衡状态。红黑树需要满足如下五条性质:
- 节点只能是红色或者黑色;
- 根节点永远是黑色;
- 每个[空/NULL]的叶子节点是黑色;
- 每个红色节点的两个子节点必须都是黑色,父节点与子节点不能是连续的红色;
- 从任一节点到其每个最末端的叶子的所有简单路径都包含相同数目的黑色节点(简称黑高),从根节点到每一个NULL节点的路径中,都包含了相同数量的黑色节点;
这五条性质约束了红黑树,可以通过数学来证明,
满足这五条性质的二叉树,
就可以保证任意节点到其每个叶子节点路径最长不会超过最短路径的2倍。
证明如下:
当某条路径最短时,这条路径比如都是黑色节点构成。
当某条路径长度最长时,这条路径必然是由红色和黑色节点相间构成。
而又限定了从任一节点到其每个叶子节点的所有路径必须包含相同数量的黑色节点。
此时,在路径最长的情况下,路径上红色节点数量 = 黑色节点数量。
该路径长度为黑色节点数量的2倍,也就是最短路径长度的2倍。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oMtTxOCS-1684831719302)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4019)]
其特殊的颜色规则和大小关系保证了树的高度最多为O(log n),
从而保证了查询、插入和删除操作的最坏复杂度为O(log n)。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gSVvymgQ-1684831719305)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4018)]
因此,红黑树是一种特殊的二叉树,具有二叉树的一些性质,
但也具有自己独特的性质,并且广泛应用于许多算法中,
例如在操作系统内存管理、数据库索引等方面。
红黑树操作
红黑树的基本操作与其他树的操作一样,有查找、插入和删除等操作。
由于查找与其他树的操作一样,比较简单,而插入、删除操作比较复杂,
这里主要就是接受插入、删除操作。
旋转操作:
由于插入、删除的过程中都要涉及到旋转,
这里首先介绍一下旋转这个基本操作,旋转操作分为左旋转和右旋转。
左旋转的过程如下:
- 对于根节点A,如果它的右子树较高,那么我们需要对它进行左旋转;
- 将根节点A向左移动,同时将根节点的右子节点B变为新的根节点;
- 新的根节点B的左子树变为原根节点A的右子树;
- 原根节点A的右子树变为新的根节点B的右子树;
A B
/ \ / \
T1 B --->(left rotate) A T3
/ \ / \
T2 T3 T1 T2
- 1
- 2
- 3
- 4
- 5
右旋转的过程如下:
- 对于根节点A,如果它的左子树较高,那么我们需要对它进行右旋转;
- 将根节点A向右移动,同时将根节点的左子节点B变为新的根节点;
- 新的根节点B的右子树变为原根节点A的左子树;
- 原根节点A的左子树变为新的根节点B的左子树;
A B
/ \ / \
B T3 --->(right rotate) T1 A
/ \ / \
T1 T2 T2 T3
- 1
- 2
- 3
- 4
- 5
插入操作:
红黑树的插入过程和[二叉排序树/二叉搜索树]的插入过程基本类似,
不同的地方在于,红黑树插入新节点后,需要进行调整,
以满足红黑树的性质。
在讨论红黑树的插入操作之前必须要明白,
任何一个即将插入的新节点的初始颜色都为红色。
原因很简单,引入插入黑色的节点会增加某条路径上黑节点的数目,
从而导致整棵树黑高度的不平衡。
但如果插入的节点是红色的,此时所有路径上的黑色节点数量不变,
仅可能会出现两个连续的红色节点的情况。
这种情况下,通过变色和旋转进行调整即可,比插入黑色的简单多了。
红黑树的插入可能遇到如下几种情况:
- 情况1,当插入的节点是根节点时,直接涂黑即可;
- 情况2,当要插入的节点的父节点是黑色的时候,这个时候插入一个红色的节点并没有对这五个性质产生破坏。所以直接插入不用在进行调整操作;
- 情况3,如果要插入的节点的父节点是红色且叔叔节点也是红色。由于父节点和插入的节点都是红色,所以性质4被打破,此时需要进行调整。在这种情况下,先将父节点和叔叔节点的颜色染成黑色,再让祖父结点染成红色。此时经过祖父结点的路径上的黑色节点数量不变,性质5仍然满足。但需要注意的是祖父节点被染成红色后,可能会和它的父节点形成连续的红色节点,此时需要递归向上调整;
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y7t2gL28-1684831719305)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENNote/p551?hash=7172c446bc3fc4091c5ce65fd70be129)] - 情况4,当要插入的父节点为红色,叔叔节点为黑色。此时需要对父节点进行左旋,然后按照情况5进行处理(注:这里要插入的节点有可能是调整后的其它节点,这里我们理解父节点为插入节点而转到情况5,
感觉这里有问题,刚开始的叔叔节点不是黑色);
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sbHWvTdS-1684831719308)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4024)] - 情况5,当要插入的父节点为红色,叔叔节点为黑色。插入节点是父节点的左孩子,且父节点是祖父节点的左孩子。此时对祖父节点进行右旋,并将祖父节点和父节点进行互换颜色。这时候满足了红黑树的全部性质;
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ncTqtNbO-1684831719310)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4025)]
删除操作:
相对于插入操作,红黑树的删除操作更为复杂。
同样,这里我们也分为几种情况进行分析:
- 情况1,当被删除元素为红时,对五条性质都没有什么影响,直接删除即可;
- 情况2,当被删除元素为黑且为根节点时,直接删除;
- 情况3,当被删除元素为黑,且有一个右子节点为红时,将右子节点涂黑放到被删除元素的位置,如图:[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TRzvhdCX-1684831719311)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4026)]
- 情况4,当被删除元素为黑,且兄弟节点为黑,兄弟节点两个孩子也为黑,父节点为红,此时,交换兄弟节点与父节点的颜色;NULL元素是指每个叶节点都是两个空的元素,颜色为黑的NULL元素,需要他的时候就可以把它看成两个黑元素,不需要的时候就可以忽视它;[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-uqOKUvtc-1684831719311)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4027)]
- 情况5,当被删除的元素为黑、并且为父节点的左支,且兄弟颜色为黑,兄弟的右支为红色,这个时候需要交换兄弟与父亲的颜色,并把富且涂黑、兄弟的右支涂黑,并以父节点为中心左转;[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2YgqAUYr-1684831719312)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4028)]
- 情况6,当被删除元素为黑、并且为父节点的左支,且兄弟颜色为黑,兄弟的左支为红色,这个时候需要先把兄弟与兄弟的左子节点颜色互换,进行右转,然后就变成了情况5一样,在按照情况5进行旋转;[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SCMK3WOj-1684831719313)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4029)]
- 情况7,当被删除元素为黑且为父元素的右支时,跟情况5、情况6互为镜像;
- 情况8,当被删除的元素为黑,且父父元素的左支,兄弟节点为红色的时候,需要交换兄弟节点与父节点的颜色,以父节点进行左旋,就变成了情况4,再按照情况四进行操作即可;[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9g8nXiUb-1684831719315)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4030)]
霍夫曼树
未完待续
堆
堆是一种特殊的二叉树数据结构。
它是一种完全二叉树,具有以下特殊性质:
- 堆中的每个节点都必须满足一定的性质,这取决于它是最大堆还是最小堆,对于最大堆,父节点的值总是大于等于它的子节点。对于最小堆,父节点的值总是小于等于它的子节点;
因此,堆是一种特殊的二叉树,具有二叉树的一些性质,
但也具有自己独特的性质。
堆的应用非常广泛,例如堆排序,最小生成树等。
堆常用于构建优先队列等问题的解决方案。
堆(heap)也被称为优先队列,
队列中允许的操作是 先进先出(FIFO),
在队尾插入元素,在队头取出元素。
而堆也是一样,在堆底插入元素,在堆顶取出元素。
二叉树的衍生,有最小堆最大堆的两个概念,
将根节点最大的堆叫做[最大堆/大根堆],
根节点最小的堆叫做[最小堆/小根堆]。
常见的堆有二叉堆、斐波那契堆等。
[大/小]根堆
可并堆
多叉树
B-树
B-树(balance tree)
B树是一种多路平衡查找树,它的每一个节点最多包含n个子节点,n被称为b树的阶,
B-树的高度比二叉查找树要低,在索引的层面,相当于磁盘io减少,可以提升查找性能。
例如:mongoDB的索引就是用了B-树的数据结构。
Alex:
1.B-树并不是一个二叉树,而是多叉树。
2.B-树的每个节点中包含了多个元素,并且元素是从小到大排列。
3.叶子节点中还是左小右大,中间则是被包含的关系。
4.B-树的插入特别麻烦,会造成多节点连锁反应,但保证了自平衡,高度相对较小。
B-树的删除需要左旋。
5.节点中的元素多也不怕,因为每个节点的大小与磁盘页大小相同,
磁盘读取数据有预读的功能,可以把一个节点里的所有元素都读出来,在内存层面的比较是相当快的。
一个m阶的b树(下面的k相当于是一个临时变量):
1.根节点至少有2个子节点。
2.每个中间节点都包含k-1个元素和k个子节点,其中m/2 <= k <= m
(例如4阶的B-树,中间节点最多包含4个子节点,3个元素,最少包含2个子节点,1个元素)
所以这里是不是应该改成ceil(m/2),向上取整?
3.每一个叶子节点都包含k-1个元素,其中m/2 <= k <= m.
4.所有的叶子节点都位于同一层。
5.每个节点中的元素从小到大排序,节点当中k-1个元素正好是k个孩子包含的元素的值域划分。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Jr34IlRU-1684831719316)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p376)]
B+树
B+树是B-树的一种变体,有着比B-树更高的查询性能。
- 有k个子节点的中间节点包含有k个元素(B-树中是k-1个元素),每个元素不保存数据,只用来做索引,所有数据都保存在叶子节点上。
- 所有的叶子节点中包含了全部元素的信息,以及带有指向下一个叶子节点的指针,形成了一个有序链表,且叶子节点本身依关键字的大小自小而大顺序连接。
- 所有的中间节点元素都同时存在于叶子节点,在叶子节点元素中是最大或最小的元素。
- 根节点中的最大元素就是整个B+树的最大元素。
- 卫星数据,数据库索引元素所指向的数据库中的某一行数据记录,在B-树中,中间节点与叶子节点都带有卫星数据,
而在B+树中,只有叶子节点带有卫星数据,中间节点只是索引,没有任何数据关联。
在数据库的聚集索引中,叶子节点直接包含卫星数据,在非聚集索引中,叶子节点带有指向卫星数据的指针。
那么问题来了,什么是聚集索引?什么是非聚集索引?要写在自己的文章中。
相对于B-树的优势:
- B+树的中间节点没有卫星数据,所以同样大小的磁盘页可以容纳更多的节点元素。
在数据量相同的情况下,B+树比B-树更加矮胖,因此查询时的IO更少。 - B+树每一次查询都必须落在叶子节点上,保证了每一次查找都是稳定的,而B-树具有不稳定性。
(试想一下,如果一个数据库查询,有时候执行10ms,有时候执行100ms,不如每次都执行30ms) - B+树的范围查询,可以使用有序链表遍历,更加高效,而B-树则只能使用复杂的中序遍历。
图
在数据结构中,图(Graph)是由一组节点(Vertex)和一组边(Edge)组成的一种数据结构。
节点表示图中的实体,边表示节点之间的关系。
图可以用 G=(V,E) 表示,其中 V 表示节点的集合,E 表示边的集合。
如果边有方向,称为有向图(Directed Graph),
如果边没有方向,则称为无向图(Undirected Graph)。
图可以用多种方式来表示,
最常见的方式是使用邻接表(Adjacency List)或邻接矩阵(Adjacency Matrix)。
邻接表用一个数组来存储每个节点的相邻节点列表,
对于有向图,每个节点都会有一个出边列表和一个入边列表;
邻接矩阵用一个二维数组来表示节点之间的关系,
数组中的元素表示两个节点之间是否有边相连,如果有,则为 1,否则为 0。
图可以用来解决许多实际问题,比如路线规划、社交网络分析、网络安全等。
在算法设计中,图论也是一个重要的分支,
许多经典的算法和数据结构都基于图的概念,
比如最短路径算法、最小生成树算法、拓扑排序算法、网络流算法等等。
因此,学习图论对于掌握算法和数据结构的核心概念非常重要。
图是由一系列节点和边组成的数据结构,其中节点代表图中的对象,
边代表两个节点之间的关系。
图是一种复杂的数据结构,可以用于模拟各种实际问题,
如网络,地图等。图中的节点和边没有固定顺序。
数据结构中的图是一种抽象的数学模型,表示对象之间的关系,
通常用于描述网络结构。
它由节点(也称为顶点)和边组成,边表示两个节点之间的关系。
图论是一门研究图的学科,研究图的概念、性质、算法等。
它是数学、计算机科学和工程学中的一个重要领域,
在网络、图像处理、遗传学、社会网络分析等领域有着广泛的应用。
import java.util.*; // 图的节点类 class GraphNode { int val; List<GraphNode> neighbors; GraphNode(int val) { this.val = val; this.neighbors = new ArrayList<>(); } } // 有向图类 class DirectedGraph { List<GraphNode> nodes; DirectedGraph() { this.nodes = new ArrayList<>(); } // 添加节点 public void addNode(GraphNode node) { nodes.add(node); } // 添加边 public void addEdge(GraphNode from, GraphNode to) { from.neighbors.add(to); } // 深度优先搜索遍历 public void dfs(GraphNode node, Set<GraphNode> visited) { if (node == null || visited.contains(node)) { return; } visited.add(node); System.out.print(node.val + " "); for (GraphNode neighbor : node.neighbors) { dfs(neighbor, visited); } } } public class Main { public static void main(String[] args) { // 创建节点 GraphNode node0 = new GraphNode(0); GraphNode node1 = new GraphNode(1); GraphNode node2 = new GraphNode(2); GraphNode node3 = new GraphNode(3); // 创建图 DirectedGraph graph = new DirectedGraph(); graph.addNode(node0); graph.addNode(node1); graph.addNode(node2); graph.addNode(node3); // 添加边 graph.addEdge(node0, node1); graph.addEdge(node0, node2); graph.addEdge(node1, node2); graph.addEdge(node2, node0); graph.addEdge(node2, node3); graph.addEdge(node3, node3); // 深度优先搜索遍历 Set<GraphNode> visited = new HashSet<>(); System.out.print("DFS Traversal: "); graph.dfs(node2, visited); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
最短路
最小生成树
网络流建模
复合型
[散列表/哈希表]
哈希表通常是由数组和链表组成的。
哈希表使用哈希函数将键映射到数组的某个位置,
如果发生冲突(即两个不同的键被映射到同一个位置),
则使用链表将冲突的元素链接在一起。
这种组合的数据结构提供了一种高效的方法,
可以在O(1)的时间复杂度内执行插入、查询和删除操作。
散列表是一种特殊的数组,
它利用一个哈希函数将数据映射到一个固定的数组索引,
然后在该位置存储数据。
通过将数据映射到哈希表中的桶来组织数据,
从而实现快速查询和插入操作。
由于散列表内部的元素没有固定顺序,并且仅仅与哈希函数的结果相关,
因此散列表不属于线性表数据结构。
散列表具有快速查找,插入,删除操作的特点,
因此常用于解决查找问题和存储问题等。
哈希表通过使用散列函数将键映射到数组中的桶,
从而实现快速查找和插入操作。
它允许您以 O(1) 的复杂度在表中查找、插入和删除元素。
哈希表是一种基于哈希函数实现的数据结构,
它使用关键字(key)和值(value)的映射关系进行快速查找。
哈希表中的元素是通过哈希函数映射到一组桶中的,
桶之间没有顺序关系,
它可以实现非常快速的查找和插入操作,是很多算法和数据结构的重要基础。
import java.util.HashMap; public class HashMapExample { public static void main(String[] args) { // 创建一个哈希表 HashMap<String, Integer> map = new HashMap<>(); // 向哈希表中添加键值对 map.put("A", 1); map.put("B", 2); map.put("C", 3); // 获取哈希表中的值 int value = map.get("B"); System.out.println("Value for key 'B': " + value); // 判断哈希表是否包含特定的键 boolean exists = map.containsKey("C"); System.out.println("Key 'C' exists: " + exists); // 移除哈希表中的键值对 map.remove("A"); // 输出哈希表中的所有键值对 System.out.println("All values in the map: " + map.values()); Map<Integer, String> map = new HashMap(); map.put(1, "a"); map.put(2, "b"); map.put(3, "c"); // 没有key对应的话就返回个默认值value System.out.println(map.getOrDefault(4, "x"));; System.out.println(map.getOrDefault(3, "x"));; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
[散列树/哈希树]
哈希树是一种结合了哈希表和树形结构的数据结构,
它对键值进行散列映射,以实现快速的插入、查询和删除操作。
这种数据结构也被称为散列树、散列索引树或TrieHash等。
它通过对键值进行散列,将其映射到散列表的索引位置,
以实现快速的插入、查询和删除操作。
哈希树是哈希表的变种,它将链式哈希结构改为了树形结构,
同时保留了哈希表的快速查询特点。
哈希树使用的是内存分配策略,
使得哈希树的大小可以根据存储的数据动态变化,提高了内存利用率。
同时,哈希树在索引节点上附加了红黑树或B树等数据结构,
以保证排序、查询的效率。
哈希树在数据结构领域有广泛的应用,
例如在数据库、内存数据库、计算机网络等方面。
[Trie树/字典树]
Trie树(又称字典树)是一种用于检索字符串的树形结构,
是一种哈希树的变种。Trie树以字符串为键,
它的每一个节点代表了一个字符串的一个前缀,
从根节点到某一个节点的路径所代表的字符串即为该节点的前缀。
Trie树的主要用途是检索字符串,
它可以快速的找出某个字符串是否存在于Trie树中,
同时也可以快速的找出某个前缀对应的所有字符串。
由于它具有高效的查询性能,因此在许多领域,
例如字符串匹配、字典树、自动补全等,都有广泛的应用。
算法
《算法,第4版》
https://algs4.cs.princeton.edu/
[常用/常见]算法:
递归;- 排序;
- [二分算法/二分查找];
- 搜索;
- 哈希算法;
回溯算法;贪心算法;分治算法;动态规划;- 字符串匹配算法;
- 数论;
- [暴力枚举/穷举];
深度优先搜索;- 广度优先搜索;
- 滑动窗口;
- 位运算;
按照难易程度排序的最简单的10个算法:
- 枚举算法:枚举所有可能的情况,并从中选择最优解。
- 线性搜索算法:遍历列表中的每个元素,直到找到所需的元素。
- 二分搜索算法:针对已排序列表,在每次比较后将搜索范围缩小一半,直到找到所需元素。
- 冒泡排序算法:比较相邻元素的大小,并在每一轮迭代中交换它们的位置,直到整个列表排序完成。
- 选择排序算法:从列表中选择最小的元素,并将其放在第一位,然后重复这个过程,直到整个列表排序完成。
- 插入排序算法:将列表分为已排序和未排序两部分,每次将未排序的元素插入到已排序部分的适当位置。
- 斐波那契数列算法:递归或迭代生成斐波那契数列。
- 最大子序列和问题算法:在列表中查找和最大的子序列。
- 深度优先搜索算法:从根节点开始,沿着一条路径一直走到底,然后返回到前一个节点,并继续搜索。
- 广度优先搜索算法:从根节点开始,一层一层地搜索所有可能的路径,直到找到所需元素。
算法复杂度
我们用算法需要执行的时间来衡量1个算法的复杂度,
表示为:T(n)。
n is the size of the input.
T(n) is the time it takes to run on inputs of size n.
It may take different times for different inputs of the same size n.
In general we mean the worst-case running time.
(Sometimes we’re interested in the average running time.)
We don’t mean exact running time (that depends on the implementation and machine)
but a measure of the number of elementary computation steps.
How to measure input and time?
Strictly speaking we should measure:
• input size by the number of bits the input takes in memory
• running time by the number of basic hardware operations executed
In complexity theory we’re usually more relaxed
• input size is often measured by memory locations, for example lists are measured by their lengths, trees by the number of nodes
• running time is measured by assuming that certain elementary operations (for example arithmetic, logical, pointer operations) take constant time (which is usually false!)
Important is not the exact running time, but the Complexity Class: the algorithms runs in linear, or quadratic, … or exponential time
The notation f (n) = O(g(n)) intuitively means that the function f (n) grows at most as g (n)
时间复杂度
时间复杂度是计算算法执行时间的一种度量方式。
它描述了算法随着输入数据规模的增长,算法的执行时间将如何变化。
通常,我们使用大 O 复杂度表示法来表示一个算法的时间复杂度,
例如,O(n) 表示该算法的时间复杂度随着输入数据规模 n 的增长而线性增长。
算法的时间复杂度对算法的效率有着重要的影响,
因此,选择合适的算法以及优化算法的实现是软件工程中非常重要的。
时间复杂度是衡量[代码/算法]好坏的重要指标,
代码功能实现了还不够,还要看时间复杂度是不是很高。
时间复杂度是描述算法执行时间的一个函数,
类似于一个耗时的趋势,并不代表具体值。
衡量[代码/算法]好坏的指标:
- [运行时间/运行次数];
- 占用空间;
2段代码运行相同的功能需要时间和内存:
A代码运行一次需要10毫秒,内存5MB。
B代码运行一次需要1秒,内存500MB。
显然,B的代码要比A差的多。
虽然我们在算法运行前,
无法准确的估算出代码运行所花时间,
但我们可以估算出代码的执行次数。
我们把算法需要执行的运算次数,用输入大小为n的函数来表示,即:T(n)。
大写的N,代表某个特定数值。
小写的n,代表函数的变量。
一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
执行次数是常量的,T(n) = 2:
void do1(int n){
System.out.println("执行一次");
System.out.println("执行一次");
}
- 1
- 2
- 3
- 4
执行次数是线性的,一般包含非嵌套循环,随着问题规模n的扩大,对应执行次数呈直线增长,T(n) = 2n:
void do2(int n){
for(int i = 0 ; i < n ; i++){
System.out.println("执行一次");
System.out.println("执行一次");
}
}
- 1
- 2
- 3
- 4
- 5
- 6
执行次数是对数的(对数用log表示),以2为底,例如:log8 = 3,T(n) = 3logn:
void do3(int n){
for(int i = 1; i < n ; i *= 2){
System.out.println("执行一次");
System.out.println("执行一次");
System.out.println("执行一次");
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
执行次数是平方的,T(n) = n^2:
void do4(int n){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
System.out.println("执行一次");
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
执行次数是一个多项式的,用到等差数列求和公式,T(n) = 0.5n^2 + 0.5n:
void do5(int n){ for(int i = 0; i < n; i++){ for(int j = 0; j < i; j++){ System.out.println("执行一次"); } System.out.println("执行一次"); } } void do6(int n){ /** * 当 i = 0 时,内循环执行 n 次运算,当 i = 1 时,内循环执行 n - 1 次运算……当 i = n - 1 时,内循环执行 1 次运算。 所以,执行次数 T(n) = n + (n - 1) + (n - 2)……+ 1 = n(n + 1) / 2 = n^2 / 2 + n / 2。 根据上文说的大O推导法可以知道,此时时间复杂度为 O(n^2)。 * **/ for(int i = 0; i < n; i++){ for(int j = i; j < n; j++){ System.out.println("执行一次"); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
假设n=3,则共执行6次:
- 当i=0时,外循环执行1次,内循环执行0次,共1次;
- 当i=1时,外循环执行1次,内循环执行1次,共2次;
- 当i=2时,外循环执行1次,内循环执行2次,共3次;
等差数列求和公式为:S = n/2 * (a1 + an)。
数列头:1
数列尾:n
n/2 * (1 + n) = 0.5n + 0.5n^2
有了基本操作执行次数的函数T(n),
是否就可以分析和比较一段代码的运行时间了呢?
还是有一定的困难。
比如算法A的相对时间是T(n) = 100n,
算法B的相对时间是T(n) = 5n^2,
这两个到底谁的运行时间更长一些?
这就要看n的取值,随着n的变化,两个算法的执行次数会可能会发生逆转。
所以,这时候有了渐进时间复杂度(asymptotic time complectiy)的概念,官方的定义如下:
若存在函数f(n),使得当n趋近于无穷大时,
T(n) / f(n)的极限值为非零常数,
则称f(n)是T(n)的同数量级函数。
记作T(n) = O(f(n)),称O(f(n)),
为算法的渐进时间复杂度,简称时间复杂度。
渐进时间复杂度用大写O来表示,
所以也被称为大O表示法。
得到执行次数函数T(n)后,如何推导时间复杂度?
如果执行次数是常数量级,用1表示,因为常数对坐标轴中函数的曲线波动影响较小,如果函数中不仅存在常数,则把常数省略;只保留时间函数中的最高阶项(最高次幂),因为低阶项对坐标轴中函数的曲线波动影响较小;如果最高阶项存在,则省去最高阶项前面的系数,因为系数对坐标轴中函数的曲线波动影响较小;- 要运算到不能再运算为止,例如:n * n还可以转化成n^2;
例如:
- T(n) = 2,只有常数量级,转化为:T(n) = O(1);
- T(n) = 2n,最高阶项为2n,省去系数2,转化为:T(n) = O(n);
- T(n) = 3logn,最高阶项为3logn,省去系数3,转化为:T(n) = O(logn);
- T(n) = n^2,转化为:T(n) = O(n^2);
- T(n) = 0.5n^2 + 0.5n,最高阶项为0.5n^2,省去系数0.5,转化为:T(n) = O(n^2);
分类:
| 时间复杂度 | 例子 | 描述 |
|---|---|---|
| O(1) | 12345 | 常数阶 |
| O(logn) | 2logn+4 | 对数阶 |
| O(n) | 2n + 8 | 线性阶 |
| O(nlogn) | 3n + 4nlogn + 13 | 线性对数阶 |
| O(n^2) | 3n^2 + 4n + 5 | 平方阶 |
| O(n^3) | n^3 + 5n^2 + 8 | 立方阶 |
| O(n^k) | n^15 | k方阶,一般控制k的大小,否则就和指数阶一样了 |
| O(2^n) | 2^n + 8 | 指数阶,性能差 |
从[代码/算法]中推导出T(n)是困难的,
相当于我们需要拥有[把一堆代码抽象成一个数学函数]的能力。
一些推导规律:
- 从内向外分析,从最深层开始分析。如果遇到函数调用,要深入函数进行分析;
- 一重循环则时间复杂度为O(n),如果循环体内的时间复杂度为O(m),则总共为O(m * n);
- 二重循环默认为O(n2),三重循环为O(n3),前提是外层与内层循环都循环n次;
- 多重循环嵌套,由里向外分析,假设最里层循环体内的时间复杂度为O(n),每个循环的循环次数分别为:a,b,c,则总共为O(n * a * b * c);
- 二分为O(logn),例如:快速幂、二分查找;
- for循环套一个二分,为O(nlogn);
- 对于if语句,总时间复杂度等于其中[时间复杂度最大的路径]的时间复杂度。
我们查找一个有n个随机数字数组中的某个数字,
最好的情况是第一个数字就是,那么算法的时间复杂度为O(1),
但也有可能这个数字就在最后一个位置,那么时间复杂度为O(n)。
平均运行时间是期望的运行时间。
最坏运行时间是一种保证。在应用中,这是一种最重要的需求,
通常除非特别指定,我们提到的运行时间都是最坏情况的运行时间。
https://www.cnblogs.com/huangbw/p/7398418.html
https://blog.csdn.net/u012617661/article/details/80135019
https://blog.csdn.net/sustzc/article/details/80612758
https://blog.csdn.net/liao_hb/article/details/81029536
https://baike.baidu.com/item/%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6/1894057?fr=aladdin
https://blog.csdn.net/u013467442/article/details/53411257
未完待续
空间复杂度
转自:https://www.jianshu.com/p/88a1c8ed6254
我们在写代码时,完全可以用空间来换去时间。
举个例子说,要判断某年是不是闰年,你可能会花一点心思来写一个算法,
每给一个年份,就可以通过这个算法计算得到是否闰年的结果。
另外一种方法是,事先建立一个有2050个元素的数组,
然后把所有的年份按下标的数字对应,如果是闰年,
则此数组元素的值是1,如果不是元素的值则为0。这样,
所谓的判断某一年是否为闰年就变成了查找这个数组某一个元素的值的问题。
第一种方法相比起第二种来说很明显非常节省空间,
但每一次查询都需要经过一系列的计算才能知道是否为闰年。
第二种方法虽然需要在内存里存储2050个元素的数组,
但是每次查询只需要一次索引判断即可。
这就是通过一笔空间上的开销来换取计算时间开销的小技巧。
到底哪一种方法好?其实还是要看你用在什么地方。
定义:
算法的空间复杂度通过计算算法所需的存储空间实现,
算法的空间复杂度的计算公式记作:S(n)=O(f(n)),
其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
通常,我们都是用“时间复杂度”来指运行时间的需求,
是用“空间复杂度”指空间需求。
当直接要让我们求“复杂度”时,通常指的是时间复杂度。
显然对时间复杂度的追求更是属于算法的潮流!
在数据结构与算法中,
空间复杂度是指算法在执行过程中所需要的内存空间大小,
通常用大O表示法来描述。
空间复杂度与时间复杂度一样,也是衡量算法效率的重要指标之一。
一个算法的空间复杂度取决于它所需要的存储空间大小,
这个大小通常与输入数据规模有关。
在进行算法设计时,需要尽量优化空间复杂度,避免无谓的内存浪费。
在实际应用中,空间复杂度较高的算法可能会因为内存不足而无法运行,
因此空间复杂度也是算法设计中需要考虑的重要因素之一。
当你编写一个算法时,它需要占用计算机内存的一定量空间来存储数据结构和中间结果。这个算法所需要的空间大小,就是空间复杂度。举个例子,假设你需要编写一个算法来解决某个问题,你设计的算法需要使用一个大小为n的数组来存储中间结果,那么它的空间复杂度就是O(n)。如果你使用了递归,递归深度为k,每次递归需要开辟一个大小为m的数组,那么它的空间复杂度就是O(km)。另外,还有一些空间复杂度比较特殊的算法,例如原地排序算法(如快速排序和堆排序),它们只需要很少的额外空间,空间复杂度为O(1)。
未完待续
基础算法问题
全排列问题
全排列问题是指对一个给定的序列(或者是集合),
求出该序列所有可能的排列方案。
比如说,对于一个序列 [1, 2, 3],
它的全排列有三个: [1, 2, 3]、[1, 3, 2] 和 [2, 1, 3]。
这个问题常见于算法设计和其他相关领域,
主要用于搜索和组合数学等领域。
爬楼梯问题
背包问题
“背包"指的是一类问题,通常称为"0/1背包"或"完全背包”。
它是一个典型的动态规划问题,也是计算机科学中一个常见的问题。
在背包问题中,有一个固定容量的背包,和一些物品,
每个物品有一个重量和一个价值。
问题是如何选择一些物品,
使得这些物品的重量总和不超过背包容量,并且总价值最大。
八皇后问题
八皇后问题是一个经典的问题,是回溯算法的典型案例。
八皇后问题是指在8×8的国际象棋棋盘上放置八个皇后,
使得任意两个皇后都不在同一行、同一列或同一对角线上(如果皇后在中间的话,会有4条对角线)。
总共有92种不同的放置方案。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3x7sZm8X-1684831719318)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4031)]
八皇后问题的解决方案是一种回溯算法,
它尝试在每一行都放置一个皇后,
并且检查每一行放置的皇后是否与前面放置的皇后冲突。
如果没有冲突,程序将继续执行下一行。
如果冲突,则回溯并在当前行放置另一个皇后,
直到找到可行的解决方案。
基础算法思想
枚举
千万不要误会,这里的枚举与Java里的枚举完全不是一个东西。
在数据结构与算法中,枚举(Enumeration)是一种算法思想,
它通过遍历所有可能的情况来解决问题。
而在Java中,枚举(Enum)是一种特殊的数据类型,
它表示一组固定的常量值。
枚举,Enumeration,是一种常见的算法思想,
它通过遍历所有可能的情况来解决问题。
枚举通常用于在有限范围内搜索特定的解,
例如在密码破解中破解密码、在游戏中寻找最优策略等。
枚举的基本思路是通过循环遍历所有可能的情况来搜索解决方案。
例如,在密码破解中,可以使用一个循环来遍历所有可能的密码组合,
直到找到正确的密码为止。
尽管枚举算法通常可以找到解决方案,
但由于它必须遍历所有可能的情况,因此通常需要很长时间来执行。
此外,在搜索空间很大时,枚举可能不太实用。
因此,在实际应用中,枚举通常与其他算法一起使用,
以便在搜索空间较小时找到最优解决方案。
需要注意的是,枚举算法不适用于所有类型的问题。
对于某些问题,搜索空间可能太大,无法通过枚举来解决。
在这种情况下,需要使用其他算法来寻找最优解决方案。
枚举算法,Enumeration algorithm,是一种穷举的方法,
通过不断地枚举每一种情况来解决问题。
枚举算法通常在求解组合问题,搜索最优解等方面被广泛使用。
枚举算法需要耗费大量的时间和计算资源,
因此在实际应用中需要注意问题的规模。
枚举法(Brute Force)是指将所有可能的情况枚举出来,
再判断是否满足条件,如果满足条件则记录下答案。
这是一种简单粗暴的解决问题的方法,最简单的例子就是穷举法,
例如对于一个数的n次方的答案,将每一位的n次方暴力穷举。
这种方法的复杂度很高,但对于一些简单的问题,
有时也是一种不错的解决方法。
穷举法和枚举法是同一个概念,
表示通过试错、枚举来寻找某种问题的解决方案。
递归
在计算机科学中,递归指的是一种解决问题的方法,
它把一个问题分解为规模更小但本质上与原问题相同的子问题,
逐个解决子问题,最后将它们合并成原问题的解。
递归需要满足两个条件:
- [终止条件/停止条件/基准情况]:递归必须有一个停止条件,否则递归将无限进行下去;
- 递推公式:递推公式指的是把原问题分解成规模更小的子问题的公式,一般写在return处;
是的,递归是一种常见的编程技巧,递归调用自身的函数时需要设置停止条件,否则会导致无限递归,最终耗尽系统的栈空间,引发栈溢出错误。需要注意递归调用的层数不要过深,否则也会出现类似的问题。
递归可以用来解决许多问题:
树的遍历;- 图的搜索;
- 分治算法;
- 动态规划;
在实现递归时,需要注意避免出现栈溢出等问题。
例如:输入一个整数n,输出n的阶乘:
public class Factorial { public static int factorial(int n) { if (n == 0 || n == 1) { // 基准情况 return 1; } else { // 递推公式 return n * factorial(n - 1); } } public static void main(String[] args) { int n = 5; System.out.println(factorial(n)); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
贪心算法
[贪心算法]是一种在每一步选择中都选择当前最优(最优解)的算法,
并且假设在未来的步骤中能够维持最优性质,以达到全局最优解的算法。
它的目的是通过局部最优解得到全局最优解。
下面的代码演示了一个简单的[背包问题],它有三个物品,
每个物品都有2个属性:重量、价值。
最大价值是在所有物品中选择价值/重量比最大的物品,
直到背包装满为止。
代码中的贪心策略是将所有物品按价值/重量比排序,
然后从最优的物品开始装入背包。
import java.util.ArrayList; import java.util.Comparator; import java.util.List; public class Knapsack { static class Item { int weight; int value; Item(int weight, int value) { this.weight = weight; this.value = value; } } static int getMaxValue(int capacity, List<Item> items) { items.sort(Comparator.comparingDouble(a -> (double) a.value / a.weight)); int currentWeight = 0; int currentValue = 0; for (Item item : items) { if (currentWeight + item.weight <= capacity) { currentWeight += item.weight; currentValue += item.value; } else { int remain = capacity - currentWeight; currentValue += item.value * ((double) remain / item.weight); break; } } return currentValue; } public static void main(String[] args) { List<Item> items = new ArrayList<>(); items.add(new Item(10, 60)); items.add(new Item(20, 100)); items.add(new Item(30, 120)); int capacity = 50; System.out.println(getMaxValue(capacity, items)); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
滑动窗口算法
滑动窗口,Sliding Window,是一种常用的算法技巧,
用于解决字符串或数组相关的问题,基于双指针。
它通过维护一个窗口(一般是连续的子数组或子字符串),
在数据结构中进行滑动并进行相应的操作。
滑动窗口算法通常用于解决满足一定条件的连续子序列或子数组的问题,
例如求解最小/最大值、求解和等。
它的基本思想是通过滑动窗口在数据结构中移动,
同时根据问题的要求进行窗口的扩展或收缩,
并在每次移动后更新窗口内的状态。
以下是滑动窗口算法的基本步骤:
- 初始化窗口的起始位置和结束位置;
- 判断窗口内的子序列或子数组是否满足特定的条件;
- 如果满足条件,根据问题的要求进行相应的操作;
- 向右移动窗口的起始位置或结束位置,更新窗口内的状态。
- 重复步骤2-4,直到遍历完整个数据结构。
通过不断移动窗口,滑动窗口算法能够在O(n)的时间复杂度内解决很多子序列或子数组相关的问题,相比于暴力求解的方法具有更高的效率。
需要注意的是,滑动窗口算法并不是适用于所有问题,而是针对一类特定的问题设计的算法技巧。
在使用滑动窗口算法解决问题时,
需要根据具体的问题进行窗口的扩展和收缩操作,并确保窗口的移动规则正确和高效。
public class SlidingWindowExample { public static int maxSubarraySum(int[] nums) { int windowStart = 0; // 窗口起始位置 int windowSum = 0; // 窗口内元素的和 int maxSum = Integer.MIN_VALUE; // 最大子数组和 for (int windowEnd = 0; windowEnd < nums.length; windowEnd++) { // 扩展窗口:将当前元素添加到窗口内 windowSum += nums[windowEnd]; // 如果窗口内元素的和大于最大子数组和,则更新最大子数组和 if (windowSum > maxSum) { maxSum = windowSum; } // 收缩窗口:如果窗口内元素的和为负数,则从窗口起始位置开始收缩窗口 if (windowSum < 0) { windowSum = 0; windowStart++; } } return maxSum; } public static void main(String[] args) { int[] nums = {2, -5, 3, 1, -2, 4, -3}; int maxSum = maxSubarraySum(nums); System.out.println("最大子数组和为: " + maxSum); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
深度优先搜索算法与广度优先搜索算法
定义:
- 深度优先搜索算法,Depth-First Search,DFS,是一种用于图和树的遍历算法,它的核心思想是尽可能深地搜索每个分支,直到到达树的底部或者找到目标为止。它从起始节点开始遍历,沿着一条路径尽可能深入地访问节点,直到无法继续深入,然后回溯到上一个节点,沿着另一条路径继续深入访问。与广度优先搜索不同,它使用[栈]来保存遍历过程中的节点,每次从栈顶取出一个节点,访问该节点的邻居节点,然后将邻居节点压入栈顶;
- 广度优先搜索算法,Breadth-First Search,BFS,是一种用于图和树的遍历算法,它从起始节点开始遍历,逐层[向外搜索/向下搜索],先访问起始节点的所有[邻居节点/子节点],然后依次访问每个[邻居节点/子节点]的所有未访问过的[邻居节点/子节点],以此类推,直到找到终点或所有节点都被遍历。广度优先搜索算法使用[队列]来保存将要遍历的节点,先将[根节点/起始节点]加入[队列],然后从队列的头部取出一个节点,第一次就是取出[根节点/起始节点],再访问该节点的所有[邻居节点/子节点],然后将[邻居节点/子节点]加入[队列]尾部,再从队列的头部取出一个节点,直到找到目标为止。
可以用于对树的每一层(横向)进行操作;
两种算法的主要区别在于遍历的顺序。
DFS每次遍历都是尽可能深入,
直到到达叶子节点,再回溯到上一层继续搜索,
而BFS是从起点开始,按层遍历图中的所有节点。
DFS例子
以下是一个简单的例子,展示了深度优先搜索算法是如何遍历一个无向图的。
0
/ \
1 - 2
\ /
3
- 1
- 2
- 3
- 4
- 5
在上图中,数字表示节点的编号,线表示节点之间的边。
我们从节点0开始进行深度优先搜索遍历,
遍历过程中使用[栈]来保存待访问的节点,
初始时将起始节点0放入[栈]中:
Stack: [0]
Visited: [0]
- 1
- 2
然后从栈顶取出节点0,访问它的邻居节点1和2,并将它们压入栈顶:
Stack: [1, 2]
Visited: [0, 1, 2]
- 1
- 2
接下来从栈顶取出节点2,访问它的邻居节点1和3,但由于节点1已经被访问过了,因此不再重复访问。将邻居节点3压入栈顶:
Stack: [1, 3]
Visited: [0, 1, 2, 3]
- 1
- 2
接下来从栈顶取出节点3,它没有任何邻居节点,因此将从栈中弹出它,接下来回溯到上一个节点1,访问它的邻居节点0和2,但由于它们都已经被访问过了,因此不再重复访问:
Stack: [1]
Visited: [0, 1, 2, 3]
- 1
- 2
最后从栈顶取出节点1,它没有其他邻居节点,因此遍历结束。
可以看出,深度优先搜索算法按照深度优先的方式遍历图,
最终遍历了整个图,并输出了遍历顺序。
BFS例子
以下是一个简单的例子,展示了广度优先搜索算法是如何遍历一个无向图的。
0
/ \
1 - 2
\ /
3
- 1
- 2
- 3
- 4
- 5
在上图中,数字表示节点的编号,线表示节点之间的边。
我们从节点 0 开始进行广度优先搜索遍历,
遍历顺序应该为 0、1、2、3。
遍历过程中使用[队列]来保存待访问的节点,
初始时将起始节点 0 放入[队列]中:
Queue: [0]
Visited: [0]
- 1
- 2
然后从队列头部取出节点 0,
访问它的邻居节点 1 和 2,并将它们加入[队列]尾部:
Queue: [1, 2]
Visited: [0, 1, 2]
- 1
- 2
接下来从队列头部取出节点 1,访问它的邻居节点 0 和 3,
但由于节点 0 已经被访问过了,因此不再重复访问。
将邻居节点 3 加入队列尾部:
Queue: [2, 3]
Visited: [0, 1, 2, 3]
- 1
- 2
现在从队列头部取出节点 2,访问它的邻居节点 0 和 3,
但由于它们都已经被访问过了,因此不再重复访问:
Queue: [3]
Visited: [0, 1, 2, 3]
- 1
- 2
最后从队列头部取出节点 3,它没有任何邻居节点,因此遍历结束。
可以看出,广度优先搜索算法按照与起始节点的距离逐层扩展,
最终遍历了整个图,并输出了遍历顺序。
分治算法
分治算法,Divide and conquer algorithm,
是一种利用分治的思想,将一个大问题分成两个或更多的子问题,
再把子问题分成更小的问题,直到最后子问题可以简单的直接求解,
原问题的解即子问题的解的合并。
分治算法通常用于处理大规模问题,是一种很有效的算法。
常见的例子有:快速排序,归并排序,汉诺塔问题等。
以下是一个使用分治算法实现快速排序,
其中利用分治思想将数组划分为两个子数组,
然后对子数组进行递归排序。
快速排序的核心思想是选取一个枢纽元素,
将数组划分为两个子数组,
使得左子数组中的所有元素都小于等于枢纽元素,
右子数组中的所有元素都大于等于枢纽元素。
然后对左右子数组分别进行递归排序,最终得到排序好的数组。
public class QuickSort { public static void quickSort(int[] arr, int left, int right) { if (left < right) { // 划分子数组 int partitionIndex = partition(arr, left, right); // 递归排序左子数组 quickSort(arr, left, partitionIndex - 1); // 递归排序右子数组 quickSort(arr, partitionIndex + 1, right); } } private static int partition(int[] arr, int left, int right) { // 选取中间元素为枢纽元素 int pivot = arr[left + (right - left) / 2]; int i = left; int j = right; // 对数组进行划分 while (i <= j) { while (arr[i] < pivot) { i++; } while (arr[j] > pivot) { j--; } if (i <= j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; i++; j--; } } // 返回枢纽元素的下标 return i; } public static void main(String[] args) { int[] arr = {5, 2, 9, 1, 5, 6}; quickSort(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
回溯算法
回溯算法,Backtracking Algorithm,是一种分治算法,
用于在有限的搜索空间内寻找所有可行的解。
它是一种通用的解决组合优化问题的算法,
可以适用于找出所有的可能的解,或者在找到第一个合法解时终止。
回溯算法的基本思想是:
在当前层次选择一个可行的解,并在下一层继续试探下一个可行解。
如果在下一层无法找到任何合法解,则回溯到上一层,
选择另一个可行解继续试探。
回溯算法是一种递归的算法,用于求解在一组可能的解中找出所有符合条件的解的问题。
在八皇后问题中,回溯算法的基本思路是从第一行开始尝试放置皇后,
当某一行不能放置皇后时,回溯到上一行重新尝试,
直到找到所有符合条件的解或者所有可能的解都已经被尝试完毕。
使用回溯算法求解八皇后问题的时间复杂度为 O(n!),
其中 n 是皇后的数量。因为在最坏情况下,需要枚举所有的可能性,
而八皇后问题的解空间大小为 8! = 40320,因此时间复杂度非常高。
这个过程在直到找到最终的合法解,或者所有的搜索空间都已被搜索过为止。
回溯算法常常用于解决NP问题(如N-皇后问题,八数码问题等),
它是一种高效的算法,其时间复杂度取决于找到合法解的数量。
https://mp.weixin.qq.com/s/puk7IAZkSe6FCkZnt0jnSA
递归回溯,本质上是一种[枚举法]。
这种方法从棋盘的第一行开始尝试摆放第一个皇后,摆放成功后,递归一层,再遵循规则在棋盘第二行来摆放第二个皇后。
如果当前位置无法摆放,则向右移动一格再次尝试,
如果摆放成功,则继续递归一层,摆放第三个皇后…
如果某一层看遍了所有格子,都无法成功摆放,则回溯到上一个皇后,
让上一个皇后右移一格,再进行递归。
如果八个皇后都摆放完毕且符合规则,那么就得到了其中一种正确的解法。
public class TempClass { public static void main(String[] args) { QueenProblem.backtrack(0); System.out.println("共有" + QueenProblem.count + "种合法的放置方案。"); } } class QueenProblem { static final int N = 8; static int[] x = new int[N]; // x[i]表示第i行皇后的放置列 // x数组用来记录每一行皇后的位置,比如x[3]=5表示第3行的皇后在第5列。 static int count = 0; // 记录满足条件的方案数 // 检查当前位置是否满足条件,一组操作时,每次进来row是固定的 static boolean check(int row, int column) { System.out.println("执行check,row="+row+",column="+column); for (int i = 0; i < row; i++) { System.out.println("仔细检查第"+i+"行,第"+column+"列。"); // 检查行冲突,每一行的列,只要是跟被占的列冲突就不行。 if (x[i] == column) { return false; } // 检查对角线冲突,要查询的行与已被占的行间距 = 要查询的列与已被占的列间距,意味着是斜线,可以自己画个图。 if (Math.abs(x[i] - column) == Math.abs(i - row)) { return false; } } return true; } // 递归搜索所有的放置方案,如果找到了一种合法的方案就把计数器加一。 static void backtrack(int row) { System.out.println("执行backtrack,row="+row); // 已经搜索到最后一行,说明已经找到一种合法的方案 if (row == N) { count++; return; } for (int i = 0; i < N; i++) { // 循环检查每个列,看当前行的哪个列符合标准 if (check(row, i)) { x[row] = i; // 把当前皇后放在当前行的第i列 backtrack(row + 1); // 回溯 x[row] = 0; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
倍增算法
倍增算法,Double Dividing Algorithm,
是一种分治算法的变形。
倍增算法通过不断地将问题的规模减半来解决问题,
从而提高算法的效率。
倍增算法常用于解决有关序列、树等数据结构的问题,
特别是处理有关序列上的查找、搜索问题时,
其时间复杂度通常为 O(log n),非常高效。
动态规划
动态规划问题一直是大厂面试时最频繁出现的算法题,
主要原因在于此类问题灵活度高,思维难度大,没有很明显的套路做法。
动态规划,Dynamic Programming,
是一种在数学、计算机科学、经济学等领域中应用的优化方法。
它是一种分阶段求解决策问题的数学思想,
通过将问题分解为若干个子问题,
再通过子问题的解推导出问题的解(大事化小,小事化了),
从而避免重复计算,提高算法的效率。
将一个复杂的问题分阶段进行简化,逐步转化成简单问题。
它通常用于解决最优化问题,即在满足某些限制条件下,找到最优解的问题。
动态规划将问题分解成若干个阶段,每个阶段需要做出一次决策,
并基于前面的决策结果,推导出当前阶段的最优解。
通过对每个阶段的最优解进行存储,
动态规划能够避免重复计算,提高计算效率。
动态规划通常需要满足以下3个条件:
- 最优子结构性质:一个问题的最优解包含其子问题的最优解。也就是说,问题可以分解成若干个子问题,并且每个子问题的最优解能够组合成原问题的最优解;
- 重叠子问题:问题可以分解成若干个重叠的子问题。也就是说,问题的每个阶段可能需要计算相同的子问题;
- 无后效性:一个问题的当前状态能够完全包含之前的决策结果,并且对后续的决策没有影响。也就是说,一个状态的转移只能由它之前的状态推导出来;
动态规划算法通常包含两个主要步骤:状态设计和状态转移方程。
状态设计定义了问题的状态,即在每个阶段需要计算和存储的信息。
状态转移方程则定义了如何从前一个状态推导出当前状态的信息。
通常,状态转移方程可以通过对问题的最优子结构性质进行推导得出,
也可以通过暴力枚举法推导得出,并通过存储中间结果避免重复计算。
动态规划算法中,递归的函数就像是《盗梦空间》中的"梦中梦",
一层套一层,又渐次展开,很难整体把控。
动态规划算法的重点是抓住[状态转移公式/状态转移方程],
只处理两个状态之间的过渡和[边界条件],慢慢"大事化小,小事化了";
https://mp.weixin.qq.com/s/3h9iqU4rdH3EIy5m6AzXsg
https://mp.weixin.qq.com/s/RqkrgzQsulFc-PHmB3znmA
https://mp.weixin.qq.com/s/YeebGBcc5dv2fRYQacgCuQ
https://mp.weixin.qq.com/s/ssLawuRYafAGd9hVyuUJIg
爬楼梯问题
例如,在[爬楼梯]问题中,
我们可以通过把最后一步拆分成两种情况来依次逐渐拆分子步骤。
问题建模:
F(1) = 1;
F(2) = 2;
F(n) = F(n-1) + F(n-2)(n>=3)
三个重要概念:
F(10) = F(9) + F(8),则F(9)和F(8)是F(10)的[最优子结构];F(1)和F(2)是问题的[边界],可以直接得出结果,无需再进行简化,如果一个问题没有边界,将永远无法得到有限的结果;F(n) = F(n-1) + F(n-2)是阶段与阶段之间的[状态转移公式/状态转移方程],它决定了问题的当前阶段与下一阶段的关系;
求解问题:
方法1,递归求解,时间复杂度为O(2^N):
int getClimbingWays(int n){
if(n < 1){
return 0;
}
if(n == 1 || n == 2){
return n;
}
return getClimbingWays(n-1) + getClimbingWays(n-2);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
方法2,备忘录算法,时间复杂度为O(N),空间复杂度为O(N):
方法1中存在大量重复计算的工作量,为了优化步骤,
我们可以使用缓存,先创建一个哈希表,
每次把不同参数的计算结果存入哈希,当遇到相同参数时,
再从哈希表中取出,从而避免重复计算。
int getClimbingWays(int n, HashMap<Integer, Integer> map){ if(n < 1){ return 0; } if(n == 1 || n == 2){ return n; } if(map.containsKey(n)){ return map.get(n); } else { int value = getClimbingWays(n-1, map) + getClimbingWays(n-2, map); map.put(n, value); return value; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
方法3,动态规划求解,时间复杂度为O(N),空间复杂度为O(1),
逆向思维,从下往上,不去递归,用循环代替:
int getClimbingWays(int n){ if(n < 1){ return 0; } if(n == 1 || n == 2){ return n; } int a = 1; int b = 2; int temp = 0; for(int i = 3; i <= n; i++){ temp = a + b; a = b; b = temp; } return temp; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
国王和金矿问题
共10名工人,
200金/3人,
300金/4人,
350金/3人,
400金/5人,
500金/5人。
建模,能根据题干推导出公式是灵魂所在:
最优子结构,第5个金矿存在挖与不挖两种选择:
- 10人4金矿的最优选择,如果不挖第5个金矿;
- (10-3)人4金矿时的最优选择,如果挖第5个金矿,会用掉一部分工人,那么前4个金矿所分配的工人数量就是[10-第5个金矿所需人数];
设:
- 金矿总数量:N;
- 工人总数量:W;
- 黄金量:G[];
- 用工量:P[];
状态转移公式:
F(5, 10) = MAX(F(4, 10), F(4, 10-P[4]) + G[4]);
边界,当只剩下一座金矿时,如果工人总数够或不够:
- 当N=1,W>=P[0]时,F(N,W) = G[0];
- 当N=1,W<P[0]时,F(N,W) = 0;
[状态转移公式/状态转移方程]:
F(N,W) = 0 (n<=1, w<p[0]);
F(N,W) = G[0] (n==1, w>=p[0]);
F(N,W) = F(N-1,W) (n>1, w<p[n-1]);(有疑问)
F(N,W) = MAX(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) (n>1, w>=p[n-1]);
方法1,排列组合,时间复杂度为O(2^N):
每一座金矿都有挖与不挖两种选择,如果有N座金矿,
排列组合起来就有2^N种选择。
对所有可能性做遍历,排除那些使用工人数超过10的选择,
在剩下的选择里找出获得金币数最多的选择。
写法略。
方法2,简单递归:
把状态转移方程式翻译成递归程序,
递归的结束的条件就是方程式当中的边界。
因为每个状态有两个最优子结构,
所以递归的执行流程类似于一颗高度为N的二叉树。
方法的时间复杂度是O(2^N)。
方法3:备忘录算法
在简单递归的基础上增加一个HashMap备忘录,用来存储中间结果。HashMap的Key是一个包含金矿数N和工人数W的对象,
Value是最优选择获得的黄金数。
方法的时间复杂度和空间复杂度相同,都等同于备忘录中不同Key的数量。
方法4:动态规划
未完待续
共10名工人,
第1座矿:400金/5人,
第2座矿:500金/5人,
200金/3人,
300金/4人,
350金/3人,
表格第一列为N的取值,第一行为W的取值,其余部分为N和W对应的黄金获得数F(N,W):
| 1个人 | 2个人 | 3个人 | 4个人 | 5个人 | 6个人 | 7个人 | 8个人 | 9个人 | 10个人 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1个矿 | 0 | 0 | 0 | 0 | 400 | 400 | 400 | 400 | 400 | 400 |
| 2个矿 | 0 | 0 | 0 | 0 | ||||||
| 3个矿 | ||||||||||
| 4个矿 | ||||||||||
| 5个矿 |
共10名工人,
第1座矿:400金/5人,
第2座矿:500金/5人,
-
只有1个矿时,第一座矿是400金/5人,因此少于5个人都没有收益,所以第1行的前几列都是0,而由于只有1个矿,来100个人也是400金收益,因此后面都是400,这个是问题的边界;
-
只有2个矿时,第二座矿是500金/5人,前面4格计算方式:W<5,F(N,W) = F(N-1,W) = 0;
-
金矿总数量:N;
-
工人总数量:W;
-
黄金量:G[];
-
用工量:P[];
F(N,W) = 0 (n<=1, w<p[0]);
F(N,W) = G[0] (n==1, w>=p[0]);
F(N,W) = F(N-1,W) (n>1, w<p[n-1]);(有疑问)
F(N,W) = MAX(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) (n>1, w>=p[n-1]);
我的思路,跟那个背包问题类似,先算出每个金矿的性价比,
再排序出高低,再把高的拿出来,
然后减少人数,等人数到0时结束。时间复杂度是O(N);
未完待续;
最长子序列?
计数问题?
[查找/搜索]
[线性搜索/线性查找/遍历查找/顺序搜索]
在数据结构与算法中,最简单的搜索算法是线性搜索(Linear Search),也被称为顺序搜索(Sequential Search)或遍历搜索(Traversal Search)。线性搜索算法的时间复杂度是O(n),其中n是要搜索的元素数量。
线性搜索算法通过遍历数组中的每个元素来查找目标元素。具体来说,它从数组的第一个元素开始,一直遍历到数组的最后一个元素,逐一比较每个元素是否与目标元素相等,如果找到目标元素则返回其位置,否则返回不存在。
虽然线性搜索算法的实现非常简单,但是当要搜索的元素数量很大时,它的时间复杂度会变得很高,效率不高。在实际应用中,通常会采用更加高效的搜索算法,如二分搜索、哈希表等。这些算法在特定条件下可以更快地找到目标元素。
[二分算法/二分查找/二分搜索/折半查找]
[二分算法/二分查找/二分搜索/折半查找],Binary Search algorithm,
是一种在有序数组或列表中查找某一特定元素的搜索算法。
该算法通过不断地将查询范围缩小一半来确定目标元素的位置,
从而降低查找时间的复杂度。
它的基本思想是:
- 每次取数组的中间元素与目标元素进行比较;
- 如果中间元素比目标元素大,则在数组的前半部分继续查找;
- 如果中间元素比目标元素小,则在数组的后半部分继续查找;
- 直到找到目标元素或者数组的前后两个指针重合为止;
二分算法的时间复杂度是O(log n),
它比线性查找的时间复杂度O(n)更优秀。
特点:
- 需要定义[左边界],[右边界],[中间元素/基准元素],3个变量;
- 循环遍历数组,每次将[左边界]向右移动,或将[右边界]向左移动;
public class BinarySearch { public static int binarySearch(int[] arr, int target) { // 左边界 int left = 0; // 右边界 int right = arr.length - 1; while (left <= right) { int mid = (left + right) / 2; if (arr[mid] == target) { return mid; } else if (arr[mid] < target) { left = mid + 1; } else { right = mid - 1; } } return -1; } public static void main(String[] args) { int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9}; int target = 5; int result = binarySearch(arr, target); if (result == -1) { System.out.println("Element not present"); } else { System.out.println("Element found at index " + result); } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
剪枝技巧
插值查找法
斐波那契查找法
用计算机程序输出斐波那契數列的前N个数是一个非常简单的问题,
许多初学者都可以轻易写出如下函数:
def fab(max):
n, a, b = 0, 0, 1
while n < max:
print b
a, b = b, a + b
n = n + 1
fab(5)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
线性索引
稠密索引
分块索引
倒排索引
排序算法
冒泡排序
Bubble Sort,基于比较的排序算法,时间复杂度均为O(n^2)。
冒泡排序通过不断交换相邻的元素来进行排序。
具体来说,它从左往右遍历数组,比较相邻两个元素的大小,
如果前一个元素大于后一个元素,则交换它们的位置。
不断进行这个比较和交换的过程,直到数组完全有序。
public static String sortArray(String params){ int temp ; String[] args = params.split(","); String result = ""; for(int x = 0;x <args.length;x++){ for(int y = x;y <args.length-1;y++){ int arg1 = Integer.parseInt(args[x]); int arg2 = Integer.parseInt(args[y+1]); if(arg2<arg1){ temp = arg2; arg2 = arg1; arg1 = temp; } args[x] = arg1+""; args[y+1] = arg2+""; } if(x==args.length-1){ result += args[x]; }else{ result += args[x]+","; } } return result; } 第二种for循环方式 int s = 0; // int[] a = new int[]{3,54,12,412,42}; // for(int i = a.length - 1;i>=1;i--){ // for(int j = 0;j<i;j++){ // if(a[j] > a[j+1]){ // s = a[j+1]; // a[j+1] = a[j]; // a[j] = s; // } // } // }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
选择排序
Selection Sort,基于比较的排序算法,时间复杂度均为O(n^2)。
选择排序通过不断选择数组中最小的元素来进行排序。
具体来说,它从左往右遍历数组,找到最小的元素,
然后将它与数组的第一个元素交换位置。
接着在剩余的未排序部分中继续寻找最小的元素,
并将它与已排序部分的后一个元素交换位置。
不断进行这个选择和交换的过程,直到数组完全有序。
快速排序
非常非常非常重要的知识点,
快速排序(Quicksort)是一种常见的基于比较的排序算法,
它是一种分治算法,通过不断地把待排序的序列分割成两个子序列,
然后对这些子序列进行递归排序,
并将小于[基准值]的元素移动到序列的左边,
大于[基准值]的元素移动到序列的右边,
最终使得整个序列有序。
在实际实现中,快速排序通常使用in-place排序方法,
即将待排序的序列直接在原数组上进行操作,避免了空间的浪费。
快速排序的时间复杂度为
O
(
n
log
n
)
O(n \log n)
O(nlogn),其中n是待排序序列的长度。
在最坏情况下,即待排序序列本身就是有序或接近有序的情况下,
快速排序的时间复杂度退化为
O
(
n
2
)
O(n^2)
O(n2)。
因此,在实际应用中,需要对快速排序进行优化,
例如随机选择基准元素、使用三数取中法选择基准元素等。
具体来说,快速排序的过程可以概括为以下3个步骤:
- 选取[基准值]:从待排序的序列中任选一个元素作为[基准值](pivot),一般选择第一个或最后一个元素;
- 划分序列:将所有小于[基准值]的元素放在[基准值]的左边,所有大于[基准值]的元素放在[基准值]的右边,而等于[基准值]的元素则可以放在任意一边,这个过程可以使[双指针]来实现;
- 递归排序:对[基准值]左右两边的子序列重复执行上述两个步骤,直到子序列长度为1或0,排序完成;
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EfnFpy11-1684831719319)(evernotecid://BCE3D193-8584-4CB1-94B3-46FF37A1AC6C/appyinxiangcom/12192613/ENResource/p4047)]
特点:
- 需要使用递归;
- 需要使用移位,将2个元素调换位置;
- 双指针,需要左右开弓,左面试了不行就试右边,谁行谁移动,都不行就调换位置;
[快速排序]和[二分查找]都是常见的算法,它们有以下相同之处:
- 都是基于分治思想的算法,都需要一个[基准元素]来进行比较;
- 都是高效的算法,可以处理大规模的数据集,时间复杂度都是 O(log n) 或 O(n log n) 级别的;
public class TempClass { public static void main(String[] args) { int[] nums = {5, 3, 6, 2, 1, 4}; quickSort(nums, 0, nums.length - 1); System.out.println(Arrays.toString(nums)); } public static void quickSort(int[] arr, int left, int right) { int a = (int)(Math.random() * 9 + 1) * 100000; System.out.println(a); if (left < right) { System.out.println(a); int pivot = partition(arr, left, right); System.out.println(a); quickSort(arr, left, pivot - 1); System.out.println(a); quickSort(arr, pivot + 1, right); System.out.println(a); } } /** * partition方法来划分序列,它采用了双指针的思想, * 先选取左边第一个元素作为基准值,然后使用 i 和 j 两个指针分别从左往右和从右往左扫描序列, * 找到需要交换位置的元素,最终将基准值放到正确的位置上。 */ private static int partition(int[] arr, int left, int right) { int pivot = arr[left]; // 选取左边第一个元素作为基准值 int i = left + 1, j = right; while (i <= j) { if (arr[i] <= pivot) { // 左边元素小于等于pivot,i右移 i++; } else if (arr[j] > pivot) { // 右边元素大于pivot,j左移 j--; } else if (i < j) { // 左边元素大于pivot,右边元素小于等于pivot,交换i和j位置的元素 swap(arr, i, j); // 交换两个元素的位置,因为既不能往左移,也不能往右移,说明2个位置是矛盾的,应该互相调转枪头 } } swap(arr, left, j); // 将pivot与j互换,因为此时j+1是大于pivot的,这样的交换是符合顺序的 return j; } private static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
归并排序
计数排序
桶排序
未完待续
插入排序
希儿排序
堆排序
跳舞链
跳舞链是一种链表排序算法,在解决大量数据的排序问题时,
它是一种有效的方法。
跳舞链是通过不断地在链表上跳跃来排序元素的。
跳舞链是对链表排序算法的优化,
它通过使用指针和移动链表中的元素来实现排序。
这个算法的特殊之处在于,它使用了两个指针,一个指针指向链表的头,
另一个指针指向链表的尾。
两个指针不断地交替移动,并在每次移动后比较两个元素的大小。
如果元素不在正确的位置,它们将被交换。
算法继续重复这个过程,直到所有元素都在正确的位置。
跳舞链是一种高效的排序算法,因为它在一次遍历中完成了排序。
这种算法在排序大量数据时特别有效。
附录1:力扣刷题
刷题!大家都重视到算法刷题对冲击大厂的重要性!
个人建议每天至少刷3道题。
刷题技巧
刷题之前,我们需要知道怎么去刷,按什么顺序刷题,应该根据需求来:
如果是为了拿大厂offer,那么在力扣上刷够大概200道经典题, 注意不是重复刷简单题,是分门别类的刷,可以先刷《剑指Offer》https://leetcode.cn/problem-list/xb9nqhhg/,再刷《热题100》https://leetcode.cn/problem-list/2cktkvj/,最后刷《前200题》https://leetcode.cn/problemset/all/;- 如果是想长期系统的学习算法,提升自己的学科素养,建议按类型刷题,
分门别类的学习、总结,有针对性的提升;
如果你有数据结构与算法基础,比如考研或者平时数据结构学的还不错,
常见数据结构与算法原理明白能够实现部分,又或者有部分刷题经验,
那么我推荐你直接顺序着刷就完了。
如果你是真的小白,那你就要为自己手动找到一条可行走的路,
那我推荐你可以按照一些专题去各个击破。
因为你是小白如果顺序刷这个题不会,学了,再刷下一题,
又学了个完全陌生的新东西,短期内学习太多比较陌生的新东西很难吸收,
很容易忘,就会陷入怎么都学不会的苦恼中。
所以你可以把刷题当成一个台阶,一层一层往上爬,
刚开始找easy简单那种a+b类型的题,
后面慢慢增加难度,
对于数据结构方面的题,
从链表开始先学透单链表、双链表、循环链表各种插入删除实现,
然后在题库中找链表相关题进行逐个攻破(链表中的也可细分链表插入、删除、反转、合并、查找、排序等等),
链表大专题之后二叉树大专题、哈希表专题等。
这样你短期内学习某一个数据结构或者算法技巧,
多去刷题巩固吸收效果比较好!
在这种情况切勿觉得简单就草草下一个,你不敲代码,
可能不会知道自己会出现什么问题。
新手也可以按此顺序:
数组;链表;哈希表;栈与队列;字符串;- 树(二叉树);
- 递归;
- 回溯算法;
- 贪心算法;
- 动态规划;
- 图;
- 其他高级数据结构;
实战练习非常重要,不经过实战练习,理论仅仅是纸上谈兵。
比如,不经过大量练习:
- 永远不会知道二分算法是多么容易出现死循环;
- 一个边界条件控制不好,程序就会显示无情的 “Time Limit Exceeded”;
- 在20分钟的调试后,或许仅仅是将 while (left <= right) 改为了 while (left < right);
程序员说到底也是手艺人,这一个字符的改动,
正是 “台上一分钟,台下十年功” 的体现,
需要在大量的练习中才能理解两者之间的不同作用。
对于初学者:
- 抄题,其实比较适合初学者的方法可以是先抄题,再把别人的解题思路推敲出来,让大脑对代码形成一种固有记忆,再去看一些解题视频,专业书籍就会感觉轻松许多。当然这是一种比较笨的方法,练习多了你的思路会被慢慢的打开。(不是盲抄,建议复盘解题思路,心领神会,否则同样达不到效果);
- 背题,当你抄题达到一定量后,可以去关注解题时间,刷题时尽量控制下时间,
自己给自己设置时间限制,不要让自己一直思考下去,如果遇到一个题目 40 分钟还没有想出来解题思路,建议先放弃。等到后面熟悉了,大脑形成记忆了再去解题。就好比乘法口诀表,熟悉之后才能运用到各个场景不是嘛; - 规范性,一段优秀的代码一定是规范的,所以从头开始养成一个良好习惯,有些人虽然解题快,但不规范的代码编写会在以后工作中造成很多麻烦,并且这样也不优雅,作为程序员我们应该时刻保持一个规范且优雅的姿态,做到保质又保量;
有很多题存在固定的通用的模版,背下模版可以节省大量时间,例如:双指针,BFS,DFS等等;- 不注重题量,重方法,保质不要量,不用非刷到 100 / 300 道题或者 1000 题才能找到工作。有些人可能刷到 300 道就悟了,有些人可能刷到 1000 题才开始有了思考的能力。有些同学浪费了快 1 年,刷了五百多题才得出这个结论。大多数同学没有思路直接看题解和代码,单纯默写,不去理解,就无法有突破。脑中没有思路的话可以先看题解中的解题思路,尽量通过代码实现。如果实在不行再看代码;
- 刷题的量其实是在锻炼你解题的思维逻辑,所以希望刚进入力扣刷题的小伙伴,能对每道题都有一个思考的过程,不管你的思考方向是否正确,至少扩展了;
- 建议先把官网「学习」单元里的每个基础数据结构、链表、二叉树、哈希表这些知识点理解透彻,且学会基础题目的解法,再去尝试初级题单;
- 如果看了题目没有解题思路,可以先去题解区上面搜索关键词或者观察别人题解的标题,要是这样再过几分钟想不出来的话可以仔细的做阅读笔记,随时复盘思考。对于大多数刷力扣题的同学来说,不管你以后从事的是哪个部门的职位,只要你是程序员,算法的功底可能就是你在众多选手中出挑的唯一法宝,也是大厂重要的敲门砖;
- 三思而后行,勤思考,实在想不出来再去看题解。勤写笔记,把自己的思路记在笔记中。举一反三,温故而知新,经常性的复习之前的题,加深印象,总结规律。
为什么见到一个题没思路?
- 这种情况大概率是因为见少了,刷题也是个缓慢的过程,见得多刷的多些,来的感觉才能更快一些。还有一部分可能因为给自己安排的刷题路线不够平和。你上来去肝hard难度的没思路是很正常的;
简单题很容易懂实现起来很难?
- 这种情况可能是由于基础逻辑缺乏训练导致的,对编程语言的集合框架掌握也有所欠缺。有些题可能涉及到集合框架(Map、Set、List、Stack、Queue),各种嵌套、联立需要你有个清晰的层次感和逻辑。刷题时,需要熟练使用一门编程语言,熟悉这个编程语言的常见操作API、集合框架、函数,这些是解决问题的工具帮助我们提高效率(不至于每次手写个队列、手写个哈希表吧)。这个问题推荐可以先刷几道简单的字符串处理问题,字符串处理问题很多涉及到的集合框架和逻辑控制比较多。
看了很多题解为啥还是不会刷题?
- 看了很多题没刷那跟没刷区别不太大,印象微弱。从学习角度,刷题和我们学数学的方式有点相似,学会了数学题公式和例题,但还需要大量练习才能真正掌握。只有自己亲身敲了每一行代码,每一行代码逻辑是什么,是自己思考出来的而不是看懂别人的思考。从 0 到 1 完整实现整个程序,这才能形成一个完整逻辑,然后可能出现各种bug自己调试看看找出问题。
可以看题解,看了自己要能完全写出来才行,如果刷了1000+题,你看了题解不刷没问题,看个思路过了被卡的地方就行。但如果刷了 100 不到,那你看懂题解后还是老老实实按照别人的逻辑闭卷式的复现一遍。
拿到一道题的处理流程:
- 确定考察点、确定思路:读到一个题,读完题意后首先就是要了解这个题到底考察的内容是什么?
首先可以确定下题型大类型,是图论?二叉树?字符串?然后要拿这个类型的题目往这个范畴常见算法上靠。比如给个数组数据让你查找计算,有可能是双指针,有可能是哈希,有可能还是位运算,还可能是动态规划,还可能是要贪心处理。不过大部分题是在各个经典算法的经典问题上进行一些变化,要知道经典算法处理了哪些经典问题。如果能确定考察点,可以想想细节开始实现;如果确定不了考察点,没思路,先别直接看题解,看看题目"标签"的提示。有时你看一个题可能说:这题啥方法啊我只会暴搜,有的确实就是搜索剪枝; 除了标签,还要看"数据范围"!数据范围内的数据都是可能出现的,不同数据范围可能使用方法不同(这点数组题较多,有些题巧用哈希、原地置换对数据有要求)。如果自己看了标签想想来灵感那最好,如果还是没有灵感,那点一下题解。可以从题解标题中看看能不能有灵感,有不少题解会给足够多的暗示有些人看到就能明白了。如果还是不会那就老老实实点进去看看别人的思路,有的是视频,有的是图文,看懂为止,要是还自己看不懂,那就请教一下别人吧!有的算法题逻辑想不明白,把代码加断点,加输出打印,一步一步走,用笔用纸,一步一步画,最好用铅笔橡皮,实在想不通的地方,就先pass掉,把被卡住的地方记录下来,去问更厉害的人,不要在一道题上卡太长时间,一道题的时间大概为40分钟;
编写代码、测试:
编写代码的过程不要有任何参考!编写代码的过程不要有任何参考!重要的话说两遍,思路可以看,别人的代码也可以看,你自己写代码不要参考和 ctrl c + ctrl v,工程项目能跑起来就行,为了效率都是 cv 大法,但是面试笔试题基本要你闭卷,有的还要你用在线IDE连提示都不全的;- 写代码常常要考虑常见问题:测试数据边界(比如Integer.MAX_VALUE,Integer.MIN_VALUE这种边界数值),循环控制边界处理,末尾数据处理(有时候会被遗忘处理),特殊异常情况考虑,数值范围是否合理,算法复杂度是否能够跑出来,数据深浅拷贝,简化重复遍历和操作,变量命名清晰,注释较为完整等等;
- 写完代码,用测试案例多测测,确保万无一失。力扣经常出空值测试案例,因为这个wa了很多次;
- 如果出现和想象中不一样的问题,先看一遍自己代码逻辑看看能否看出问题,如果看得出正好,看不出的话自己打印输出或者debug找找问题,直到改对为止,有很多题需要考虑比较全才能ac;
方法、结果对比:
不要以为ac了就OK了,你要看看自己时间上超越了多少人,推荐从这两个维度来衡量自己的代码:要超越70%以上的人(根据自己要求适当提高):大部分题超越70%说明你的方法上是没问题的,可能有些小的方面可以进行优化。比如StringBuilder替代String进行字符串拼接,使用char[]数组替代String进行遍历枚举等等;- 自己的方法在好方法时间范围内:有些题比较卷,大家都是最快方法,你的代码可能比别人差1ms就显得很慢,这时你只要确定你的方法很优秀就可以不一定要追求100%,并且这个时间花销不同评测机器出来结果可能也不同的。可以看看大家的时间花销区间,如果你的方法跟最快的在几 ms 或者 30%时间范围,其实都是ok的。别人4ms,你5ms没啥问题,别人50ms,你 70ms也没啥问题,但是如果别人80ms,你800ms那差的太多就要看看自己逻辑和代码了;
- 另外,力扣你点击前面时间的柱状图是可以看到别人时间开销较小的代码(有的现在跑可能因为测试数据变动没那么快了),可以参考学习一下别人的处理方式;
巩固提高:
- 过了这道题,可以看看题解区,别人有没有更巧妙的处理方法,当你自己ac之后和别人有个直接对比,印象会比较深刻:还可以这样!
- 力扣上hard题一般逻辑量大或者难,easy和mid可能简单,但有些题目后面反问你能用 O(1),O(n) 等等限制条件解决的还是很需要技巧性的,有必要掌握!如果感觉这类题型掌握不扎实还想再练一下可以看相似题型去及时巩固一下;
- 上面的一些方法仅限于给一些初学者建议,可以参考。如果上面题差不多有闲余之力,推荐可以 跟着力扣每日一题打卡,半年就是180+题量,一年就是365题量,相当可观,方法和路线不是最难的,最难的是坚持,希望和大家一起在后面的路上不变秃但是变强;
其中,暴力枚举、贪心算法容易理解,可以很快上手。
数论相关的算法需要用到一些数学技巧,
包括位运算、幂函数、求模等等性质。
二分算法和深度优先搜索算法相对有些技巧性,好在他们都有固定的模板。
另外,不得不提的是,[深度优先搜索算法]的思想非常重要,
而且深度优先搜索是动态规划、分治和回溯的基础,需要重点掌握。
刷题套路
先快速识别出题干的主要数据结构,再相应对策略。
综合:
- 求利润时,记得代码中要出现2个数相减;
- 每道题可能有多个解法,不用尝试把所有解法都写一遍,但如果你的写法的时间复杂度或空间复杂度比较高,那就要尝试换一种写法了;
如果求[最小值/最大值],先为这个值创建变量,再通过[Math.max()/Max.min()]来解决问题,可用于数组,树
遍历:
- 允许while嵌套,在小while里可以一直循环查树的左子节点,直到左子节点为null为止;
递归:
- 当给的模版方法不适合做递归时,可以新建个适合做递归的方法,然后将这个方法被模版方法调用;
数组:
- 如果参数是默认有序的,则可以使用[双指针遍历]来快速查找元素;
- 如果元素值与下标相同,或存在某些关系,则两者可以互换,例如:int a = {1, 2, 3}; a.length = 3, a[1] = 1,a[2] = 2,a[3] = 3;
链表:
- 在某些场合,不要拿参数的链表直接改,因为原来的列表里是有一堆next引用的,容易改出环,在遍历时可以将current.next转存给一个新变量,再去改current.next,新变量还是原来的值;
哈希表:
反复检查某个容器中是否存在某个值需要使用HashSet,需要O(1)的时间,而对于其他数据结构,则需要O(n)的时间。选择正确的数据结构是解决这些问题的关键部分;
树:
- 一条路径的长度为该路径经过的节点数减一;
高频算法模版
其实你可以把它们背下来的。
双指针
双指针是一种常见的算法技巧,在处理[数组/链表]问题时特别有用,
使用双指针技巧可以大大降低时间复杂度。
特点:
- 双指针排序法并不一定非要左右开弓,也有可能是2边同时从一侧开始起步,只不过增速有快有慢;
- 双指针还有个变体,快慢指针,龟兔赛跑,用于链表中的是否有环,求2个链表的相同部分等等;
一些常见的使用场景包括:
- 查找[数组/链表]中是否存在某个特定元素或子序列,或其起始位置和结束位置;
- 判断是否回文,回文字符串(回文串是指正着读和倒着读都一样的字符串,例如:level),回文数组,回文链表。确定数组是否回文很简单,我们可以使用双指针法来比较两端的元素,并向中间移动。一个指针从起点向中间移动,另一个指针从终点向中间移动;
- 在一个已排序的[数组/链表]中查找满足某种条件的元素;
需要注意的是,使用双指针并不一定能解决所有问题,
有时可能需要结合其他算法技巧进行处理。
只有一个输入, 从两端开始遍历:
public int fn(int[] arr) { int left = 0; int right = arr.length - 1; int ans = 0; while (left < right) { // 一些根据 letf 和 right 相关的代码补充 if (CONDITION) { left++; } else { right--; } } return ans; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
有两个输入, 两个都需要遍历完:
public int fn(int[] arr1, int[] arr2) { int i = 0, j = 0, ans = 0; while (i < arr1.length && j < arr2.length) { // 根据题意补充代码 if (CONDITION) { i++; } else { j++; } } while (i < arr1.length) { // 根据题意补充代码 i++; } while (j < arr2.length) { // 根据题意补充代码 j++; } return ans; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
二分查找
普通:
public int fn(int[] arr, int target) { int left = 0; int right = arr.length - 1; while (left <= right) { int mid = left + (right - left) / 2; if (arr[mid] == target) { // 根据题意补充代码 return mid; } if (arr[mid] > target) { right = mid - 1; } else { left = mid + 1; } } // left 是插入点 return left; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
广度优先搜索
对树的每一层进行操作,主要用队列的size来遍历属于相同层的节点。
二叉树:
public int fn(TreeNode root) { Queue<TreeNode> queue = new LinkedList<>(); queue.add(root); int ans = 0; while (!queue.isEmpty()) { int currentLength = queue.size(); // 做一些当前层的操作 for (int i = 0; i < currentLength; i++) { TreeNode node = queue.remove(); // 根据题意补充代码 if (node.left != null) { queue.add(node.left); } if (node.right != null) { queue.add(node.right); } } } return ans; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
深度优先搜索
二叉树(迭代):
public int dfs(TreeNode root) { Stack<TreeNode> stack = new Stack<>(); stack.push(root); int ans = 0; while (!stack.empty()) { TreeNode node = stack.pop(); // 根据题意补充代码 if (node.left != null) { stack.push(node.left); } if (node.right != null) { stack.push(node.right); } } return ans; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
二叉树(递归):
public int dfs(TreeNode root) {
if (root == null) {
return 0;
}
int ans = 0;
// 根据题意补充代码
dfs(root.left);
dfs(root.right);
return ans;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
[二叉搜索树/二叉排序树/二叉查找树]模板
如果题干中出现二叉搜索树,那我们可以快速得知一些套路,
我们可以快速地找出树中的某个节点以及从根节点到该节点的路径,
假设我们需要找到节点x,我们从根节点开始遍历,
如果当前节点就是x,那么成功地找到了节点。
如果当前节点的值大于x的值,说明x应该在当前节点的左子树,
因此将当前节点移动到它的左子节点。
如果当前节点的值小于x的值,说明x应该在当前节点的右子树,
因此将当前节点移动到它的右子节点。
在寻找节点的过程中,我们可以顺便记录经过的节点,
这样就得到了从根节点到被寻找节点的路径。
public List<TreeNode> getPath(TreeNode root, TreeNode target) {
List<TreeNode> path = new ArrayList<TreeNode>();
TreeNode node = root;
while (node != target) {
path.add(node);
if (target.val < node.val) {
node = node.left;
} else {
node = node.right;
}
}
path.add(node);
return path;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
动态规划模板
- 可以用递归,也可以不用递归,如果不用递归的话,则需要使用for,去循环动态移动;



