这是一个简单的贝叶斯网络结构图的示例。图中包含三个节点：“Rain”（下雨）、“Sprinkler”（洒水器）和“Grass Wet”（草地湿润）。节点之间的有向边表示变量之间的因果关系，例如“Rain”和“Sprinkler”都直接影响“Grass Wet”。这种图形化的表示有助于理解变量之间的概率依赖关系。

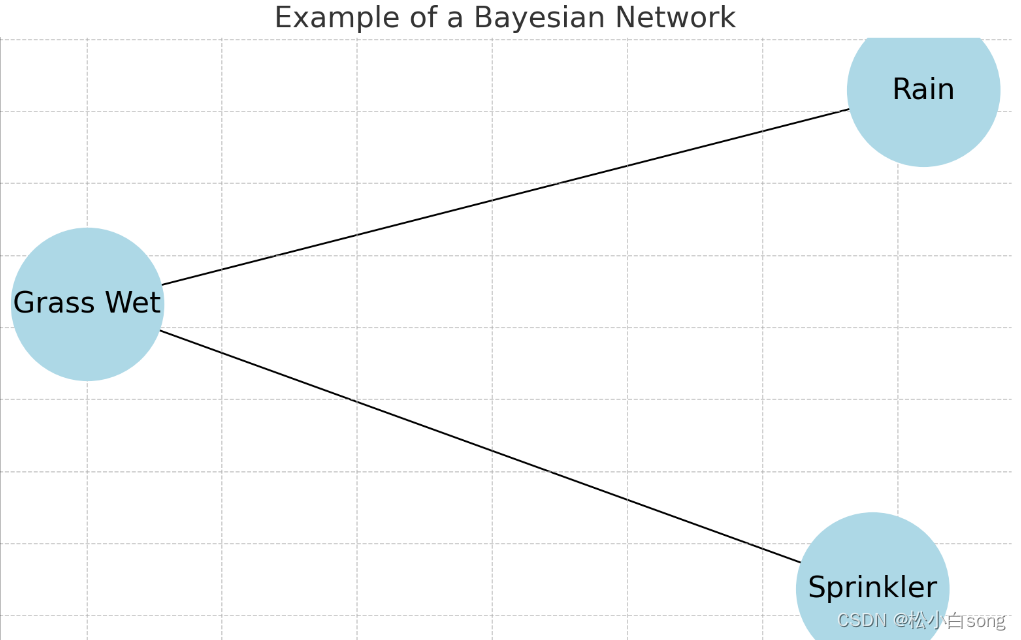
1.2概率模型

在贝叶斯网络中，每个节点都有一个与之相关的条件概率表（Conditional Probability Table, CPT），该表描述了在给定父节点状态下该节点状态的概率分布。这使得贝叶斯网络能够通过链式规则来计算整个网络的联合概率分布。

1.3应用场景

贝叶斯网络被广泛应用于多种领域，包括：

医疗诊断：结合病人的各种症状和已知的病因关系，预测病人可能患有的疾病。
机器学习：用于分类、预测和异常检测等。
风险管理：在金融和保险领域评估和管理风险。
自然语言处理：用于词义消歧、句法分析等。

1.4推理方法

贝叶斯网络的一个核心功能是推理，即根据已知的部分信息来推测未知变量的状态。推理通常分为两类：

准确推理：通过数学严格计算得到精确结果，例如使用联合概率分布表或变量消元技术。
近似推理：在计算复杂或数据量庞大时使用，如采样方法（蒙特卡洛方法）和变分推理方法。

1.5学习

贝叶斯网络的学习可以分为结构学习和参数学习：

结构学习：从数据中学习节点之间的依赖关系（即网络结构）。
参数学习：确定条件概率表中的参数，通常通过最大似然估计或贝叶斯估计来实现。

二、贝叶斯网络在机器学习中的应用

贝叶斯网络在机器学习中的应用十分广泛，它能够提供强大的框架来处理具有不确定性和复杂依赖关系的数据。以下是一些贝叶斯网络在机器学习中的主要应用：

分类问题：贝叶斯网络被用于分类任务，特别是在特征之间存在复杂的条件依赖时。通过网络，可以利用已知的特征来预测未知类别标签的概率。例如，垃圾邮件过滤器可以使用贝叶斯网络来判断一封邮件是否为垃圾邮件。

预测建模：在金融、销售、气象等领域，贝叶斯网络可以预测未来的趋势和事件。例如，通过分析历史数据中的经济指标，贝叶斯网络可以用来预测股市的走向。

推荐系统：贝叶斯网络可以应用于推荐系统中，通过分析用户的历史行为和偏好，预测用户可能感兴趣的新产品或服务。例如，一个视频流服务可以使用贝叶斯网络来推荐用户可能喜欢的电影或电视节目。

异常检测：在网络安全和工业生产中，贝叶斯网络可以用来检测行为或数据中的异常模式。例如，一个网络安全系统可能使用贝叶斯网络来识别不寻常的登录尝试或数据传输，这可能表明安全威胁。

自然语言处理：贝叶斯网络在自然语言处理中的应用包括词义消歧、情感分析和机器翻译。它们能够考虑上下文中的词语依赖性，改进语言模型的准确性。

结构化学习和知识发现：在生物信息学和医学研究中，贝叶斯网络可以用来发现变量之间的潜在关系，如基因表达数据中的调控网络。此外，它还可以用于识别疾病与遗传因素之间的复杂关系。

强化学习：在强化学习中，贝叶斯网络可以用来建模和优化决策过程，特别是在环境模型不完全已知的情况下。它们可以用来估计状态转移概率和奖励函数。

三、应用实例

3.1分类

这段代码首先定义了一个贝叶斯网络，包括节点和边，以及每个节点的条件概率表。然后，我们使用 pgmpy 的推理工具来查询在给定智力高和课程困难的情况下，学生的各个成绩等级的概率。这可以帮助我们理解如何在实际应用中使用贝叶斯网络进行决策和预测。

代码：


from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
 
# 定义模型结构
model = BayesianNetwork([('Difficulty', 'Grade'), ('Intelligence', 'Grade')])
 
# 定义条件概率分布
cpd_difficulty = TabularCPD(variable='Difficulty', variable_card=2, values=[[0.6], [0.4]])
cpd_intelligence = TabularCPD(variable='Intelligence', variable_card=2, values=[[0.7], [0.3]])
 
# Grade 取决于 Difficulty 和 Intelligence
cpd_grade = TabularCPD(variable='Grade', variable_card=3,
                       values=[[0.3, 0.05, 0.9, 0.5],   # P(Grade=0|Difficulty, Intelligence)
                               [0.4, 0.25, 0.08, 0.3],  # P(Grade=1|Difficulty, Intelligence)
                               [0.3, 0.7, 0.02, 0.2]],  # P(Grade=2|Difficulty, Intelligence)
                       evidence=['Difficulty', 'Intelligence'],
                       evidence_card=[2, 2])
 
# 将条件概率分布添加到模型中
model.add_cpds(cpd_difficulty, cpd_intelligence, cpd_grade)
 
# 验证模型的一致性
assert model.check_model()
 
# 使用变量消除进行推理
inference = VariableElimination(model)
 
# 查询一个学生在智力高、课程困难的情况下及格的概率
result = inference.query(variables=['Grade'], evidence={'Intelligence': 1, 'Difficulty': 1})
print(result)

结果：

3.2推荐系统

这段代码创建了一个包含三个变量（年龄、电影类型、评分）的贝叶斯网络，并为每个变量定义了条件概率分布。我们使用变量消除方法来预测不同年龄段和电影类型的用户对电影的喜好。这样的系统可以帮助推荐系统更精确地预测用户的喜好，进而推荐更合适的电影。

代码：


from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
 
# 定义模型结构
model = BayesianNetwork([('Age', 'Rating'), ('Genre', 'Rating')])
 
# 定义条件概率分布
# Age: 0 = Young, 1 = Adult, 2 = Elderly
cpd_age = TabularCPD(variable='Age', variable_card=3, values=[[0.3], [0.5], [0.2]])
 
# Genre: 0 = Action, 1 = Romance
cpd_genre = TabularCPD(variable='Genre', variable_card=2, values=[[0.6], [0.4]])
 
# Rating: 0 = Dislike, 1 = Like
cpd_rating = TabularCPD(variable='Rating', variable_card=2,
                        values=[[0.5, 0.2, 0.9, 0.1, 0.6, 0.3],  # P(Rating=Dislike|Age,Genre)
                                [0.5, 0.8, 0.1, 0.9, 0.4, 0.7]], # P(Rating=Like|Age,Genre)
                        evidence=['Age', 'Genre'],
                        evidence_card=[3, 2])
 
# 将条件概率分布添加到模型中
model.add_cpds(cpd_age, cpd_genre, cpd_rating)
 
# 验证模型的一致性
assert model.check_model()
 
# 使用变量消除进行推理
inference = VariableElimination(model)
 
# 查询不同年龄段和电影类型下用户喜欢电影的概率
result_young_action = inference.query(variables=['Rating'], evidence={'Age': 0, 'Genre': 0})
result_adult_romance = inference.query(variables=['Rating'], evidence={'Age': 1, 'Genre': 1})
print("Young and Action Movie Rating:\n", result_young_action)
print("Adult and Romance Movie Rating:\n", result_adult_romance)

结果：

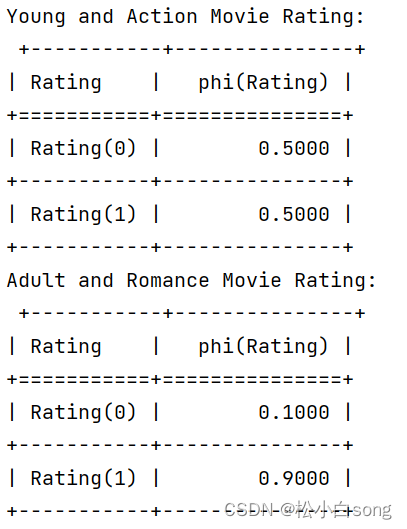
3.3自然语言处理

这段代码构建了一个贝叶斯网络，模拟了关键词和主题对文本情感的影响。通过条件概率表（CPD）定义了每个变量间的关系，并通过变量消除方法进行情感预测。

代码：


from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
 
# 定义模型结构
model = BayesianNetwork([('Keywords', 'Sentiment'), ('Topic', 'Sentiment')])
 
# 定义条件概率分布
# Keywords: 0 = Positive, 1 = Negative
cpd_keywords = TabularCPD(variable='Keywords', variable_card=2, values=[[0.7], [0.3]])
 
# Topic: 0 = Technology, 1 = Economy
cpd_topic = TabularCPD(variable='Topic', variable_card=2, values=[[0.6], [0.4]])
 
# Sentiment: 0 = Positive, 1 = Negative
cpd_sentiment = TabularCPD(variable='Sentiment', variable_card=2,
                           values=[[0.9, 0.6, 0.7, 0.2],  # P(Sentiment=Positive|Keywords,Topic)
                                   [0.1, 0.4, 0.3, 0.8]], # P(Sentiment=Negative|Keywords,Topic)
                           evidence=['Keywords', 'Topic'],
                           evidence_card=[2, 2])
 
# 将条件概率分布添加到模型中
model.add_cpds(cpd_keywords, cpd_topic, cpd_sentiment)
 
# 验证模型的一致性
assert model.check_model()
 
# 使用变量消除进行推理
inference = VariableElimination(model)
 
# 查询在特定关键词和主题下的情感概率
result = inference.query(variables=['Sentiment'], evidence={'Keywords': 0, 'Topic': 0})
print(result)

结果：

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家自动化/article/detail/674944