机器学习——随机森林原理及Python实现_随机森林交叉验证

一、理论

1.随机森林介绍

从直观角度来解释，每棵决策树都是一个分类器（假设现在针对的是分类问题），那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的 Bagging 思想。

1.1 随机森林中“树”的生成

每棵树的按照如下规则生成：

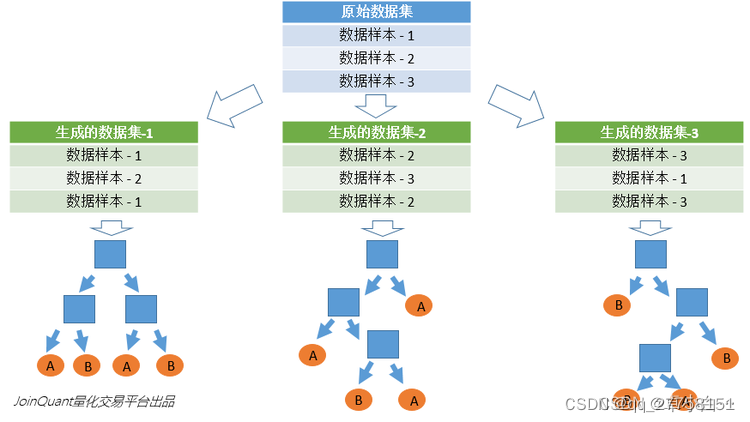
1.一个样本容量为N的样本，有放回的抽取N次，每次抽取1个，最终形成了N个样本。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。
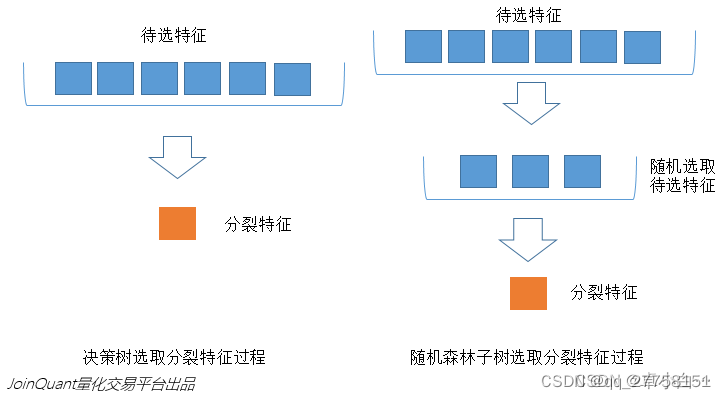
2.当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
3.决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了），一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
4.按照步骤1~3建立大量的决策树，这样就构成了随机森林了。
这里有两个问题：

Problem1 ： 为什么要随机抽样训练集？
如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的，这样的话完全没有bagging的必要；

Problem2： 为什么要有放回地抽样？

如果不放回抽样，每棵树用的样本完全不同，结果是有偏的，基学习器之间的相似性小，投票结果差，模型偏差大
如果不抽样，基学习器用所有样本，那么模型的泛化能力弱，基学习器之前相似性太大差异性太小，模型的偏差大

2、Random Forest 优缺点

2.1 .优点

它可以出来很高维度（特征很多）的数据，并且不用降维，无需做特征选择
不容易过度拟合
对于不平衡的数据集来说，它可以平衡误差。
如果有很大一部分的特征遗失，仍可以维持准确度。

2.2 .缺点

随机森林已经被证明在某些噪音较大的分类或回归问题上会过度拟合
由于随机林使用许多决策树，因此在较大的项目上可能需要大量内存。这可以使它比其他一些更有效的算法慢

3. 随机森林分类效果（错误率）的影响因素：

随机森林分类效果（错误率）与两个因素有关：

森林中任意两棵树的相关性：相关性越大，错误率越大；
森林中每棵树的分类能力：每棵树的分类能力越强，整个森林的错误率越低。
减小特征选择个数m，树的相关性和分类能力也会相应的降低；增大m，两者也会随之增大。所以关键问题是如何选择最优的m（或者是范围），这也是随机森林唯一的一个参数。

4 袋外错误率（oob error）

上面我们提到，构建随机森林的关键问题就是如何选择最优的m，要解决这个问题主要依据计算袋外错误率oob error（out-of-bag error）。

随机森林有一个重要的优点就是，没有必要对它进行交叉验证或者用一个独立的测试集来获得误差的一个无偏估计。它可以在内部进行评估，也就是说在生成的过程中就可以对误差建立一个无偏估计。

在构建每棵树时，我们对训练集使用了不同的bootstrap sample（随机且有放回地抽取）。所以对于每棵树而言（假设对于第k棵树），大约有1/3的训练实例没有参与第k棵树的生成，它们称为第k棵树的oob样本。

而这样的采样特点就允许我们进行oob估计，它的计算方式如下：

（note：以样本为单位）

1）对每个样本，计算它作为oob样本的树对它的分类情况（约1/3的树）；

2）然后以简单多数投票作为该样本的分类结果；

3）最后用误分个数占样本总数的比率作为随机森林的oob误分率。

二、实战

1.代码实现流程：

2.库

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score

3.类

RandomForestClassifier(n_estimators=100, *, criterion=‘gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=‘auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None, ccp_alpha=0.0, max_samples=None)

3.1参数：

• n_estimators=100, *, # 树的棵树，默认是100
• criterion=‘mse’, # 默认“ mse”，衡量质量的功能，可选择“mae”。
• max_depth=None, # 树的最大深度。
  min_samples_split=2, # 拆分内部节点所需的最少样本数：
• min_samples_leaf=1, # 在叶节点处需要的最小样本数。
• min_weight_fraction_leaf=0.0, # 在所有叶节点处的权重总和中的最小加权分数。
• max_features=‘auto’, # 寻找最佳分割时要考虑的特征数量。
• max_leaf_nodes=None, # 以最佳优先方式生长具有max_leaf_nodes的树。
• min_impurity_decrease=0.0, # 如果节点分裂会导致杂质的减少大于或等于该值，则该节点将被分裂。
• min_impurity_split=None, # 提前停止树木生长的阈值。
• bootstrap=True, # 建立树木时是否使用bootstrap抽样。 如果为False，则将整个数据集用于构建每棵决策树。
• oob_score=False, # 是否使用out-of-bag样本估算未过滤的数据的R2。
• n_jobs=None, # 并行运行的Job数目。
• random_state=None, # 控制构建树时样本的随机抽样
• verbose=0, # 在拟合和预测时控制详细程度。
• warm_start=False, # 设置为True时，重复使用上一个解决方案，否则，只需拟合一个全新的森林。
• ccp_alpha=0.0,
• max_samples=None # 如果bootstrap为True，则从X抽取以训练每个决策树。

4.代码

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import  GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_auc_score

##step1.读取数据
wine=pd.read_csv('data/wine/wine.csv')
# 简单数据信息查看
# wine.info()
# print(wine.head(3))
# print(wine.describe())
#id列和label列是int，其他都是float,11个特征，1个label
# 数据处理,构造特征集和标签集
x = wine.iloc[:,0:12]#取不带标签的数据
y = wine.iloc[:,12]#标签值
y[y<=6] = 0
y[y>6] =1
# 划分训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=16,test_size=0.3)
# 实例化
rfc=RandomForestClassifier()
# 训练
rfc.fit(x_train,y_train)
# 预测
ypred=rfc.predict(x_test)
# print(ypred)
# 模型评估
#score
score1=rfc.score(x_test,y_test)
print(score1)
#
# proba=rfc.predict_proba(x_test)#使用分类器预测测试集中每个样本属于0和1的概率
# # print(proba)
# #roc
# score2=roc_auc_score(y_test,ypred)
# print(score2)
# # cross交叉验证得分
# score3=cross_val_score(rfc,x_train,y_train,scoring='accuracy',cv=3)#scoring='accuracy'表示评分标准是准确率，cv = 3表示交叉验证的折数为3折
# print(score3.mean())#整体平均得分
# 特征重要性
# importance=rfc.feature_importances_
# col=np.array(x.columns)
# re=pd.DataFrame({'特征名':col,'特征重要性':importance}).sort_values(by='特征重要性',axis=0,ascending=False)
# print(re)
# 调参
# n_estimators
# 树的棵数，50-300，步长50
# GridSearchCV网格搜索:
# estimator:选择使用的分类器,param_grid:需要最优化的参数的取值, scoring:模型评价标准
num_estimator={'n_estimators':range(50,300,50)}
gs1=GridSearchCV(estimator=rfc,param_grid=num_estimator,scoring='roc_auc',cv=3)
gs1.fit(x_train,y_train)
print('best_n_estimators',gs1.best_estimator_)#RandomForestClassifier(n_estimators=200)
print(gs1.best_score_)
# n_estimators=200,调整max_depth
maxdepth={'max_depth':range(3,10,1)}
gs2=GridSearchCV(estimator=RandomForestClassifier(n_estimators=200),param_grid=maxdepth,scoring='roc_auc',cv=3)
gs2.fit(x_train,y_train)
print('best_max_depth',gs2.best_estimator_)#best_max_depth RandomForestClassifier(max_depth=9, n_estimators=200)
print(gs2.best_score_)#得分降了？



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66