热门标签
热门文章
- 1基于Flink CDC实时同步数据(MySQL到MySQL)_flink-sql-connector-mysql-cdc
- 2k8s创建pv&pvc_k8s 创建pv
- 3力扣151--反转字符串中的单词(优)
- 4wwwwwwwwwwwww_26u
- 5vscode遇到无法访问此网站问题的两种解决方法_vscode官网无法访问
- 6【unity实践demo】unity之子弹发射_unity 旋转发射
- 7银河麒麟V10下载安装使用体验(上)_银河麒麟v10镜像iso下载
- 8移植conda环境到另一台服务器上_conda环境复制到另一台电脑
- 9vscode更新至1.86版本后,ssh远程连接服务器出现异常
- 10linux+nginx+tomcat+vue+后端项目部署_linux 在tomcat上部署java项目和vue项目
当前位置: article > 正文
第4章 学习Shader所需的数学基础(终)(Unity Shader内置变量与练习题答案)_unityshader入门练习题 4.2.5答案
作者:知新_RL | 2024-02-18 11:35:31
赞
踩
unityshader入门练习题 4.2.5答案
4.8 Unity Shader的内置变量(数学篇)
使用Unity 写Shader 的一个好处在于,它提供了很多内置的参数,这使得我们不再需要自己手动计算一些值。本节将给出Unity 内置的用于空间变换和摄像机以及屏幕参数的内置变量。这些内置变量可以在UnityShaderVariables.cginc 文件中找到定义和说明。
读者: 为什么在我的Unity 中,有些变量不存在呢?
我们:可能是由于你使用的Unity 版本和本书使用的版本不同。在写本书时,我们使用的Unity版本是最新的5.2 . 而在4.x 版本中, 一些内置变量可能会与之不同。
4.8.1 变换矩阵
首先是用于坐标空间变换的矩阵。表4.2 给出了Unity 5.2 版本提供的所有内置变换矩阵。下面所有的矩阵都是float4x4 类型的。读者: 为什么在我的Unity 中,有些变量不存在呢?
我们:可能是由于你使用的Unity 版本和本书使用的版本不同。在写本书时,我们使用的Unity版本是最新的5.2 . 而在4.x 版本中, 一些内置变量可能会与之不同。

表4.2 给出了这些矩阵的常见用法。但读者可以根据需求来达到不同的目的,例如我们可以提取坐标空间的坐标轴,方法可回顾4.6.2 节。
其中有一个矩阵比较特殊,即UNITY_MATRIX_T_MV 矩阵。很多对数学不了解的读者不理解这个矩阵有什么用处。如果读者认真看过矩阵一节的知识,应该还会记得一种非常吸引人的矩阵类型一一正交矩阵。对于正交矩阵来说,它的逆矩阵就是转置矩阵。因此,如果UNITY_MATRIX_MV 是一个正交矩阵的话,那么UNITY_MATRIX_T_MV 就是它的逆矩阵,也就是说,我们可以使用UNITY_MATRIX_T_MV 把顶点和方向矢量从观察空间变换到模型空间。
那么问题是, UNITY_MATRIX_MV 什么时候是一个正交矩阵呢?读者可以从4.5 节找到答案。总结一下,如果我们只考虑旋转、平移和缩放这3 种变换的话,如果一个模型的变换只包括旋转,那么UNITY_MATRIX_MV 就是一个正交矩阵。这个条件似乎有些苛刻,我们可以把条件再放宽一些,如果只包括旋转和统一缩放〈假设缩放系数是k) ,那么UNITY_MATRIX_MV 就几乎是一个正交矩阵了。为什么是几乎呢?因为统一缩放可能会导致每一行(或每一列)的矢量长度不为1 ,而是k,这不符合正交矩阵的特性,但我们可以通过除以这个统一缩放系数,来把它变成正交矩阵。在这种情况下,UNITY_MATRIX_MV 的逆矩阵就是
其中有一个矩阵比较特殊,即UNITY_MATRIX_T_MV 矩阵。很多对数学不了解的读者不理解这个矩阵有什么用处。如果读者认真看过矩阵一节的知识,应该还会记得一种非常吸引人的矩阵类型一一正交矩阵。对于正交矩阵来说,它的逆矩阵就是转置矩阵。因此,如果UNITY_MATRIX_MV 是一个正交矩阵的话,那么UNITY_MATRIX_T_MV 就是它的逆矩阵,也就是说,我们可以使用UNITY_MATRIX_T_MV 把顶点和方向矢量从观察空间变换到模型空间。
那么问题是, UNITY_MATRIX_MV 什么时候是一个正交矩阵呢?读者可以从4.5 节找到答案。总结一下,如果我们只考虑旋转、平移和缩放这3 种变换的话,如果一个模型的变换只包括旋转,那么UNITY_MATRIX_MV 就是一个正交矩阵。这个条件似乎有些苛刻,我们可以把条件再放宽一些,如果只包括旋转和统一缩放〈假设缩放系数是k) ,那么UNITY_MATRIX_MV 就几乎是一个正交矩阵了。为什么是几乎呢?因为统一缩放可能会导致每一行(或每一列)的矢量长度不为1 ,而是k,这不符合正交矩阵的特性,但我们可以通过除以这个统一缩放系数,来把它变成正交矩阵。在这种情况下,UNITY_MATRIX_MV 的逆矩阵就是
1/k UNITY_MATRIX_T_MV。 而且,如果我们只是对方向矢量进行变换的话,条件可以放得更宽,即不用考虑有没有平移变换,因为平移对方向矢量没有影响。因此,我们可以截取UNITY_MATRIX_T_MV 的前3 行前3 列来把方向矢量从观察空间变换到模型空间〈前提是只存在旋转变换和统一缩放〉。对于方向矢量,我们可以在使用前对它们进行归一化处理,来消除统一缩放的影响。
还有一个矩阵需要说明一下,那就是UNITY_MATRIX_IT_MY 矩阵。我们在4.7 节已经知道,法线的变换需要使用原变换矩阵的逆转置矩阵。因此UNITY_MATRIX_IT_MV 可以把法线从模型空间变换到观察空间。但只要我们做一点手脚,它也可以用于直接得到UNITY_MATRIX_MV 的逆矩阵一一我们只需要对它进行转置就可以了。因此,为了把顶点或方向矢量从观察空间变换到模型空间,我们可以使用类似下面的代码:
还有一个矩阵需要说明一下,那就是UNITY_MATRIX_IT_MY 矩阵。我们在4.7 节已经知道,法线的变换需要使用原变换矩阵的逆转置矩阵。因此UNITY_MATRIX_IT_MV 可以把法线从模型空间变换到观察空间。但只要我们做一点手脚,它也可以用于直接得到UNITY_MATRIX_MV 的逆矩阵一一我们只需要对它进行转置就可以了。因此,为了把顶点或方向矢量从观察空间变换到模型空间,我们可以使用类似下面的代码:
- // 方法一, 使用transpose 函数对UNITY_MATRIX_IT_MV 进行转置,
- // 得到UNITY_MATRIX_MV 的逆矩阵,然后进行列矩阵乘法,
- // 把观察空间中的点或方向矢量变换到模型空间中
- float4 modelPos = mul(transpose(UNITY_MATRIX_ IT_MV), viewPos);
-
- // 方法二, 不直接使用转置函数transpose ,而是交换mul 参数的位置,使用行矩阵乘法
- // 本质和方法一是完全一样的
- float4 modelPos = mul(viewPos, UNITY_MATRIX_IT_MV);
4.8.2 摄像机和屏幕参数
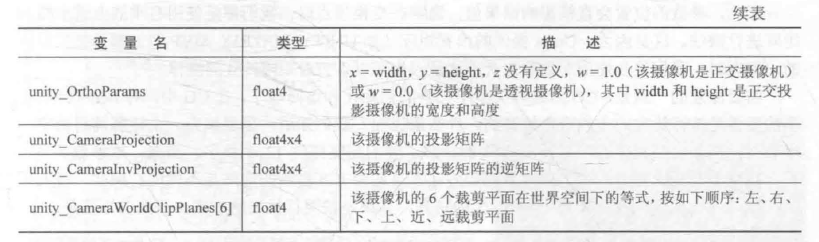
Unity 提供了一些内置变量来让我们访问当前正在渲染的摄像机的参数信息。这些参数对应了摄像机上的Camera 组件中的属性值。表4.3 给出了Unity 5.2 版本提供的这些变量。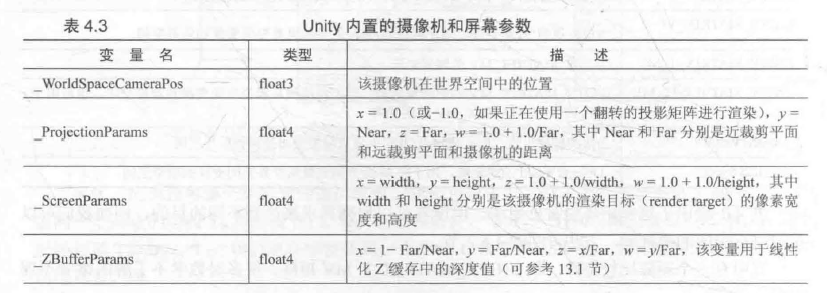
4.9 答疑解惑
恭喜你已经几乎完成了本书所有的数学训练!我们希望你能从上面的内容中得到很多收获和启发。但是,我们也相信在读完上面的内容后你可能对某些概念仍然感到迷惑。不要担心,答疑解惑一节就可以帮你跨过一些障碍。
4.9.1 使用3x3 还是4x4 的变换矩阵
对于线性变换(例如旋转和缩放)来说,仅使用3×3 的矩阵就足够表示所有的变换了。但如果存在平移变换,我们就需要使用4×4 的矩阵。因此,在对顶点的变换中,我们通常使用4x4 的变换矩阵。当然,在变换前我们需要把点坐标转换成齐次坐标的表示,即把顶点的w 分量设为1。而在对方向矢量的变换中,我们通常使用3x3的矩阵就足够了,这是因为平移变换对方向矢量是没有影响的。4.9.2 CG 中的矢量和矩阵类型
我们通常在Unity Shader 中使用CG 作为着色器编程语言。在CG 中变量类型有很多种,但在本节我们是想解释如何使用这些类型进行数学运算。因此,我们只以float 家族的变量来做说明。在CG 中, 矩阵类型是由float3x3 、float4x4 等关键词进行声明和定义的。而对于float3 、float4等类型的变量,我们既可以把它当成一个矢量,也可以把它当成是一个1 x n 的行矩阵或者一个n x 1 的列矩阵。这取决于运算的种类和它们在运算中的位置。例如,当我们进行点积操作时,两个操作数就被当成矢量类型,如下:
- float4 a = float4(1.0, 2.0, 3.0 4.0);
- float4 b = float4(1.0, 2.0, 3.0,4.0);
- //对两个矢量进行点积操作
- float result= dot(a, b);
- float4 v = float4(1 O, 2.0, 3.0 , 4.0);
- float4x4 M = float4x4(1.0, 0.0, 0.0, 0.0 ,
- 0.0, 1.0, 0.0, 0.0,
- 0.0, 0.0, 1.0, 0.0,
- 0.0, 0.0, 0.0, 1.0);
- // 把v当成列矩阵和矩阵M 进行右乘
- float4 column_mul_result = mul(M, v);
- // 把v当成行矩阵和短阵M 进行左乘
- float4 row_mul_result = mul(v, M);
- // 注意· column_mul_result 不等于row_mul_result ,而是.
- // mul(M,v) == mul(v, tranpose(M))
- // mul(v,M) == mul(tranpose(M), v)
需要注意的一点是, CG 对矩阵类型中元素的初始化和访问顺序。在CG 中,对float4x4 等类型的变量是按行优先的方式进行填充的。什么意思呢?我们知道,想要填充一个矩阵需要给定一串数字,例如,如果需要声明一个3x3的矩阵,我们需要提供12 个数字。那么,这串数字是一行一行地填充矩阵还是一列一列地填充矩阵呢?这两种方式得到的矩阵是不同的。例如,我们使
用( 1, 2, 3, 4, 5, 6, 7, 8, 9)去填充一个3 × 3 的矩阵,如果是按照行优先的方式,得到的矩阵是:

CG 使用的是行优先的方法,即是一行一行地填充矩阵的。因此,如果读者需要自己定义一个矩阵时〈例如,自己构建用于空间变换的矩阵),就要注意这里的初始化方式。
类似地,当我们在CG 中访问一个矩阵中的元素时,也是按行来索引的。例如:
类似地,当我们在CG 中访问一个矩阵中的元素时,也是按行来索引的。例如:
- //按行优先的方式初始化矩阵M
- float3x3 M = float3x3(1.0, 2.0, 3.0,
- 4.0, 5.0, 6.0,
- 7.0, 8.0, 9.0);
- // 得到 M 的第一行,即( 1.0, 2.0, 3.0)
- float3 row= M[O];
- // 得到M 的第2 行第1 列的元素,即 4.0
- float ele = M[l][0];
如果读者熟悉Unity 的API,可能知道Unity 在脚本中提供了一种矩阵类型——Matrix4x4。脚本中的这个矩阵类型则是采用列优先的方式。这与Unity Shader 中的规定不一样,希望读者在遇到时不会感到困惑。
4.9.3 Unity 中的屏幕坐标: ComputeScreenPos/VPOS/WPOS
我们在4.6.8 节中讲了屏幕空间的转换细节。在写Shader 的过程中,我们有时候希望能够获得片元在屏幕上的像素位置。在顶点/片元着色器中,有两种方式来获得片元的屏幕坐标。
一种是在片元着色器的输入中声明VPOS 或WPOS 语义(关于什么是语义,可参见5.4 节)。
VPOS 是HLSL 中对屏幕坐标的语义,而WPOS 是CG 中对屏幕坐标的语义。两者在Unity Shader中是等价的。我们可以在HLSL/CG 中通过语义的方式来定义顶点/片元着色器的默认输入,而不需要自己定义输入输出的数据结构。这里的内容有一些超前,因为我们还没有具体讲解顶点/片元着色器的写法,读者在这里可以只关注VPOS 和WPOS 的语义。使用这种方法,可以在片元着色器中这样写:
- fixed4 frag(float4 sp : VPOS) : SV_Target
- {
- // 用屏幕坐标除以屏幕分辨率 _ScreenParams.xy,得到视口空间中的坐标
- return fixed4(sp.xy/_ScreenParams.xy, 0.0, l.0);
- }

另一种方式是通过Unity 提供的ComputeScreenPos 函数。这个函数在UnityCG.cginc 里被定义。通常的用法需要两个步骤,首先在顶点着色器中将ComputeScreenPos 的结果保存在输出结构体中,然后在片元着色器中进行一个齐次除法运算后得到视口空间下的坐标。例如:
- struct vertOut {
- float4 pos : SV_POSITION;
- float4 scrPos : TEXCOOROO;
- }
-
- vertOut vert(appdata_base v) {
- vertOut o;
- o.pos = mul(UNITY MATRIX_MVP, v.vertex);
- //第一步:把ComputeScreenPos 的结果保存到scrPos 中
- o.scrPos = ComputeScreenPos(o.pos);
- return o;
- }
-
- fixed4 frag(vertOut i) : SV_Target {
- //第二步: 用scrPos.xy 除以scrPos.w 得到视口空间中的坐标
- float2 wcoord = (i.scrPos.xy/i.scrPos.w);
- return fixed4(wcoord, 0.0, 1.0);
- }

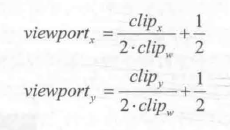
上面公式的思想就是,首先对裁剪空间下的坐标进行齐次除法,得到范围在[-1, 1 ] 的NDC,然后再将其映射到范围在[0, 1]的视口空间下的坐标。那么ComputeScreenPos 究竟是如何做到的呢?我们可以在UnityCG.cginc 文件中找到ComputeScreenPos 函数的定义。如下:
- inline float4 ComputeScreenPos (float4 pos) {
- float4 o = pos * O.5f;
- #if defined(UNITY_HALF_TEXEL_OFFSET)
- o.xy = float2(o.x, o.y* _ProjectionParams.x) + o.w * ScreenParams.zw;
- #else
- o.xy = float2(o.x, o.y* _ProjectionParams.x) + o.w;
- #endif
-
- o.zw = pos.zw;
- return o;
- }
UNITY_HALF_TEXEL_OFFSET 是Unity 在某些DirectX 平台上使用的宏,在这里我们可以忽略它。这样,我们可以只关注#else 的部分。_ProjectionParams.x 在默认情况下是1 (如果我们使用了一个翻转的投影矩阵的话就是 -1 ,但这种情况很少见〉。那么上述代码的过程实际是输出了:

可以看出,这里的 xy 并不是真正的视口空间下的坐标。因此,我们在片元着色器中再进行一步处理,即除以裁剪坐标的w 分量。至此,完成整个映射的过程。因此,虽然ComputeScreenPos的函数名字似乎意味着会直接得到屏幕空间中的位置,但并不是这样的,我们仍需在片元着色器中除以它的w 分量来得到真正的视口空间中的位置。那么,为什么Unity 不直接在ComputeScreenPos 中为我们进行除以w 分量这个步骤呢?为什么还需要我们来进行这个除法?这是因为,如果Unity 在顶点着色器中这么做的话,就会破坏插值的结果。我们知道,从顶点着色器到片元着色器的过程实际会有一个插值的过程(如果你忘了的话,可以回顾2.3.6 小节)。如果不在顶点着色器中进行这个除法, 保留x、y 和w 分量, 那么它们在插值后再进行这个除法,得到的x/w 和y/x 就是正确的(我们可以认为是除法抵消了插值的影响〉。但如果我们直接在顶点着色器中进行这个除法,那么就需要对x/w 和 y/w 直接进行插值,这样得到的插值结果就会不准确。原因是,我们不可以在投影空间中进行插值,因为这并不是一个线性空间, 而插值往往是线性的。
经过除法操作后,我们就可以得到该片元在视口空间中的坐标了,也就是一个xy 范围都在[0, 1]之间的值。那么它的zw 值是什么呢?可以看出,我们在顶点着色器中直接把裁剪空间的zw 值存进了输出结构体中, 因此片元着色器输入的就是这些插值后的裁剪空间中的zw 值。这意味着,如果使用的是透视投影,那么z 值的范围是[-Near, Far], w 值的范围是[Near, Far];如果使用的是正交投影,那么z 值范围是[-1 , 1 ],而w 值恒为1 。
经过除法操作后,我们就可以得到该片元在视口空间中的坐标了,也就是一个xy 范围都在[0, 1]之间的值。那么它的zw 值是什么呢?可以看出,我们在顶点着色器中直接把裁剪空间的zw 值存进了输出结构体中, 因此片元着色器输入的就是这些插值后的裁剪空间中的zw 值。这意味着,如果使用的是透视投影,那么z 值的范围是[-Near, Far], w 值的范围是[Near, Far];如果使用的是正交投影,那么z 值范围是[-1 , 1 ],而w 值恒为1 。
4.10 扩展阅读
计算机图形学使用的数学还有很多,本书仅涵盖了其中非常小的一部分。如果读者想要深入学习这些知识的话,书籍[1][2] 是非常好的图形学数学学习资料,读者可以在那里找到更多类型的变换及其数学表示。关于如何从左手坐标系转换到右手坐标系同时又保持视觉效果一样,可以参考资料[3]。关于如何得到线性的深度值可以参考资料[4] 。
[1] Fletcher Dunn, Ian Parberry. 3D Math Primer for Graphics and Game Development (2nd Edition). November 2, 2011 by A K Peters/CRC Press.
[2] Eric Lengyel. Mathematics for 3D game programming and computer graphics (3rd Edition). 2011 by Charles River Media。
[3] David Eberly. Conversion of Left-Handed Coordinates to Right-Handed Coordinates.
[4] http://www.humus.name/temp/Linearize%20depth.txt。
[1] Fletcher Dunn, Ian Parberry. 3D Math Primer for Graphics and Game Development (2nd Edition). November 2, 2011 by A K Peters/CRC Press.
[2] Eric Lengyel. Mathematics for 3D game programming and computer graphics (3rd Edition). 2011 by Charles River Media。
[3] David Eberly. Conversion of Left-Handed Coordinates to Right-Handed Coordinates.
[4] http://www.humus.name/temp/Linearize%20depth.txt。
4.11 练习题答案
4.2.5 节
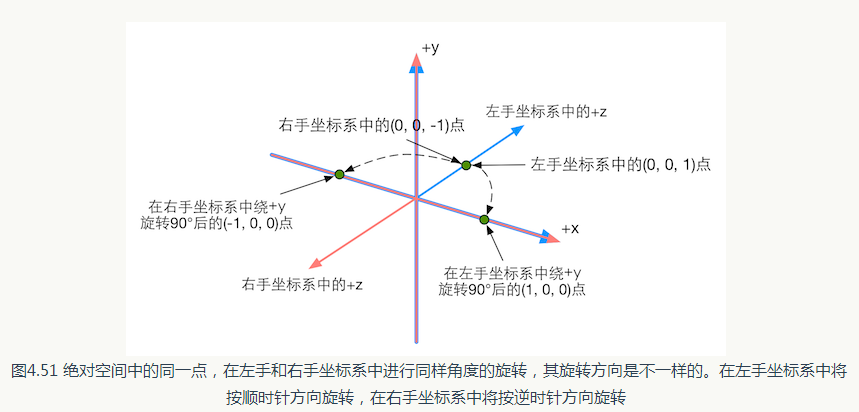
(1) 右手坐标系。(2) (1, 0, 0)。( 1,0,0)。从坐标表示来看,结果是完全一样的。左手坐标系和右手坐标系在绝大多数情况下不会对底层的数学运算造成影响,但是会在视觉表现上有所差异。以本题为例,虽然旋转之前点的坐标是一样的,但如果把它们统一在同一个空间中显示出来,其绝对位置是不同的。如图4.50 所示。
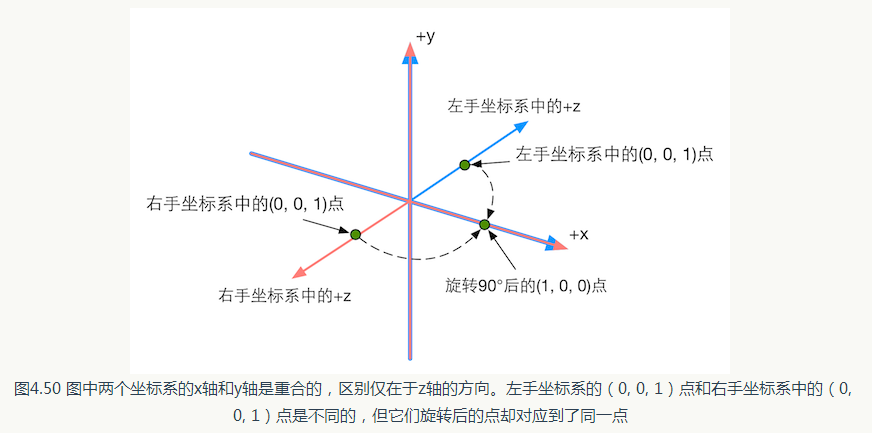
因此,如果我们想要在左手和右手坐标系中表示同一个点,就需要把其中一个坐标系中的表
示方法中的某个轴反向, 一般是把z 值取反。在本例中,左手坐标系的(0, 0, 1)点和右手坐标系中
的(0, 0, -1)点是同一点。但是,如果此时对该点再次分别在左手和右手坐标系中绕y 轴正方向旋
转90度,结果就不是同一个点了,如图4.51 所示。
(3)-10 。10。这是因为,在Unity 中,模型空间使用的是左手坐标系。球体所在的位置位于摄像机模型空间中的z 轴正方向,因此在模型空间下其z 值为10 。而观察空间使用的右手坐标系,摄像机的正前方是z 轴的负方向,因此在观察空间下其z 值为 -10 。
( 2 )正确。
( 3 )错误。坐标系的选择不会对底层的数学计算产生影响,对于叉积来说,我们总可以使用公式
4.3.3 节
1.
( 1 )错误,完全说反了。对于矢量来说它有两个属性: 模〈即大小〉束l方向, 矢量是没有位置属性的,也就是说,我们可以随意把它放在空间的任何位置。( 2 )正确。
( 3 )错误。坐标系的选择不会对底层的数学计算产生影响,对于叉积来说,我们总可以使用公式
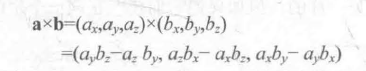
来计算。但是,不同的坐标系会影响最后的显示结果,即视觉上的表现。数学是一门非常严谨的学科, 但人类往往需要可视化一些东西,例如在屏幕上显示虚拟的三维空间,在把数字转换成视觉表现的时候,选择不同的坐标系可能会得到不同的结果。


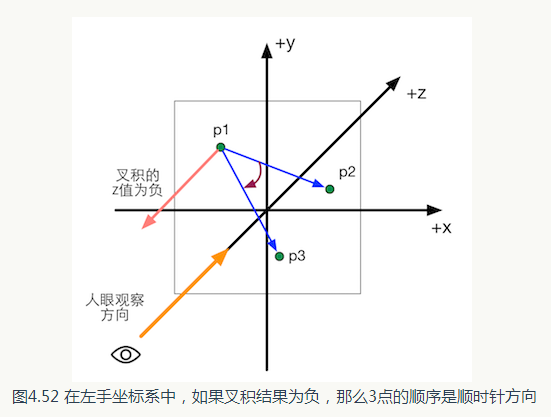


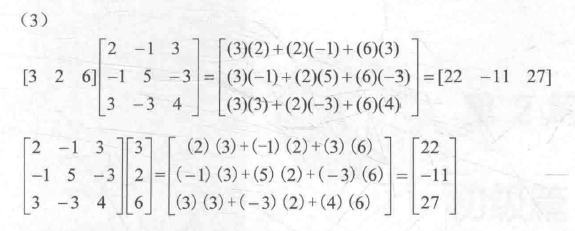
得到的结果转换成矢量都是(22,-11, 27),是一样的。这是因为, 该矩阵是一个对称矩阵
(symmetric matrix )。对称矩阵的转置是其本身,因此行矩阵和列矩阵不会对结果产生影响。
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/知新_RL/article/detail/107627
推荐阅读
相关标签


