线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化（上）_施密特正交化matlab

Gram-Schmidt正交化

        在前面的几个最小二乘的文章中，实际上已经看到Gram-Schmidt正交化的影子。在我个人看来，Gram-Schmidt正交化更像是专门为了简化最小二乘计算而量身定制的一种算法。下面，我会从最小二乘的经典应用 --- "拟合直线"开始，慢慢引出Gram-Schmidt的核心思想 ——> 那就是，究竟如何“改写”矩阵A中的列向量，才能在最大程度上简化最小二乘的求解过程呢？

---

Independent vectors(线性无关向量所组成的矩阵)

        很多关于最小二乘法的文章中都绕不开直线拟合问题，在讲Gram-Schmidt之前，让我们先从下面的例子开始：

        已知的三个数据点(当t1=1,b1=1),(当t2=3,b2=2)和(当t3=5,b3=4)，现在用这三个点去拟合一条直线b=C+Dt。首先根据这三个已知的数据点，可得到如下线性方程组：

根据方程组等式的左边部分，得到系数矩阵A(暂时先不考虑三个时间点所对应的值b)：

矩阵A的两个列向量的内积不为0，不正交（但，线性无关）

                

如下图所示：

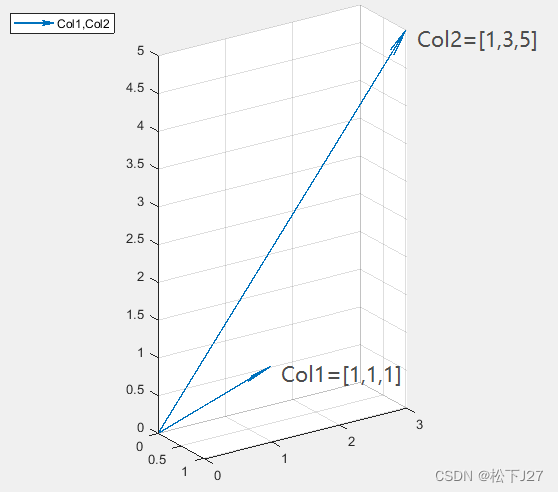
Matlab code:

close all
clear all
 
%时间t=[1 3 5]不在0的两侧，A中的两个列向量不正交，生成的A'A不是主对角线左右两边都是0的对角阵
A=[1 1 1;1 3 5]'
b=[1 2 4]'
 
col1=A(:,1)
col2=A(:,2)
 
col1'*col2
 
A'*A
 
%plot
X=[0,0];
Y=[0,0];
Z=[0,0];
U=[1,1];
V=[1,3];
W=[1,5];
 
quiver3(X,Y,Z,U,V,W,0,'LineWidth',1)
axis equal
legend('Col1,Col2','Location','northwest')

        且方程组的右端b=[1 2 4]不在A的列空间内，原方程组无解，需要通过最小二乘法来求近似解。套用最小二乘公式得到，其中与的逆分别为：

        

方程的近似解为：

套用公式，得到投影向量p为：

注意：如下图所示，col1和col2可以张成了一个二维平面，且由于方程组无解，所以b不在该平面内。但，b在该平面上的投影p在该平面内。

 ​​​​​

---

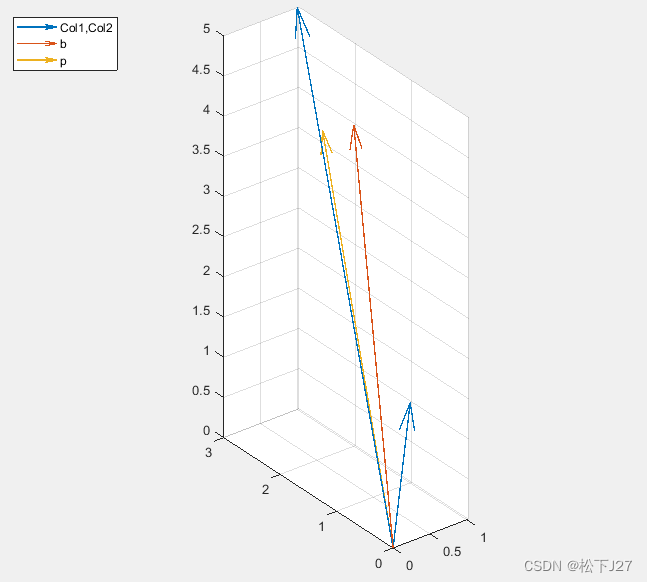
orthogonal vectors(正交向量组成的矩阵)

        为了让正规方程更好求解，我们把原有的t=(1,3,5)减去均值3，变成T=(-2,0,2)，矩阵A也变成了：

新矩阵中的两个列向量的内积为0，矩阵A的两个列向量也从非正交变成了正交

              

如下图所示：  

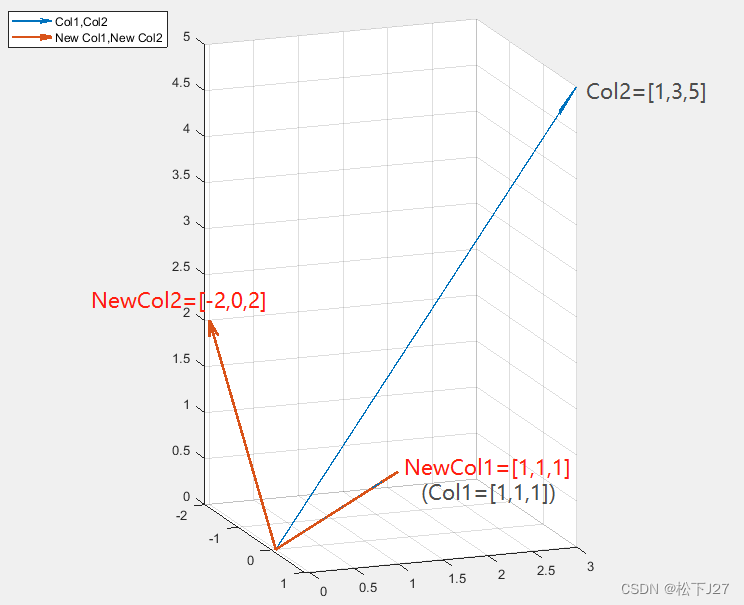
Matlab code:

%时间t=[-2 0 2]位于0的两侧对称，A中的两个列向量彼此正交，A'A可以生成主对角线左右两边都是0的对角阵
A=[1 1 1;-2 0 2]'
 
col1=A(:,1)
col2=A(:,2)
 
col1'*col2
 
A'*A
 
%plot
Q1=[1,-2];
Q2=[1,0];
Q3=[1,2];
hold on
quiver3(X,Y,Z,Q1,Q2,Q3,0,'LineWidth',2)
 
legend('Col1,Col2','New Col1,New Col2','Location','northwest')

同时，我们还发现，如果矩阵A中的列向量彼此正交，最小二乘公式中的 就变成了对角阵：

   

---

 补充：

且对角阵有如下性质：

---

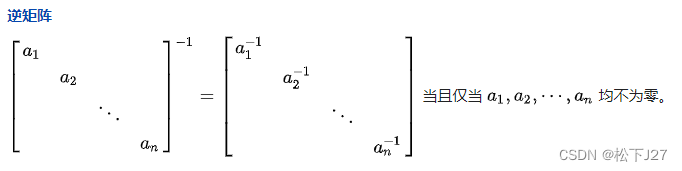
        这就是说，通过这一步对矩阵A的改变，达到了简化了求解近似解的目的，同时也简化了投影向量p的计算。因为为对角阵，所以我们可以直接写出的逆，即，直接取所有对角线元素的倒数：

方程的近似解，也变成了(和之前求出的结果不同)：

套用公式，投影p仍然是（p的计算也同时被简化了）：

        可见，通过对A的修改可实现最小二乘的快速求解。如此一来，就不再需要机械的套用公式，而是直接求解简化后的正规方程，就能得到答案，同时也避免了求的逆，这种精度误差较大的运算。

        注意：矩阵A的改变虽然改变了，但投影p不变。这说明，矩阵A的变化并没有改变A的列空间，即从A=[1 1 1;；1 3 5]'到A=[1 1 1；-2 0 2]'，矩阵的A的列空间是一样的。因为，如果对他们进行高斯消元，得到的最简行阶梯矩阵是一样的=[1 0 0,0 1 0]'。

---

 orthogonal unit vectors(归一化后的正交向量所组成的矩阵)

        更进一步，如果我们把A中的两个已经彼此正交的列向量(orthogonal vectors)都变成单位正交向量(orthogonal unit vectors)，则会从对角阵变成单位矩阵I，的逆也变成了单位矩阵。

        把矩阵A中已经彼此正交的向量，变成单位正交向量的方法是：把A中的每一个向量进行单位化（也叫归一化），即，该向量除以这个向量自身的长度。

根据向量长度的计算公式，列向量col1的长度为，col2的长度为，归一化后有：

 

内积为0，彼此正交： 

        

如下图所示：     

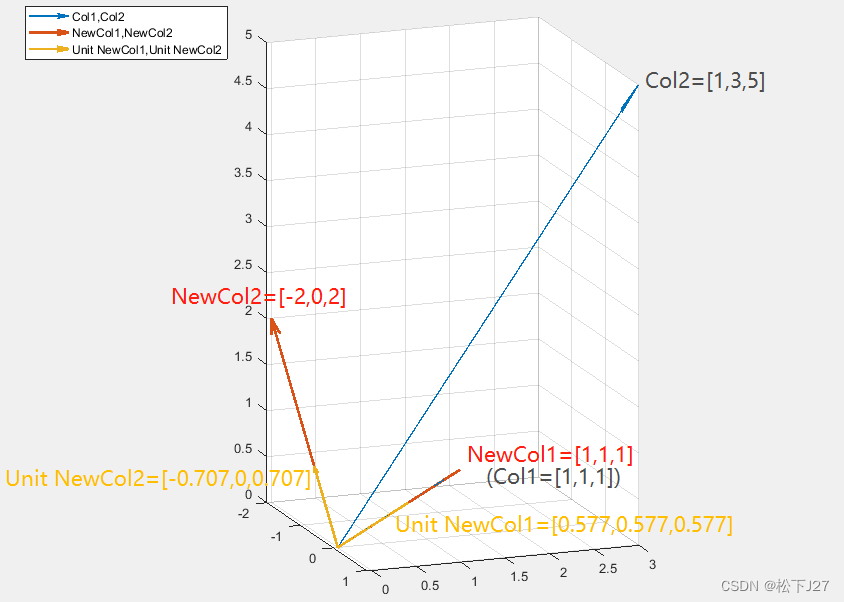
Matlab code:

%把矩阵A中的两个相互正交的列向量变成单位向量，这样一来，A也变成了标准正交矩阵
Length_Col1 = sqrt(sum(col1.^2));
Length_Col2 = sqrt(sum(col2.^2));
col1_unit=col1./Length_Col1
col2_unit=col2./Length_Col2
 
A_unit=[col1_unit col2_unit]
 
% check:对于标准正交矩阵而言，有A'A=I
A_unit'*A_unit
 
%plot
Q1=[1/Length_Col1,-2/Length_Col2];
Q2=[1/Length_Col1,0/Length_Col2];
Q3=[1/Length_Col1,2/Length_Col2];
hold on
quiver3(X,Y,Z,Q1,Q2,Q3,0,'LineWidth',2)
 
legend('Col1,Col2','NewCol1,NewCol2','Unit NewCol1,Unit NewCol2','Location','northwest')

单位化后，矩阵A又变成了矩阵：

还有新的方程：(注意：为了维持原方程组Ax=b中的A变成后，方程左右两边保持不变，原方程中的x也要改，变成)

 

现在，基于这个新矩阵生成正规方程，右边的计算结果就是单位矩阵I：

正规方程左边：

也就是说，当矩阵A中的列向量变成单位正交向量后，极大的简化了近似解的计算。因为为单位矩阵，使得原来的正规方程变成了：

与此同时，近似解的计算公式也被极大地简化了：

最终得到的答案和之前一样：

      在本例中，归一化后的两个相互正交的单位列向量和是一组标准正交基。

Matlab code:

%% 用简化后的公式计算正规方程的解
%x=Q'b
x=A_unit'*b
 
x_new=[x(1)/Length_Col1; x(2)/Length_Col2]
 
%P=QQ'
P=A_unit*A_unit'
 
%projection p=QQ'b
p=P*b

---

标准正交基(Orthonormal Bases)

现在，我们给出关于标准正交基Orthonormal的正式定义：

        如果一组列向量，他们满足彼此之间的内积为0(正交性)，且，他们的长度都为1(归一化)。则，我们把这样的一组列向量称为标准正交基Orthonomal。同时，我们也把由标准正交基组成的矩阵用大写的英文字母Q来表示。

        对于标准正交基而言，一个最常见的例子就是x-y二维坐标系。x轴和y轴不仅相互垂直，坐标轴上的每一个刻度都是该轴所对应的单位向量的长度的倍数(如果用q1=(1,0)表示x轴的单位向量，用q2=(0,1)表示y轴的单位向量的话)。q1和q2共同组成了一个2x2矩阵Q，这是一个2x2的单位矩阵。

        对于n维空间，同样有n个坐标轴e1,e2,....en，他们也是一组标准正交基，且他们所组成的矩阵Q也是一个单位阵。

---

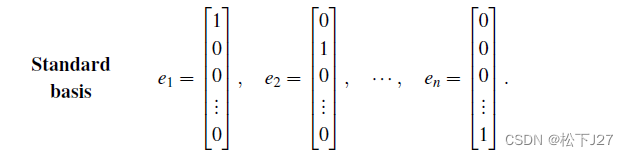
标准正交矩阵Q(Orthogonal Matrices)

        我们把用标准正交基q1,q2...qn所组成的矩阵称为标准正交矩阵Q，Q可以是方阵也可以不是方阵。且，。

如果标准正交矩阵Q是一个方阵的话，则有：

也就是说，如果方阵Q是一个标准正交矩阵，则方阵Q的转置就是Q的逆矩阵。

 

例：任何置换矩阵P(permutation matrix)都是一个标准正交矩阵。

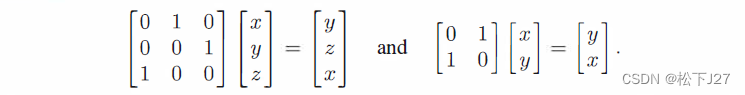
         上图的两个置换矩阵，分别交换了(x,y,z)的位置和交换了(x,y)的位置。由于，这两个置换矩阵P的列向量都是单位向量，且彼此两两正交，所以是标准正交矩阵。

        最后，在这里补充一条标准正交矩阵Q的又一条重要性质，即，用一个标准正交矩阵Q去乘一个任意向量都不会改变这个向量的长度。（书上上，这一性质还挺重要的，只是我暂时没发现）

---

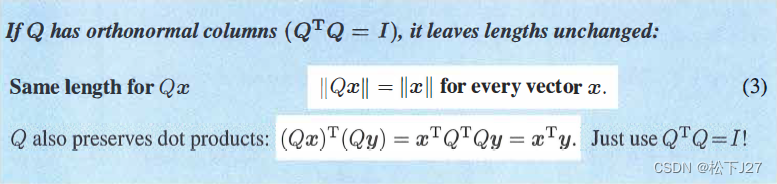
标准正交矩阵的投影与最小二乘

        对于一个mxn的矩阵A，如果矩阵A中的列向量都彼此正交，且向量长度都是1。则A是一个标准正交矩阵。若方程组Ax=b无解，则需要根据最小二乘的计算公式分别计算和。但如果A是标准正交矩阵Q的话，或者说，如果我们预先把原本不是标准正交矩阵的矩阵A变成标准正交矩阵Q的话，就能极大的简化最小二乘的计算。如下图所示，下图中横线处都是原来需要计算的部分，因为标准正交矩阵的性质，都变成了单位矩阵I，等同于不再需要计算了。

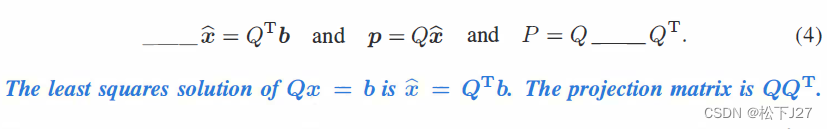
也就是说，如果我们能够在计算任意矩阵A的最小二乘解之前，预先把A改造成标准正交矩阵Q，则能够带来以下的一些计算上的简化与便利。：

第一：他极大地简化了正规方程的表达式，同时，直接给出了最小二乘解。

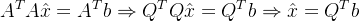（正规方程）

第二：他简化了所有包含的计算，同时，更重要的是他也避免了求的逆。

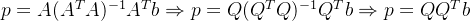（投影）

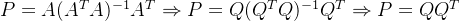 （投影矩阵）

---

标准正交矩阵的几何表示

        标准正交矩阵Q所带来的影响，并不仅仅体现在简化计算公式上，在投影的几何表示上也有相应的体现。当A为正交矩阵Q时，向量的投影()可写成在每一个列向量上的投影的和的形式：

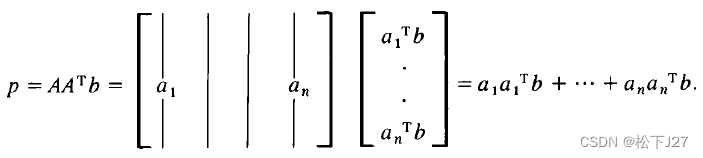
 其中：

        

依此类推。。。

        

令b=(b1,b2,...,bn),则有：

        

 依此类推。。。

用几何图像来表示就是：

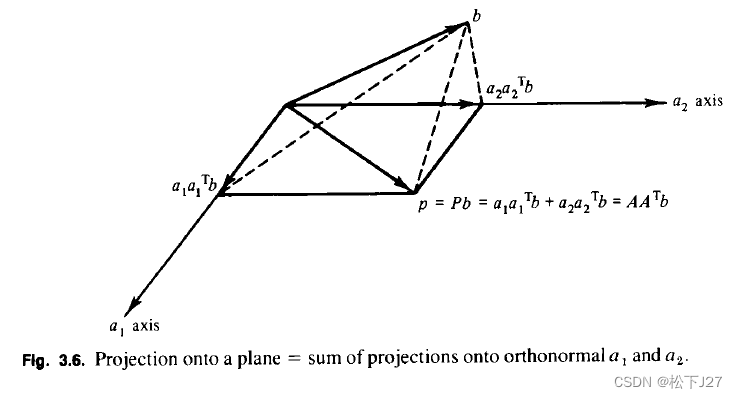
也就是说，向量b在A所张成的列空间上的投影p等于，b在每个坐标轴上的投影的和。

        此外，当A为标准正交矩阵时(当A为方阵时,m=n)，A中的列向量可以张满整个。A中的每个列向量，实际上就是n维正交坐标系中的每个轴所对应的单位向量。对于中的任意一个向量b，b在A的列空间内，所以可以写成Ax=b的形式，x中的每个元素都是A中各列所对应的权重。当A为Q时，我们把Qx=b写成如下形式：

 

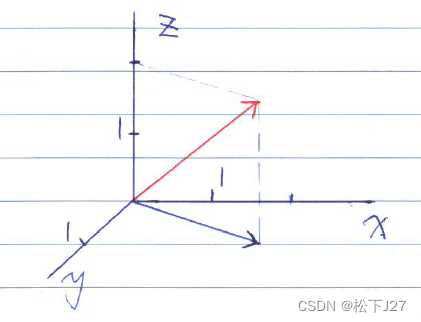
q1,q2,...,qn分别表示n维坐标系中的每个坐标轴上的单位向量，这样一来，上式所表示的就是，在n维直角坐标系中，任意一个向量b等于，他在q1轴，q2轴，。。。qn轴上分量的和。

例如：

当x=1.5,y=1,z=2时有。

小结：

1,        给定的mxn方程组 Ax=b 无解

2,        左右两边同时乘以，得到正规方程

3,        求解正规方程，得到

4,        若A是一个标准正交矩阵Q，则改Ax=b为Qx=b

5,        左右两边同时乘以,得到新的正规方程

6,        极大的简化了原来计算，得到

7,        与此同时，也简化了投影p的计算，得到

---

 （全文完）

作者 --- 松下J27

参考文献(鸣谢)：

1，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang

2，线性代数及其应用，候自新，南开大学出版社 1990

3，Linear Algebra and Its Applications, Second Edition, Gilbert Strang, 1980

4，Linear Algebra and Its Applications, Fourth Edition, Gilbert Strang, 2005

增加了插图和对应的matlab代码，2023/05/24

对全文进行了大量的修改。2023/06/25

对文章开始处的例子进行了进一步的修改。2023/10/10

古诗词赏析：

《左迁至蓝关示侄孙湘》

唐---韩愈

一封朝奏九重天，夕贬潮州路八千。
欲为圣明除弊事，肯将衰朽惜残年！
云横秦岭家何在？雪拥蓝关马不前。
知汝远来应有意，好收吾骨瘴江边。

（配图与本文无关）

版权声明：文中的部分图片，文字或者其他素材，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27