Matlab机器人工具箱（2-3）：一些demo（轨迹规划）_怎么将字转换为puma560机器人末端执行器的轨迹

01 轨迹规划函数（关节空间和笛卡尔）

%运动学轨迹
mdl_puma560%调出puma560 DH模型作为实验对象
t=[0:0.05:2];%两秒完成轨迹，步长0.05
%关节运动（产生两位置间路径，结果表达为一系列中间点的关节角度）
%产生位姿矩阵法1：直接给出关节角度
%T1 = p560.fkine([0 0 0 0 0 0]);%生成一个位姿
%T2 = p560.fkine([pi 0 0 0 0 0]);%生成一个位姿
%产生位姿矩阵法2：描述位置
T1 = transl(0.4,0.2,0)*trotx(pi);%位移*旋转,创建齐次变换
T2 = transl(0.4,-0.2,0)*trotx(pi/2);
q=p560.jtraj(T1,T2,t);%输入SE3 or 4*4变换矩阵，生成轨迹
p560.plot(q)%绘制轨迹
%笛卡尔运动
%笛卡尔空间中直线运动,生成从SE3空间两点间直线的一系列中间位置，结果表达为4*4齐次换矩阵
Ts=ctraj(T1,T2,length(t));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

代码详解：
利用Robotics Toolbox提供的ctraj和jtraj函数可以实现笛卡尔规划和关节空间规划。

其中ctraj函数的调用格式：

• TC = CTRAJ(T0, T1, N)
• TC = CTRAJ(T0, T1, R)
  说明：
  参数TC为从T0到T1的笛卡尔规划轨迹，N为点的数量，R为给定路径距离向量，R的每个值必须在0到1之间。

其中jtraj函数的调用格式：

• [Q QD QDD] = JTRAJ(Q0, Q1, N)
• [Q QD QDD] = JTRAJ(Q0, Q1, N, QD0, QD1)
• [Q QD QDD] = JTRAJ(Q0, Q1, T)
• [Q QD QDD] = JTRAJ(Q0, Q1, T, QD0, QD1)
  说明：
  参数Q为从状态Q0到Q1的关节空间规划轨迹，N为规划的点数，T为给定的时间向量的长度，速度非零边界可以用QD0和QD1来指定。QD和QDD为返回的规划轨迹的速度和加速度。

02 关节空间和笛卡尔空间的轨迹规划（对比）

1. qq=jtraj=(q1,q2,t)
2. qT=p560.jtraj(T1,T2,t)
3. Ts=ctraj(T1,T2,length(t));

①和②是关节规划的函数，③是笛卡尔规划的函数。
①②是先根据首尾位姿，求出关节角度，再规划
③是根据首尾位姿，求轨迹，再逆解得到关节角度

①的参数是关节角度，②的参数是位姿矩阵

clc
clear

mdl_puma560%调出puma560 DH模型作为实验对象
t=[0:0.05:2];%两秒完成轨迹，步长0.05

T1 = transl(0.4,0.2,0)*trotx(pi);%位移*旋转,创建齐次变换
T2 = transl(0.4,-0.2,0)*trotx(pi/2);

q1 = p560.ikine6s(T1);%根据末端位姿，求各关节
q2 = p560.ikine6s(T2);

qq=jtraj(q1,q2,t);%根据各关节，生成轨迹
Tqq=p560.fkine(qq);

qT=p560.jtraj(T1,T2,t);%根据位姿矩阵，生成轨迹
Tqt=p560.fkine(qT);

%笛卡尔运动
%笛卡尔空间中直线运动,生成从SE3空间两点间直线的一系列中间位置，结果表达为4*4齐次换矩阵
Ts=ctraj(T1,T2,length(t));
qs=p560.ikine6s(Ts);

figure(1)%绘制各关节角度
for i=1:6
      subplot(2,3,i)
      plot(t, qq(:,i))
      hold on;
      plot(t, qT(:,i))
      plot(t, qs(:,i)) 
      legend('关节空间-根据各关节规划','关节空间-根据位姿规划','笛卡尔空间')
      hold off;
end

figure(2)
pq=transl(Tqq);%提取旋转矩阵中的位移部分
pT=transl(Tqt);
ps=transl(Ts);
%依次是 '关节空间-根据各关节规划','关节空间-根据位姿规划','笛卡尔空间'
subplot(3,1,1)
plot3(pq(:,1),pq(:,2),pq(:,3))
subplot(3,1,2)
plot3(pT(:,1),pT(:,2),pT(:,3))
subplot(3,1,3)
plot3(ps(:,1),ps(:,2),ps(:,3))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

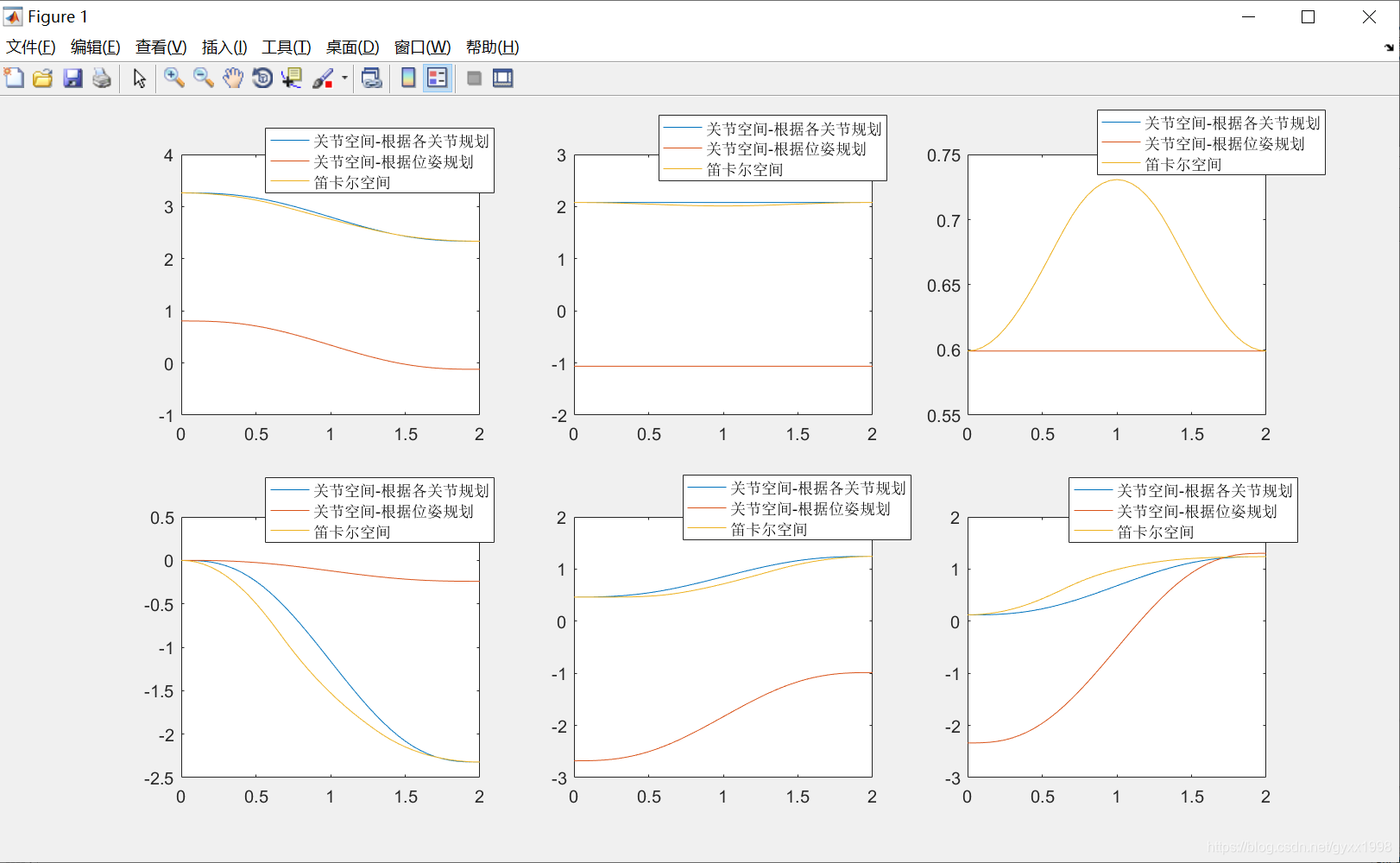
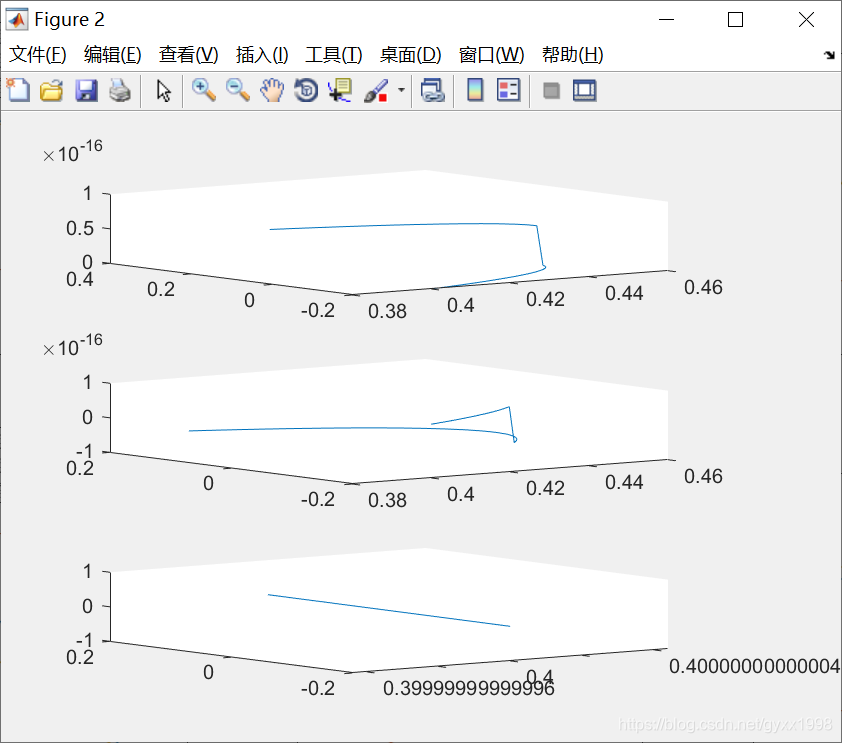
对比结果：
就关节角度而言，以关节为参数的关节规划 和 笛卡尔轨迹规划 结果较为相近；
而 以位姿矩阵为参数的关节规划 与以上二者相差较远

03 关节空间的平滑移动（jtraj vs. mtraj）

关节空间运动：将机器人末端执行器平滑地从A点移动到B点
参考资料：
中正平和的机器人学笔记——3.几个MATLAB实例https://blog.csdn.net/qq_34265512/article/details/84894716

全部代码：

mdl_puma560  %载入提供的puma560机械臂模型

%设置位姿矩阵
T1 = transl(0.4, 0.2, 0) * trotx(pi);
T2 = transl(0.4, -0.2, 0) * trotx(pi/2);

%得到对应关节坐标
q1 = p560.ikine6s(T1);
q2 = p560.ikine6s(T2);

%设置时间向量
t = [0:0.05:2];

%进行平滑插值，得到空间轨迹
q = jtraj(q1, q2, t);

figure(1);
p560.plot(q) %绘制运动轨迹，如图1
figure(2);
plot(t, q) %绘制关节角随时间的变化，如图2

T = p560.fkine(q); %得到笛卡尔轨迹
p = transl(T);%轨迹的位移部分

figure(3);
plot(p(:,1),p(:,2)) %绘制xy平面内的末端轨迹，如图3
figure(4);
plot(t, tr2rpy(T)) %画出另一种位姿表达（Roll、Pitch、Yaw），如图4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

运行效果：

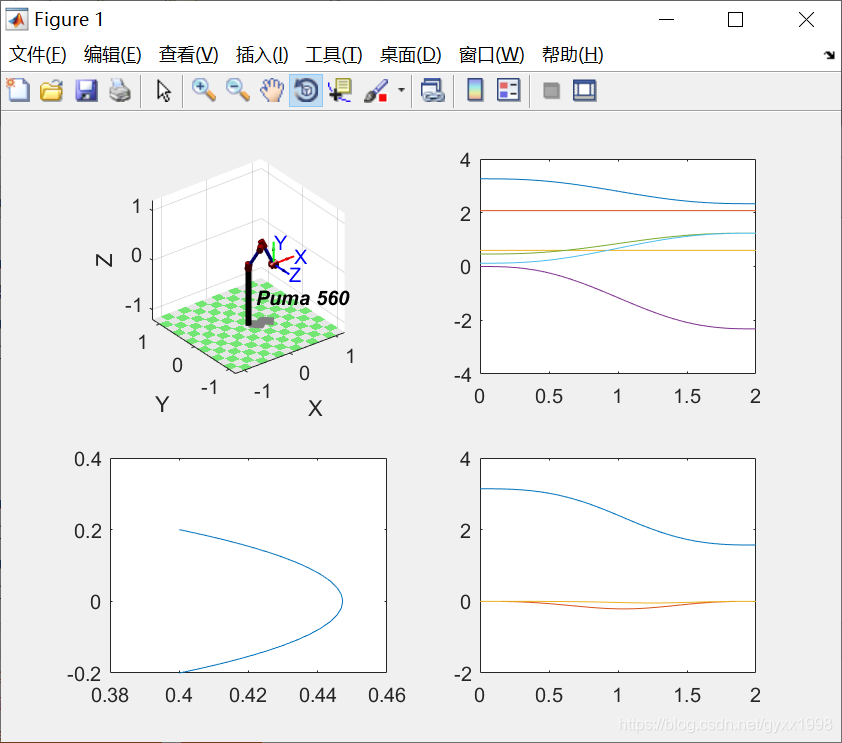
↑ 运动轨迹绘制 ↑ 关节随时间变化 ↑ xy平面-末端轨迹 ↑ Roll-Pitch-Yaw下的姿态 ↑

代码详解：
将机器人末端执行器平滑地从A点移动到B点，更为准确的说，应当说从位姿A移动到位姿B
① 设置起始点与目标点的位姿矩阵

T1 = transl(0.4, 0.2, 0) * trotx(pi);
T2 = transl(0.4, -0.2, 0) * trotx(pi/2);
1
2

根据位姿矩阵可以确定关节坐标

q1 = p560.ikine6s(T1);
q2 = p560.ikine6s(T2);
1
2

② 对两个位姿之间进行平滑插值，得到一个关节空间轨迹

%设置时间向量
t = [0:0.05:2];
1
2

写法1：
具有tpoly插值的mtraj函数

%q = mtraj(@tpoly, q1, q2, t);
%q = mtraj(@lspb, q1, q2, t);
%[q,qd,qdd] = jtraj(q1, q2, t);
1
2
3

写法2：
jtraj相当于具有tpoly插值的mtraj
但优化了多轴情况，且允许使用额外参数设置v0和vt

q = jtraj(q1, q2, qt); 
1

写法3：
以下是SerialLink类提供的jtraj更简便的用法，不需要确定关节坐标，可以直接使用位姿矩阵作为函数变量

q = p560.jtraj(T1, T2, t);
1

③得到运动轨迹并绘制，同时绘制关节角变化

figure(1);
p560.plot(q) %绘制运动轨迹，如图1
figure(2);
plot(t, q) %绘制关节角随时间的变化，如图2

T = p560.fkine(q); %得到笛卡尔轨迹
p = transl(T);%轨迹的位移部分
figure(3);
plot(p(:,1),p(:,2)) %绘制xy平面内的轨迹，如图3
figure(4);
plot(t, tr2rpy(T)) %画出另一种位姿表达，如图4
1
2
3
4
5
6
7
8
9
10
11

直线轨迹规划 (从 jtraj 到 ctraj)

使用 jtraj函数 做的这条轨迹不是一条直线，因为我们只给了机器人初始点和结束点两个坐标，因此机器人在运动时，转动关节，末端执行器的轨迹是弧线
为了使机器人末端在笛卡尔空间中也划出一条直线轨迹，可以将原来的jtraj函数换成ctraj

Ts = ctraj(T1, T2, length(t));

figure(1)
plot(t, transl(Ts) )

figure(2)
plot(t, tr2rpy(Ts) )
qc = p560.ikine6s(Ts);

figure(3)
plot(t,q)

figure(4)
p560.plot(qc)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

04 多段连续轨迹

参考资料：
中正平和的机器人学笔记——3.几个MATLAB实例https://blog.csdn.net/qq_34265512/article/details/84894716
让机器人画出一个字母“E”：

%让机器人画出一个字母“E”

mdl_puma560  %载入提供的puma560机械臂模型

%字母E的途径点
path = [1 0 1
1 0 0
0 0 0
0 2 0
1 2 0
1 2 1
0 1 1
0 1 0
1 1 0
1 1 1];

%分段路径可绘制如下
figure(1);
plot3(path(:,1), path(:,2), path(:,3), 'color', 'k', 'Linewidth', 2);
hold on

%将其转化为连续路径
p=mstraj(path, [10 10 10], [], [2 2 2], 0.02, 0.01);
%第二个参数规定了xyz三个方向上的最大速度
%第四个参数规定了初始坐标、采样间隔、加速时间

path=0.1*path;

%给出字母的起点
Tp = transl(0.1*p);
Tp = homtrans( transl(0.4, 0, 0), Tp);
%Tp是一系列的齐次变换矩阵，代表了路径上每一个点的位姿

%通过逆运动学求出一系列关节坐标
p560.tool = trotx(pi); %考虑姿态，保证z轴向下
q = p560.ikine6s(Tp);
%figure(2)
p560.plot(q)  %绘制出动画


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

运行效果：

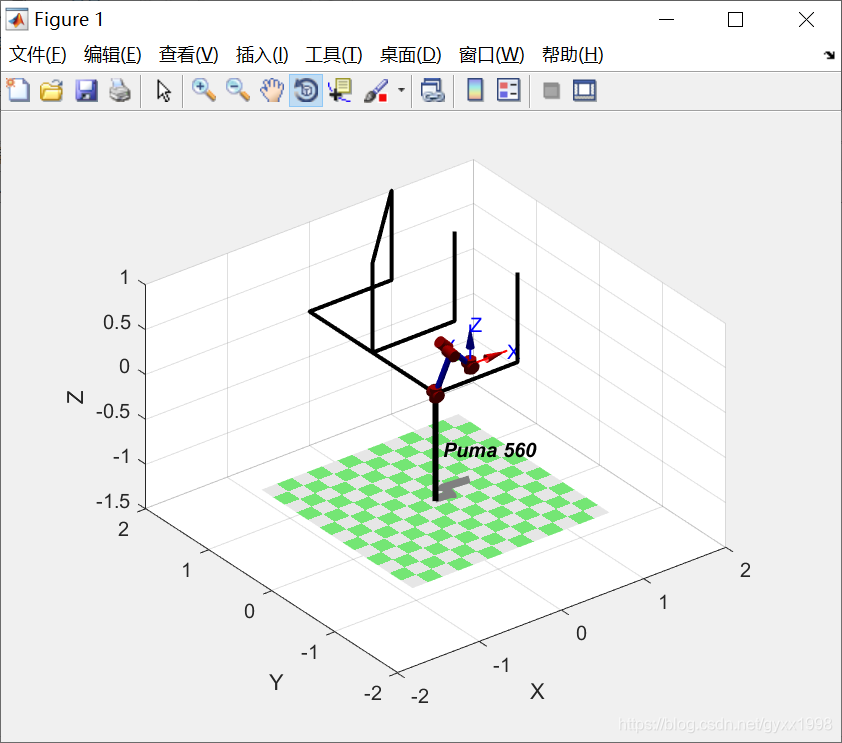
还有一个问题：用plot3绘制的Path轨迹和动画里末端执行器运动的不一样？是刻度的问题吗
对此，我做出了一点改进，让绘制的Path与末端执行器的一致

clear
clc

mdl_puma560  %载入提供的puma560机械臂模型

%字母E的途径点
path = [1 0 1
1 0 0
0 0 0
0 2 0
1 2 0
1 2 1
0 1 1
0 1 0
1 1 0
1 1 1];

%将其转化为连续路径
p=mstraj(path, [10 10 10], [], [2 2 2], 0.02, 0.01);
%第二个参数规定了xyz三个方向上的最大速度
%第四个参数规定了初始坐标、采样间隔、加速时间

%齐次变换，将0.1*p产生的向量投影到（0.4,0，0）的坐标系下
Tp = transl(0.1*p);
Tp = homtrans( transl(0.4, 0, 0), Tp);
%Tp是一系列的齐次变换矩阵，代表了路径上每一个点的位姿

path2=transl(Tp);%提取旋转矩阵中的平移部分
plot3(path2(:,1), path2(:,2), path2(:,3), 'color', 'k', 'Linewidth', 2);
hold on

%通过逆运动学求出一系列关节坐标
p560.tool = trotx(pi); %考虑姿态，保证z轴向下
q = p560.ikine6s(Tp);
p560.plot(q)  %绘制出动画
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

对以上代码解释如下：
这个代码与原代码的主要区别就是绘制的Path2就是根据末端执行器的轨迹Tp所画

• Tp = transl(0.1*p)：直接使用Path部分，则会超出工作范围
• Tp = homtrans( transl(0.4, 0, 0), Tp)：homtrans可以理解为将后一参数投影到前一参数的坐标系下，即旋转矩阵Tp在(0.4, 0, 0)坐标系下的表示方法
  为什么Tp而不是p呢？因为homtrans可以两个参数前者是矩阵，后者向量。但我们之后进行逆运动学的时候，是需要矩阵，而非向量呀。
  为什么 transl(0.4, 0, 0)而不是相对于原点呢？因为关节原点一般不好抓取，一般抓取的都是距离原点一段距离的地方。如果直接是原点，逆运动学解可能求不出来。所以我们设置画“E”型轨迹的地方的原点为(0.4, 0, 0)
• path2=transl(Tp)：Tp是位姿矩阵，不能直接用来画轨迹图，所以我们用transl函数提取其中的位移部分

类似的一个根据路径进行运动的例子：

clear all
clc
mdl_puma560
path=[0 0 0;0 1 0;0 1 1;1 1 1];

plot3(path(:,1), path(:,2), path(:,3), 'color', 'k', 'Linewidth', 2);
hold on;
p=mstraj(path,[2,2,2],[],[2 2 2],0.02,0.1);
Tp=transl(0.1*p);
Tp=homtrans(transl(0.2,0.2,0.1),Tp);
q=p560.ikine6s(Tp);
p560.plot(q);
1
2
3
4
5
6
7
8
9
10
11
12

代码详解：
①设置路径Path（N×3）
②p=matraj函数 设置起始点、最大速度、采样时间等
③齐次变换 ：transl和homtrans函数
④求反解：ikine6s
⑤plot绘制动画

05 位姿描述（更好理解homtrans函数）

参考资料：https://www.csdn.net/gather_2b/MtzaIgysMzc5LWJsb2cO0O0O.html

二维

clc
clear all
%% 二维空间位姿描述
T1=se2(1,2,30*pi/180);       %建立齐次坐标变换，代表（1,2）的平移和30°的旋转
trplot2(T1,'frame','1','color','b')%绘制变换坐标系，名字：{1} 颜色：蓝色 
axis([0 5 0 5]);%坐标轴范围x为0-5 y为0-5

T2=se2(2,1,0);   %齐次坐标变换：平移（2,1）零旋转的相对位姿
hold on 
trplot2(T2,'frame','2','color','r');%绘制变换坐标系，名字：{2} 颜色：红色

T3=T1*T2;
trplot2(T3,'frame','3','color','g');%绘制复合坐标系，名字：{3} 颜色：绿色

T4=T2*T1;
trplot2(T4,'frame','4','color','c');

p=[3;2];%相对世界坐标系定义点（3,2）
plot_point(p,'*')%把p点用*表示在图中

%通过附加一个1 将欧几里得点转换为齐次形式
p1=inv(T1)*[p;1]       %p点相对于坐标系{1}的坐标，（得到结果为齐次坐标）
inv(T1)*e2h(p)         %另一种写法,p点相对于坐标系{1}的坐标（得到结果为齐次坐标）

%辅助函数e2h将欧几里得坐标点转换为齐次形式，而h2e进行逆转换
%一个负的y坐标，使用h2e函数可以进行反变换
h2e(inv(T1)*e2h(p))    %将齐次形式转换为欧几里得点，（得到结果为欧几里得坐标）
homtrans(inv(T1),p)    %上一句话的更简洁的表达式，（得到结果为欧几里得坐标）

p2=homtrans(inv(T2),p)  %p点相对于坐标系{2}的描述==>p2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

代码详解：

①se2函数：得到二维位姿矩阵（齐次形式）
②trplot2：绘制二维坐标系
③plot_point：绘制一个点
④ inv(T1)*e2h ( p) 等价于 inv(T1) *[p;1] ：将p（2×1）转化为为齐次形式（3×1），以便于旋转矩阵相乘
⑤h2e(inv(T1)*e2h( p)) 等价于 homtrans(inv(T1),p) ：h2e进行反变换，将齐次形式转为欧几里得。homtrans函数的使用更加简单，将p（2×1）投影到 T1（3×3）的坐标下，得到在其坐标系下的欧几里得坐标

三维

%% 三维空间位姿描述

R1 = rotx(pi/2)% 表示x轴的旋转矩阵
R2 = roty(pi/2)% 表示y轴的旋转矩阵
R3 = rotz(pi/2)% 表示z轴的旋转矩阵
trplot(R3,'frame','1','color','r') % 绘制坐标系
grid on
tranimate(R3) %旋转动画，展示世界坐标系旋转到指定坐标系的过程
T=transl(1,0,0)*trotx(pi/2)*transl(0,1,0)
t2r(T)  %提取矩阵中旋转矩阵部分
transl(T)  %提取矩阵中平移部分
1
2
3
4
5
6
7
8
9
10
11

代码详解：

①trplot：绘制三维坐标系
②tranimate：旋转动画，展示世界坐标系旋转到指定坐标系的过程
③t2r：提取矩阵中旋转矩阵部分（3×3）
④transl：提取矩阵中平移部分（3×1）

06 轨迹规划（五次多项式 vs 带抛物线过渡的直线）

二维：

五次多项式轨迹

%% 五次多项式轨迹
%限制条件为：起始终止速度、加速度为0，起点终点设定。六个条件
s=tpoly(0,1,50);   %生成一个五次多项式轨迹，返回50*1列向量，其值在0-1范围内分50个时间步平滑变化
[s,sd,sdd]=tpoly(0,1,50);		%相应的速度(sd)加速度(sdd)通过增加输出选项参数返回
subplot(3,1,1) 		
plot(s);xlabel('Time'); ylabel('s');			%绘制轨迹曲线
subplot(3,1,2)
plot(sd);xlabel('Time'); ylabel('sd');		%绘制速度曲线
subplot(3,1,3)
plot(sdd);xlabel('Time'); ylabel('sdd');		%绘制加速度曲线
%s=tpoly(0,1,50,0.5,0)		%初始速度和终点速度默认值为0，也可设置非零值。初始速度0.5，最终速度0
mean(sd)/max(sd)		%计算平均速度
1
2
3
4
5
6
7
8
9
10
11
12

运行效果

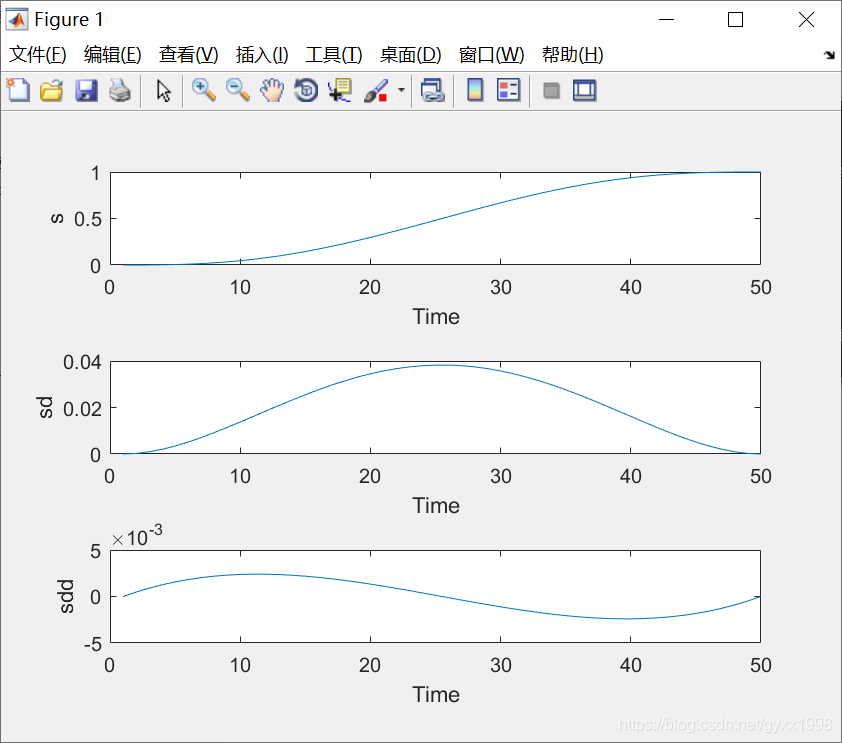
抛物线轨迹规划

s=lspb(0,1,50)
[s,sd,sdd]=lspb(0,1,50);       %参数与tpoly中的含义相同
subplot(3,1,1) 		%绘制轨迹曲线
plot(s);xlabel('Time'); ylabel('s');
subplot(3,1,2)
plot(sd);xlabel('Time'); ylabel('sd');
subplot(3,1,3)
plot(sdd);xlabel('Time'); ylabel('sdd');
max(sd)     %函数lspb自动生成的直线段速度
s=lspb(0,1,50,0.025);   %可以通过第四个输入参数为直线段指定一个速度
1
2
3
4
5
6
7
8
9
10

运行效果

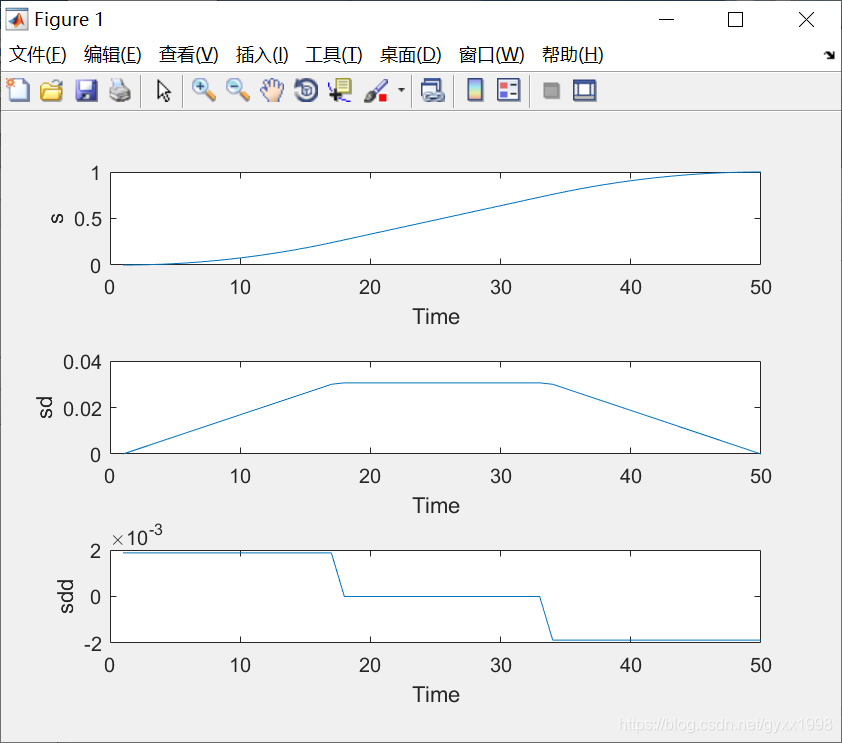
代码详解：

• 五次多项式轨迹
  从时间标量函数开始。这种函数的初始值和最终值是确定的，函数是光滑的（低阶时间导数是连续的，速度加速度是连续的，有时加速度的导数或加速度率也需要连续）
  比较常用的五次多项式：
  ①s=tpoly(0,1,50); %生成一个五次多项式轨迹，返回50*1列向量，其值在0-1范围内分50个时间步平滑变化
  ② [s,sd,sdd]=tpoly(0,1,50); %相应的速度(sd)加速度(sdd)通过增加输出选项参数返回

• 带抛物线过渡的直线轨迹
  每个机器人关节都有一个额定的最大速度，为了使关节运动时间最短，应该使运行在最大速度上的时间尽可能长，尽可能希望速度曲线顶部是一条平直线
  一种公认的较理想的选择是采用混合曲线轨迹，中间的恒速段平直线加上两侧加速段和减速段多项式曲线构成的轨迹
  lspb函数Linear Segment(匀速) with Parabolic（抛物线） Blends（过渡）
  ①s=lspb(0,1,50)：值在0-1范围内分50个时间段
  ② [s,sd,sdd]=lspb(0,1,50)
  ③ s=lspb(0,1,50,0.025)：可以通过第四个输入参数为直线段指定一个速度

多维

将平滑的标量轨迹扩展为向量情况，可直接使用函数mtraj
得到一个50*2的矩阵x，每一行对应一个时间步，每一列对应一个轴，输入给mtraj，第一个参数是函数tpoly或lspyb，生成一个标量轨迹
eg:分50个时间步从（0,2）移动到（1，-1）可以表示为：

%x=mtraj(@tpoly,[0 2],[1 -1] ,50);
x=mtraj(@lspb,[0 2],[1 -1],50):
plot(x)
1
2
3

代码详解：
①mtraj：第一个参数是函数tpoly或lspyb

多段矩阵

mstraj可以基于中间点矩阵生成一个多段多轴轨迹，例如，有4个中间点的两轴运动可以用：

via = [4,1;4,4;5,2;2,5];
q = mstraj(via,[2,1],[],[4,1],0.05,0);		
plot(q,'*')
1
2
3

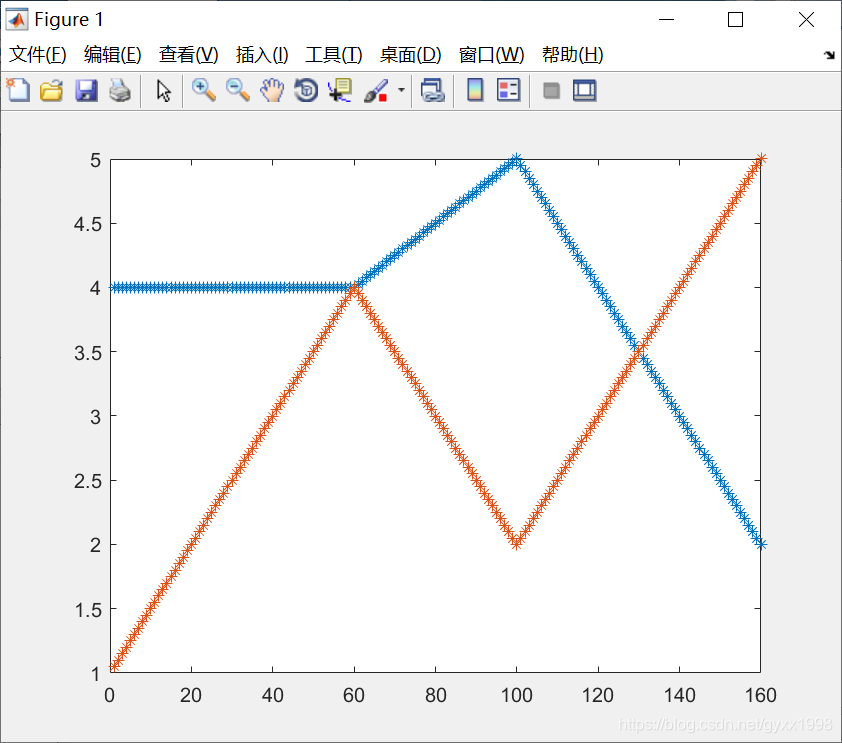
函数mstraj返回一个矩阵，行对应时间每步，列对应各个轴

可以增加加速时间，轨迹将会变得更加圆滑

q=mtraj(via,[2,1],[],[4,1],0.05,1);
plot(q,'*')
1
2

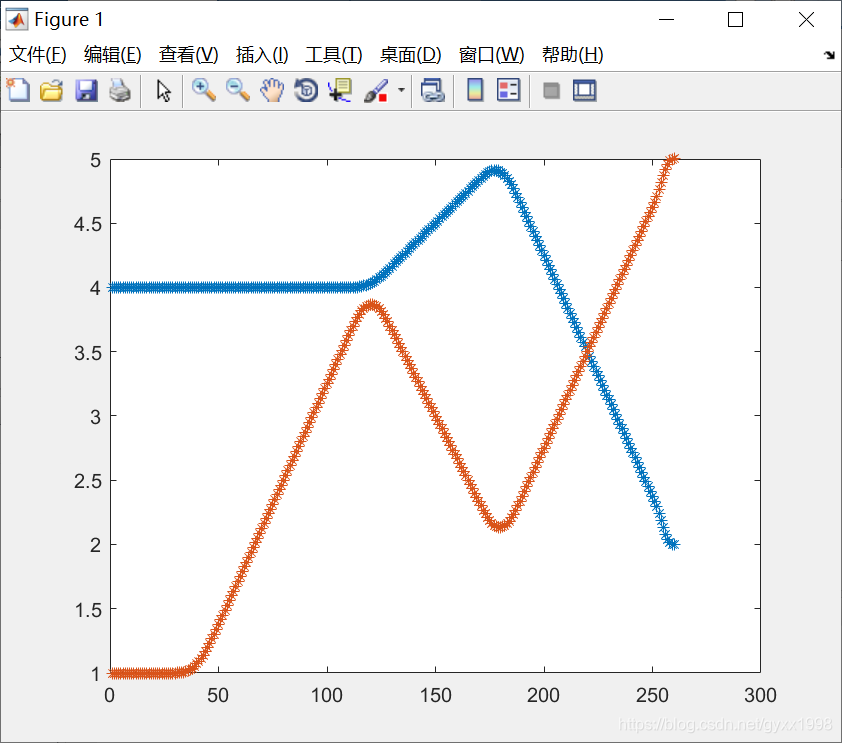
代码详解：
① q = mstraj(via,[2,1],[],[4,1],0.05,0);：函数mstraj返回一个矩阵，行对应时间每步，列对应各个轴

• 函数mstraj第1个参数：中间点矩阵，每点对应矩阵一行；
• 第2、第3个参数：每轴最大速度向量；每段运动时间向量；（设置一个，另一个为[ ]）
• 第4个参数：起点各轴坐标；
• 第5个参数：采样时间间隔；
• 第6个参数：加速度时间：增加加速时间，轨迹将会变得更加圆滑，eg：q=mtraj(via,[2,1],[],[4,1],0.05,1);