热门标签
热门文章
- 1Python提取高频词作为话题词_python词汇话题聚类
- 2软件测试人员如何筛选目标公司?_软件测试想找甲方在哪投简历呢
- 3下载vue.js devt-tool失败,解决方案_devtools下载地址打不开
- 4python实现简单的模拟发送短信验证码_python 伪发送验证码
- 5Hive默认分隔符介绍
- 6Android中获取手机的IMEI_getimei oncompletelistener
- 7Mac免费软件下载网站推荐(最全免费,替代MacWk)_mac软件下载网站推荐
- 8R3Live系列学习(一)Loam-Livox源码阅读_r3live livox
- 9还不快收藏起来!何恺明全网最全论文合集_何恺明resnet论文
- 10AI论文速读 |【Mambda×时序预测】 时光机(TimeMachine):A Time Series is Worth 4 Mambas for Long-term Forecasting_timemachine: a time series is worth 4 mambas for l
当前位置: article > 正文
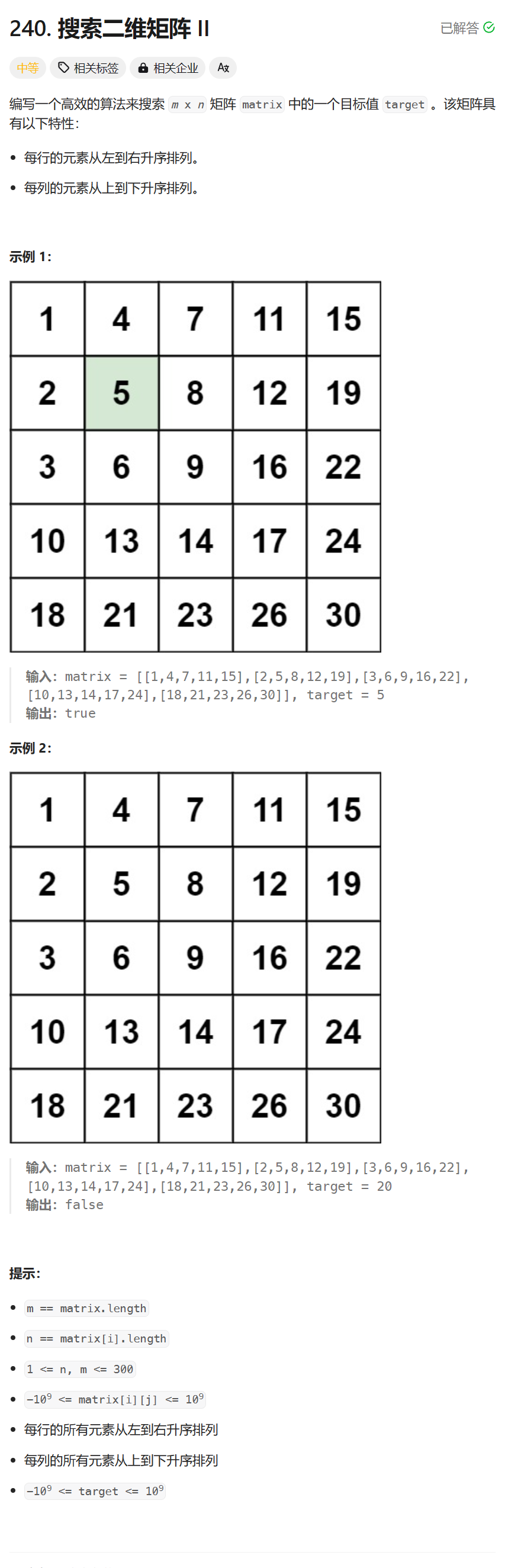
每日两题 / 240. 搜索二维矩阵 II && 48. 旋转图像 - 力扣(LeetCode热题100)
作者:繁依Fanyi0 | 2024-04-29 09:07:16
赞
踩
每日两题 / 240. 搜索二维矩阵 II && 48. 旋转图像 - 力扣(LeetCode热题100)
从右上角开始搜索,若当前值大于target,向左走,因为当前列的所有值都大于target
若当前值小于target,则当前行向左的所有值小于target,向下走
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size() - 1, n = matrix[0].size() - 1;
int x = 0, y = n;
while (x >= 0 && x <= m && y >= 0 && y <= n)
{
if (target == matrix[x][y]) return true;
else if (target < matrix[x][y]) y -- ;
else x ++ ;
}
return false;
}
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
48. 旋转图像 - 力扣(LeetCode)
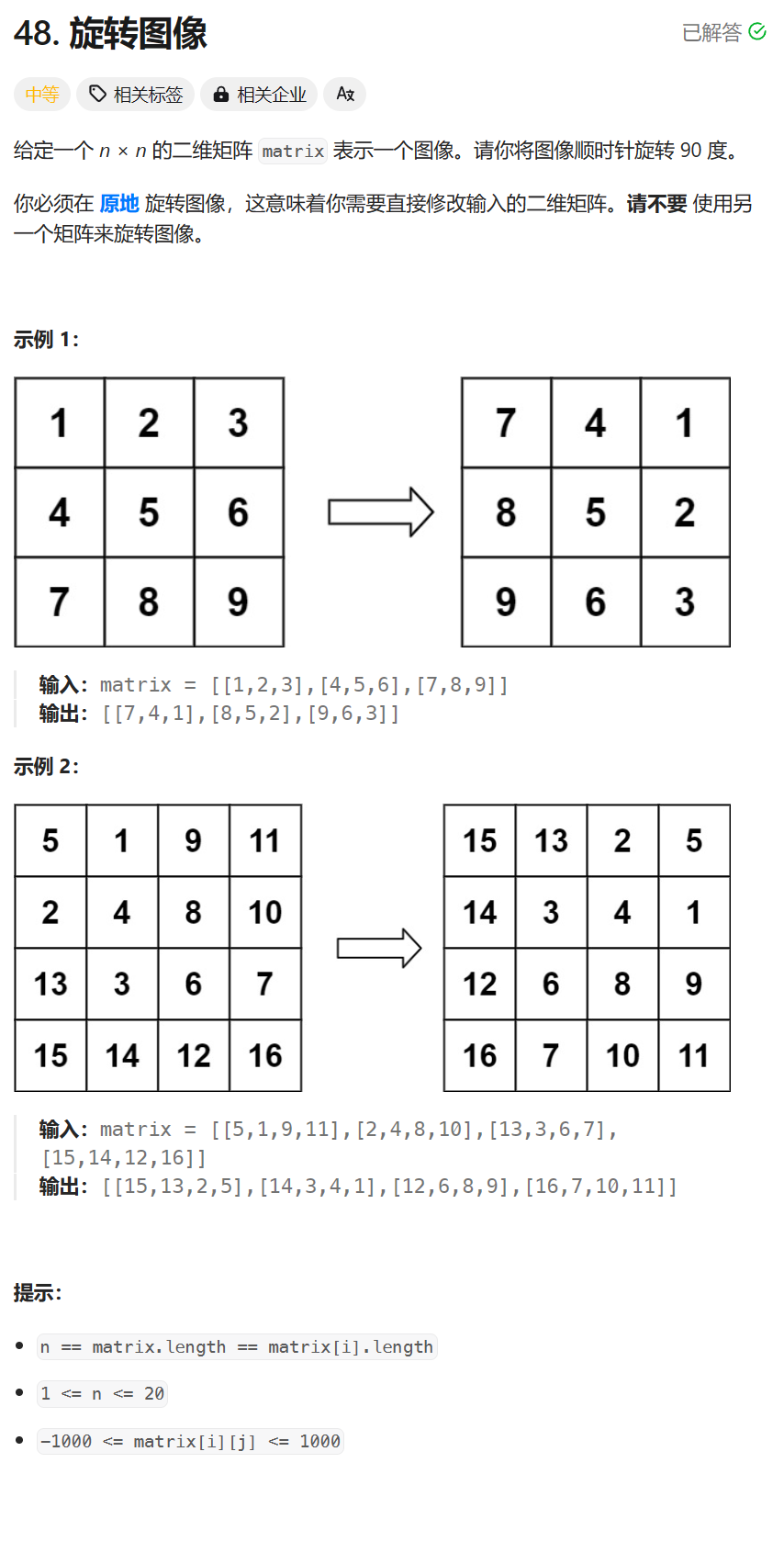
讲一个符合我直觉的解法:从外向内,一层层地旋转
每次完成一层中4个数的位置交换,如何得到这4个数的坐标?
每次坐标的变化,方向都是固定的:右下左上
并且每次的曼哈顿距离都是相同的
加上每次向一个方向移动k个曼哈顿距离,但是移动后的坐标“出界”,此时就要向另一个方向调整
将出界的曼哈顿距离加到另一个方向上
class Solution { public: void rotate(vector<vector<int>>& matrix) { int n = matrix.size(), m = matrix[0].size(); int dx[4] = { 0, 1, 0, -1 }, dy[4] = { 1, 0, -1, 0 }; int l = 0, r = m - 1, u = 0, d = n - 1; int len = m - 1; for (int i = 0; i < n / 2; ++ i) { for (int j = i; j < m - i - 1; ++ j) { int x = i, y = j; int next, cur = matrix[x][y]; for (int k = 0; k < 4; ++ k) { int nx = x + len * dx[k], ny = y + len * dy[k]; if (ny > r) { nx += (ny - r); ny = r; } else if (nx > d) { ny -= (nx - d); nx = d; } else if (ny < l) { nx -= (l - ny); ny = l; } else if (nx < u) { ny += (u - nx); nx = u; } x = nx, y = ny; next = matrix[nx][ny]; matrix[nx][ny] = cur; cur = next; } } l ++ , r --, u ++ , d -- ; len -= 2; } } }; // 右下左上 // j+, i+ // i+, j- // j-, i+ // i-, j+
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
本文内容由网友自发贡献,转载请注明出处:https://www.wpsshop.cn/w/繁依Fanyi0/article/detail/506965
推荐阅读
相关标签