LeetCode LCR 055.二叉搜索树迭代器

作者：菜鸟追梦旅行 | 2024-03-02 21:06:28

踩

实现一个二叉搜索树迭代器类BSTIterator ，表示一个按中序遍历二叉搜索树（BST）的迭代器：

BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字，且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字，则返回 true ；否则返回 false 。
int next()将指针向右移动，然后返回指针处的数字。
注意，指针初始化为一个不存在于 BST 中的数字，所以对 next() 的首次调用将返回 BST 中的最小元素。

可以假设 next() 调用总是有效的，也就是说，当调用 next() 时，BST 的中序遍历中至少存在一个下一个数字。

示例：
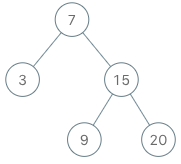
在这里插入图片描述

输入
inputs = [“BSTIterator”, “next”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”]
inputs = [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]

解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False

提示：

树中节点的数目在范围 [1, 105] 内
0 <= Node.val <= 106
最多调用 105 次 hasNext 和 next 操作

法一：在构造函数中递归计算出中序遍历的结果：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
public:
    BSTIterator(TreeNode* root) {
        inOrder(root);
    }
    
    int next() {
        return res[iterator++];
    }
    
    bool hasNext() {
        return iterator < res.size();
    }

private:
    vector<int> res;
    int iterator = 0;

    void inOrder(TreeNode *node)
    {
        if (node == nullptr)
        {
            return;
        }

        inOrder(node->left);
        res.push_back(node->val);
        inOrder(node->right);
    }
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * int param_1 = obj->next();
 * bool param_2 = obj->hasNext();
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

如果树中有n个节点，则此算法时间复杂度为O(n)，随后每次调用的时间复杂度为O(1)；空间复杂度为O(n)，因为要保存中序遍历的结果。

法二：迭代法，我们可以用栈模拟递归，每次调用next时再计算下一个遍历的结果：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
public:
    BSTIterator(TreeNode* root) { 
        cur = root;
    }
    
    int next() {
        while (cur)
        {
            s.push(cur);
            cur = cur->left;
        }

        cur = s.top();
        int res = cur->val;
        s.pop();
        cur = cur->right;

        return res;
    }
    
    bool hasNext() {
        return !s.empty() || (cur != nullptr);
    }

private:
    stack<TreeNode *> s;
    TreeNode *cur;
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * int param_1 = obj->next();
 * bool param_2 = obj->hasNext();
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

如果树中有n个节点，每次调用next的时间复杂度最差为O(n)（当树退化为链表时），均摊时间复杂度为O(1)；空间复杂度取决于树的高度，平均为O(logn)，最差为O(n)。

法三：morris遍历，核心要点是找到前驱节点，如中序遍历，需要找到当前遍历节点的前驱节点，即左节点的最右节点nodeLR，将nodeLR的右节点指向当前遍历到的节点本身：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
public:
    BSTIterator(TreeNode* root) {
        cur = root;
    }
    
    int next() {
        while (cur)
        {
            if (!cur->left)
            {
                break;
            }

            TreeNode *mostRightOfLeft = getMostRightOfLeft(cur);
            if (!mostRightOfLeft->right)
            {
                mostRightOfLeft->right = cur;
                cur = cur->left;
            }
            else if (mostRightOfLeft->right == cur)
            {
                mostRightOfLeft->right = nullptr;
                break;
            }
        }

        int res = cur->val;
        cur = cur->right;
        return res;
    }
    
    bool hasNext() {
        return cur;
    }

private:
    TreeNode *cur;

    TreeNode *getMostRightOfLeft(TreeNode *node)
    {
        TreeNode *tmpNode = node->left;
        // 当右节点为空，或右节点是输入节点时退出循环
        while (tmpNode->right && tmpNode->right != node)
        {
            tmpNode = tmpNode->right;
        }
        return tmpNode;
    }
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * int param_1 = obj->next();
 * bool param_2 = obj->hasNext();
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

此算法时间复杂度为O(1)，空间复杂度为O(1)。

法四：二叉搜索，中序遍历的结果是树中所有结点从小到大排列，因此每次都找比当前遍历到的值大的一个节点即可：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
public:
    BSTIterator(TreeNode* root) 
        : root(root),
          cur(nullptr) 
    { }
    
    int next() {
        // 首次运行，找最小值
        if (!cur)
        {
            cur = root;
            while (cur->left)
            {
                cur = cur->left;
            }
            return cur->val;
        }

        TreeNode *target = getTarget();
        cur = target;
        return target->val;
    }
    
    bool hasNext() {
        // 首次运行时，是否有下一个取决于是否是空树
        if (!cur)
        {
            return root;
        }

        // 如果有比当前值大的，就有下一个节点
        TreeNode *target = getTarget();
        return target;
    }

private:
    TreeNode *root;
    TreeNode *cur;

    TreeNode *getTarget()
    {
        TreeNode *node = root;
        TreeNode *res = nullptr;
        while (node)
        {
            // 找到比当前值大的一个最小节点
            if (node->val > cur->val)
            {
                res = node;
                node = node->left;
            }
            else
            {
                node = node->right;
            }
        }

        return res;
    }
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * int param_1 = obj->next();
 * bool param_2 = obj->hasNext();
 */
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

如果树有n个节点，此算法next和hasNext函数的时间复杂度为O(logn)，空间复杂度为O(1)。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/菜鸟追梦旅行/article/detail/182440