yolov7检测算法Loss总结_qfocal loss

        检测算法作为深度学习的一种主要基础算法，一直吸引着广大的科研工作者。这里总结了一些常见的Loss，作为记录。

目录

1.BCEBlurWithLogitsLoss

2.FocalLoss

 3.QFocalLoss

4.APLoss

5.aLRPLoss

6.RankSortLoss

7.IOULoss

GIoU

DIoU 

CIoU（Complete IoU loss）

Enhanced Completed IoU

Efficient IoU Loss

αIoU

SIoU

---

        检测算法一般包含分类损失(区分目标类别的)，回归损失（回归坐标的），目标置信度（表示是否存在目标的，也是一个分类损失）。先说分类损失：

1.BCEBlurWithLogitsLoss

        BCEBlurWithLogitsLoss是BCE函数的一个变种，在yolov5中提出来的，其目的是削弱missing样本(就是存在目标但是没有标注出来)带来的负面影响。其实就是通过降低missing样本loss的权重，降低其在反向传播中的比重，达到降低missing样本的负面影响的目的。但是笔者认为，这样可能导致模型无法区分目标和混淆目标，提高混淆目标的误检率。代码如下：

class BCEBlurWithLogitsLoss(nn.Module):
    # BCEwithLogitLoss() with reduced missing label effects.
    def __init__(self, alpha=0.05):
        super().__init__()
        self.loss_fcn = nn.BCEWithLogitsLoss(reduction='none')  # must be nn.BCEWithLogitsLoss()
        self.alpha = alpha
 
    def forward(self, pred, true):
        loss = self.loss_fcn(pred, true)
        pred = torch.sigmoid(pred)  # prob from logits
        dx = pred - true  # reduce only missing label effects
        # dx = (pred - true).abs()  # reduce missing label and false label effects
        alpha_factor = 1 - torch.exp((dx - 1) / (self.alpha + 1e-4))
        loss *= alpha_factor
        return loss.mean()

        其中，alpha_factor的函数曲线如下(alpha默认为0.05)

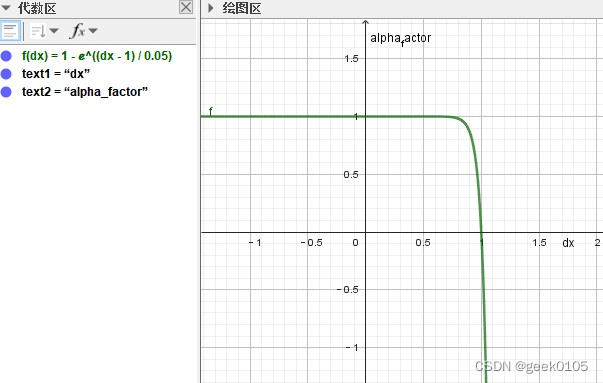
         横轴dx=pred-true，再没有使用label smooth的情况下，代表gt的true属于[0,1]，过完sigmoid的pred也属于[0-1].

        那么，missing的样本label即true为0，pred可能比较大，假如是0.9，alpha_factor接近0，该样本在反向传播中基本不起作用，达到了减少missing样本由于label错误导致的负面影响。但是，与此同时，与目标相似的混淆样本，label也为0，如果模型预测pred的分数也偏大，则该混淆样本的在反向传播中依然不起作用，则模型训练达不到区分混淆目标的目的。

        同理，代码中注释掉的  # dx = (pred - true).abs() 去除false样本（其实就是没有目标但是错误标注了一个目标）的负面影响。原理是，label=1，但是pred的分数较低，比如是0.1，0.1-1=-0.9，取绝对值就是0.9，对应的alpha_factor接近0，该样本在反向传播中几乎不起作用，达到了去除false样本的负面影响。但是，与此同时，外观形状变化比较大的目标可能会被误认为是false样本，在训练中不起作用，导致检测不到的问题。

        总之，这个loss有利有弊，只能根据数据集label的标注情况，结合alpha的参数调整，看情况是否适合使用。

2.FocalLoss

        FcoalLoss是何凯明大神在2017年发表的一篇论文：Focal Loss for Dense Object Detection.中提出的。

论文地址：https://arxiv.org/abs/1708.02002

        主要思路是: 通过增加困难样本的权重，让模型专注于困难样本（hard_sample）的学习，防止简单样本(easy_sample)过多主导训练的进程，可以解决难样本过少的问题。代码如下

 
class FocalLoss(nn.Module):
    # Wraps focal loss around existing loss_fcn(), i.e. criteria = FocalLoss(nn.BCEWithLogitsLoss(), gamma=1.5)
    def __init__(self, loss_fcn, gamma=1.5, alpha=0.25):
        super(FocalLoss, self).__init__()
        self.loss_fcn = loss_fcn  # must be nn.BCEWithLogitsLoss()
        self.gamma = gamma
        self.alpha = alpha
        self.reduction = loss_fcn.reduction
        self.loss_fcn.reduction = 'none'  # required to apply FL to each element
 
    def forward(self, pred, true):
        loss = self.loss_fcn(pred, true)
        # p_t = torch.exp(-loss)
        # loss *= self.alpha * (1.000001 - p_t) ** self.gamma  # non-zero power for gradient stability
 
        # TF implementation https://github.com/tensorflow/addons/blob/v0.7.1/tensorflow_addons/losses/focal_loss.py
        pred_prob = torch.sigmoid(pred)  # prob from logits
        p_t = true * pred_prob + (1 - true) * (1 - pred_prob)
        alpha_factor = true * self.alpha + (1 - true) * (1 - self.alpha)
        modulating_factor = (1.0 - p_t) ** self.gamma
        loss *= alpha_factor * modulating_factor
 
        if self.reduction == 'mean':
            return loss.mean()
        elif self.reduction == 'sum':
            return loss.sum()
        else:  # 'none'
            return loss

对于原始交叉熵

定义

可以简化为

         值得注意的是，简单样本在数据集中占据很大比重，并且简单样本的损失数值并不小，大量的简单样本会压倒困难样本，模型偏向于学到简单样本的信息。通常，通过引入一个系数来解决类别不均衡的问题

其中

由于，均衡交叉熵只能平衡正例和负例，不能平衡正样本和负样本。

所以，论文中对交叉熵引入了一个调制系数 ,叫做FocalLoss

函数的曲线如下：

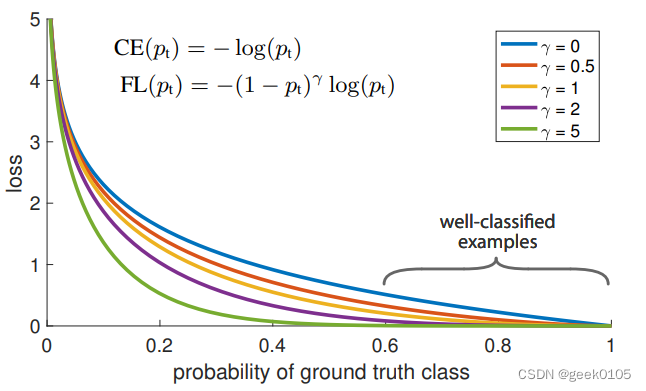
其实，就是对loss做了一个gama变换，使其在容易样本上快速降低，增加困难样本的比重，防止容易样本主导训练进程，从而达到难易样本均衡的问题。

另外，在实验中发现，alpha均衡对最终结果有一点提升，所以最终FocalLoss表达式如下：

默认gama取1.5，alpha取0.25.

 3.QFocalLoss

        QFocalLoss是2020年的一篇文章，主要是解决FocalLoss只能适用于标签是0-1这样的二分类或者多分类任务，对于使用了label smooth的任务则无法使用。QFL的公式如下：

QFL整理成FL的形式如下：

区别就在于调制系数，FocalLoss的调制系数是

QFocalLoss的调制系数是

代码如下：

 
class QFocalLoss(nn.Module):
    # Wraps Quality focal loss around existing loss_fcn(), i.e. criteria = FocalLoss(nn.BCEWithLogitsLoss(), gamma=1.5)
    def __init__(self, loss_fcn, gamma=1.5, alpha=0.25):
        super(QFocalLoss, self).__init__()
        self.loss_fcn = loss_fcn  # must be nn.BCEWithLogitsLoss()
        self.gamma = gamma
        self.alpha = alpha
        self.reduction = loss_fcn.reduction
        self.loss_fcn.reduction = 'none'  # required to apply FL to each element
 
    def forward(self, pred, true):
        loss = self.loss_fcn(pred, true)
 
        pred_prob = torch.sigmoid(pred)  # prob from logits
        alpha_factor = true * self.alpha + (1 - true) * (1 - self.alpha)
        modulating_factor = torch.abs(true - pred_prob) ** self.gamma
        loss *= alpha_factor * modulating_factor
 
        if self.reduction == 'mean':
            return loss.mean()
        elif self.reduction == 'sum':
            return loss.sum()
        else:  # 'none'
            return loss

4.APLoss

AP-Loss for Accurate One-Stage Object Detection

5.aLRPLoss

        基于Ranking的平均定位召回率(Average Localization Recall Precision)损失

论文 :A Ranking-based, Balanced Loss Function Unifying Classification and Localisation in Object Detection

6.RankSortLoss

Rank & Sort Loss for Object Detection and Instance Segmentation

秩和排序损失

7.IOULoss

IoU、GIoU、DIoU、CIoU、EIoU、αIoU、SIoU

IoU

IoU(Intersection over Union)交并比，是指目标框和预测框之间的交际除以并集. IoULoss广泛用于目标检测领域，并且发展出了诸多变体。

GIoU

针对不相交目标IoU都为0，GIoU引入了并集上的广义交集概念Generalized intersection over Union

• 论文：Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

其中C为目标框和预测框的最小外接矩形，对应的损失函数为

GIoULoss考虑了目标框和预测框无重叠区域造成的梯度消失问题，可以得到比 MSE 和 IoU 损失函数更高精度的预测框。

GIoU的问题：

1.预测框和目标框相互包含，GIoU退化为IoU

2.预测框和目标框宽高且处于同一水平或同一垂直线时，GIoU退化为IoU

DIoU 

论文：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

论文提出了预测框和目标框中心的距离作为损失的一部分，考虑了重叠面积+两框的距离，用于解决GIoU回归不准确和回归速度慢的问题

其中，c为最小外接矩形框的对角线欧氏距离，d为预测框和目标框中心点的欧氏距离。

因为DIoU Loss能够直接最小化两个boxes之间的距离，因此其收敛速度比IoU Loss与GIoU Loss更快。

CIoU（Complete IoU loss）

论文：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

CIoU也是DIoU这篇论文提出的

CIoU提出，一个优秀的回归定位损失应该考虑到3种几何参数：重叠面积、中心点距离、长宽比；

其中

CIoU 同时解决了收敛不准确和收敛速度慢的问题。同时考虑了长宽比。

• 当预测框和真值框距离较远时，权重变小，他们的长宽比相对来说重要程度变小，模型同时拉近预测框和真值框的中心点距离。
• 当预测框和真值框距离较近时，权重变大，长宽比重要程度变大，模型优化预测框和真值框的长宽比，模型依然还要拉近预测框和真值框的中心点距离。

与 GIoU 和 DIoU 一样，CIoU 也是通过迭代将预测框向真实框移动，但是 CIoU 所需要的迭代次数更少，并且得到的预测框与真实框的纵横比更为接近。

Enhanced Completed IoU

论文：Enhancing Geometric Factors in Model Learning and Inference for Object Detection and Instance Segmentation  https://arxiv.org/abs/2005.03572

CIoU的团队对CIoU做的改进，主要是改进了的值

Efficient IoU Loss

EIoU的主要贡献有两个，一个是将长宽比拆开，二是引入了Focal Loss解决难易样本不均衡的问题。

EIoU 在 CIoU 的基础上将长宽比拆开，明确地衡量了三个几何因素的差异，即重叠区域、中心点和边长，同时引入 Fcoal loss 解决了难易样本不平衡的问题。认为简单的任务框回归不需要用过大的权重来学习，而复杂的任务框回归需要大权重来学习，进而将 EIoU loss 进行改进提出 Focal EIoU loss 公式见下：

• 一般  设置为 0.5 即可。
• 当任务简单的时候，IoU 接近为 1，整体退化为 EIoU loss。
• 当任务困难的时候，IoU 值很小，而 EIoU 的值会变大。由于 IoU 的值小于 1，说明变换小于 EIoU Loss 变换。总体遇到难的任务时 loss 会增大，增加对难的回归样本的学习。

αIoU

论文：Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression 2110.13675.pdf (arxiv.org)

alphaIoU是IoU的大一统，对IoU和其他正则项增加一个幂系数

比如IoULoss:

'

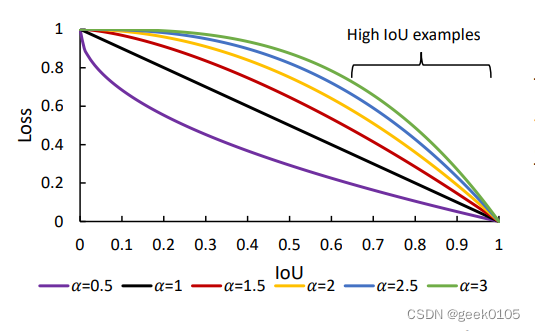
 其实类似Focal Loss，对IoU增加了一个gama变换，调整难易样本的比重。通过调整alpha的值，能够适应不同的数据集和训练精度，尤其是解决小样本带噪声数据。

类似的：

IoU显著优于现有的IoU-base的loss。

SIoU

论文：SIoU Loss: More Powerful Learning for Bounding Box Regression 

SIoU 提出了一种新的损失函数，重新定义了惩罚度量，考虑了期望回归之间的向量夹角。

传统的目标检测损失函数依赖于边界框回归指标的聚合，例如预测框和真实框（即 GIoU、CIoU 等）的距离、重叠区域和纵横比。然而，迄今为止提出和使用的方法都没有考虑期望的真实框和预测框之间不匹配的方向。这种不足导致收敛速度较慢且效率较低，因为预测框在训练过程中可能会“四处游荡”，最终会产生一个更差的模型。

参考：

(50条消息) 各种 IoU 损失变体_iou及其变体_有为少年的博客-CSDN博客