随机抽样一致(RANSAC)算法及matlab实现_matlab ransac

随机抽样一致(RANSAC)算法及matlab实现

一、算法介绍

RANSAC为RANdom SAmple Consensus（随机抽样一致）的缩写，它是根据一组包含异常数据的样本数据集，计算出数据的数学模型参数，得到有效样本数据的算法。它于1981年由Fischler和Bolles最先提出。

RANSAC算法的应用背景是在一堆观察点中估计出某个模型$y$。

以2D模型为例，RANSAC算法要估计 数据的最优模型$y=ax+b$ 。

二、算法步骤

Step1：随机抽取n个数据

从样本集合中取出n个数据。然后用这n个点去实例化模型，并将仿射变换计算出来。这个计算过程可以使用最小二乘法等等不限。需要注意的是，在选取n的时候，要随机选择最小数量的点以尽可能高的效率来检测可能的模型。例如如果模型是直线型，则$n=2$。

如果$n$超过了最小数量，会带来如下缺点：

1.计算复杂性增加。每次迭代需要选择和处理更多的点，这可能导致算法运行速度变慢。对于直线来说，任何两点都可以确定一条直线，所以选择超过两点会增加不必要的计算。

2.更容易受到异常值的影响。如果随机选择三个点，并且其中两个是异常值，那么通过这三个点确定的直线可能会受到异常值的严重影响。而如果你只选择两个点，异常值对结果的影响可能会减少。

3.可能会导致过拟合。如果数据集中有很多异常值，使用更多的点来确定模型可能会导致模型过于复杂，从而更容易拟合到这些异常值，这被称为过拟合。

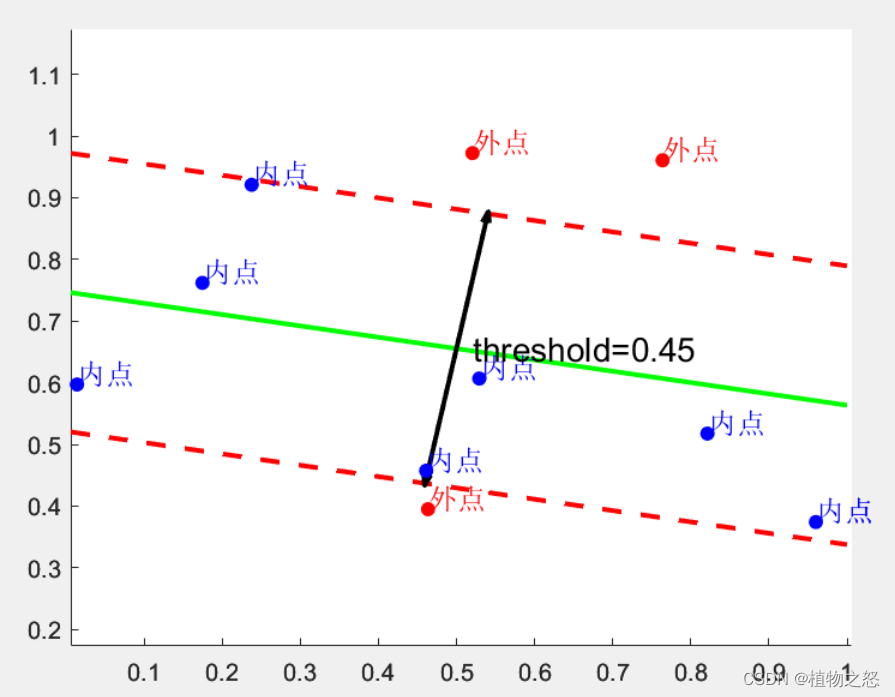
Step2：计算所有点到模型的距离d_i与距离门限(threshold)的距离t

定义内点*(inliers)和外点(outliers)*，其中内点可以被认为正确数据，即可以被模型描述的数据；外点可以被认为异常数据，即偏离正常范围很远、无法适应数学模型的数据。
{ ∣ d i ∣ < t , i = inlier; ∣ d i ∣ ≥ t , i = outlier; (1)

$$\begin{cases}|d_i| < t, \text{i = inlier;} \\ |d_i| ≥ t, \text{i = outlier;} \\ \end{cases}$$ \tag{1} {∣di​∣<t,i = inlier;∣di​∣≥t,i = outlier;​(1)

Step3：寻找最优模型

统计inliers的数量，记为S_i，定义数量门限为T。if S_i≥T，则认为此模型是合格的模型。即可以用这S_i个inliers去重新估计模型*(re-estimate the model)。if S_i < T，则重复Algorithm1-3，重新计算模型、求inliers和outliers*，直到得到合格的模型。

由于之前的model是由n个data所估计得到，而全部数据计算得到的inliers的数量S_i一定大于n。则此时所估计出的新模型的准确度一定高于之前用n个数据所估计的旧模型。

Step4：重复N次试验(repeat for N trials)

在N次重复试验中，每次会存在一个S_ij(1≤j≤N)。然后在此之中选择拥有最大的内点个数*S_imax*的模型，作为最优估计模型。

这里存在两个问题：

​ 1、如何判断两个门限t和T。t会影响内点个数，而T又会因环境不同而有不同取值。

​ 2、如何定义重复次数N。

三、距离门限t的选择

假设数据$X=[X_1,X_2]$服从方差为$\sigma$的高斯分布。则其到模型的距离之平方服从卡方分布(chi-square distribution)。
$$X_{1si}^2+X_{2si}^2=d_{si}^2\sim {\chi }^2(2)\text{\hspace{1em}(2)}$$
其中，$X_{1s}$和$X_{2s}$分别代表对数据$X$的标准化后得到的二维数据，$d_{si}$是标准化后的距离。定义标准化门限距离$t_s$，计算距离平方$d_{is}^2<t_s^2$的概率，此概率满足下式累积分布函数(CDF)：
$$F(x|k)=P(X\le x)=\frac{1}{\Gamma (\frac{m}{2})}{\int }_0^x{t}^{\frac{m}{2}-1}{e}^{-\frac{t}{2}}dt\text{\hspace{1em}(3)}$$
其中$\Gamma$是Gamma函数，$k$是卡方分布的自由度。这个CDF是卡方随机变量$X$小于或等于$x$值的概率。

此处下标$m$为卡方分布的自由度，数据$X$有几个维度，卡方分布就有几个自由度。当数据$X$存在于二维平面时，$m=2$。
{ d i s 2 < t s 2 , i = inlier; d i s 2 ≥ t s 2 , i = outlier; (4)

$$\begin{cases}d_{is}^2 < t_{s}^2, \text{i = inlier;} \\ d_{is}^2 ≥ t_{s}^2, \text{i = outlier;} \\ \end{cases}$$ \tag{4} {dis2​<ts2​,i = inlier;dis2​≥ts2​,i = outlier;​(4)
假设此时，距离小于门限值的概率，也即inliers出现的概率为$\alpha$，即 $P(d_i^2<t^2)=\alpha$，则：
$$t_s^2=F_k^{-1}(\alpha )\text{\hspace{1em}(5)}$$

$$t^2=F_k^{-1}(\alpha ){\sigma }^2\text{\hspace{1em}(6)}$$

四、数量门限T的选择

假设$ϵ$是在所有数据中取到一个outlier的概率，则取到一个inliers的概率为$(1-ϵ)$。

门限T控制着inliers的数量S_i。当每次取出$n_{total}$个数据时，理论上inliers的数量应为$n_{total}(1-ϵ)$。故而可以将这个数定义为数量门限T*。即，
$$T=n_{total}(1-ϵ)\text{\hspace{1em}(7)}$$

五、重复试验轮数N的选择

对于N的选择：由于在一般条件下，outlier的数量应该很少，$(1-ϵ)$的值应该接近于1。为了保证N次试验中，一定有一次试验可以满足门限T，则要保证在N次实验中，至少有一次，随机抽样的n个点都是inliers。

假设一次随机抽样得到inliers的概率是$w=1-ϵ$。

则n次随机抽样下，至少有1点是outlier的概率为$1-w^n$。

则N次重复试验中，每次抽样的点都至少有1个是outlier的概率为$(1-w^n{)}^N$。

则在N次重复试验中，至少有1次试验所抽取的点全都是inliers的概率为$P=1-(1-w^n{)}^N$。

实际处理中，可以假设一个接近于1的P，则有
$$N=lo{g}_{(1-w^n)}(1-P)\text{\hspace{1em}(8)}$$

六、外点出现概率$ϵ$的估计

上述几个参数的选择，或多或少都与outlier出现概率$ϵ$有关，但是在实际处理数据过程中，并不能预先知道数据中有多少个outlier。基于此，可以有两种方法来推动算法的继续。

1.假设$ϵ=0.5$，即取到最坏的情况。若outlier出现的概率大于0.5，则该数据质量过差，使用RANSAC算法来处理也将变得毫无意义。

2.直接取$N=\infty$，然后设定一个计数器$iteration=0$，如果$N>iterationt$，则进行循环。统计n个抽样点中inliers的个数，记为S_i，则此时，对outlier概率的估计为:
$$\widehat{ϵ}=1-\frac{S_i}{n}\text{\hspace{1em}(9)}$$
显然，由于此时的模型并不是最佳模型，所以求出的$\widehat{ϵ}$并不是最佳模型下outlier的概率。一般来说，此概率会大于实际outlier的概率。即$\widehat{ϵ}>ϵ$。

再将估计的概率带入公式(7)中，可以得到$N$的估计$\hat{N}$：
$$\hat{N}=lo{g}_{(1-(1-\widehat{ϵ}{)}^n)}(1-P)\text{\hspace{1em}(10)}$$
然后，再将计数器加一，重复循环。

N = inf;count=0;
if N > iteration
	calculate Si;
	epsilon_hat = 1-Si/n;
	calculate N_hat;
	N = N_hat;
	increment iteration by 1;
end
1
2
3
4
5
6
7
8

七、代码实现与结果分析

如前所述，在2D条件下，可以有如下步骤：

1. 数据生成和初始化：

clear, clc, close all
% 生成合成数据
x = 1:200;
sigma = 10;mu = 0;
y_true = 2*x + 5;
y = 2*x + 5 + mu + sigma*randn(1,length(x)); % 加入标准差为sigma的高斯噪声

% 添加较大的误差点
num_out = 7;
sigma_out = 100;
idx = randperm(length(x), num_out);
y(idx) = y(idx) + sigma_out*rand(1);
data = [x', y'];
1
2
3
4
5
6
7
8
9
10
11
12
13

设置200个点，理论模型为$y=2x+5$，给他们添加均值为0，标准差为10的高斯噪声。这个高斯噪声视为测量数据的随机误差。

此外，再随机抽取7个点，给他们添加均值为0，标准差为100的高斯噪声。这个高斯噪声视为设置较大的测量野值，野值比随机误差的标准差要高出一个量级。

2. 门限值$t$的设置：

假设此时，认为测量数据中，outliers只占0.5%。根据自由度为2的卡方分布的逆累积分布函数，根据给定的置信度P_t计算门限值(threshold)。

% 设置门限值
Pt = 0.995;  % Pt设为0.995
% 使用chi2inv函数计算x值，自由度为2
threshold = sqrt(chi2inv(Pt, 2) * sigma);
1
2
3
4

3. 应用RANSAC算法：

调用编写好的ransacLineFit，对数据集的模型进行估计，并设置数量门限$T=0.95\ast n_{total}$。如果预测的最佳模型中包含的内点不足数据集总数的95%，则重新进行抽样，直到满足门限。即找到最佳拟合直线，并将结果进行可视化。

%% 应用RANSAC
k = 0;j=0;
while 1
    k=k+1;
    maxIter = inf;
    [bestLine, inlierIdx, j] = ransacLineFit(data, threshold, maxIter,j);
    T = length(data) * 0.965;
    if length(inlierIdx) >= T
        % 绘制结果
        figure;
        plot(data(:,1), data(:,2), 'ro', 'LineWidth', 1.8); hold on;   % 外点
        plot(data(inlierIdx,1), data(inlierIdx,2), 'go', 'LineWidth', 1.8);  % 内点
        plot(x, bestLine(1)*x + bestLine(2), 'b-', 'LineWidth', 2);       % RANSAC拟合的线
        plot(x, y_true, 'm-', 'LineWidth', 2)
        legend({'外点', '内点', 'RANSAC拟合的线', '理论值'}, 'Location','northwest', 'FontSize', 15);
        title('RANSAC算法对含噪声2维模型的估计', 'FontSize', 15);
        grid on
        P = length(inlierIdx) / length(data);
        fprintf(' 数量循环次数: %d, 算法迭代次数: %d\n', k, j);
        fprintf(' 预测模型的内点比例: %.2f%%\n', P*100);
        break
    end
end

% 使用一次多项式进行线性拟合
p = polyfit(data(:,1), data(:,2), 1);
y_fit = polyval(p, x);
% p(1) 是斜率，p(2) 是y轴截距。
hold on;
plot(x, y_fit, 'y-', 'LineWidth', 2);  % 拟合的线
legend({'外点', '内点', 'RANSAC拟合的线', '理论值', '直接线性拟合的模型'}, 'Location','northwest', 'FontSize', 15);
xlabel('x');
ylabel('y');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

4. 准确性评估：

对经过RANSAC算法估计出的模型进行准确性评估，包含绝对准确性和相对准确性。

1. 绝对准确性：考虑RANSAC拟合的直线与原始无噪声数据（y_true）之间的差异。
2. 相对准确性：首先使用所有被认为是内点的数据拟合一条直线，然后与RANSAC的结果进行比较。

%% 准确性评估
% 真实的线性模型参数
a_true = 2; b_true = 5;
% 计算RANSAC得到的线参数与真实值之间的误差
error_a = abs(bestLine(1) - a_true);
error_b = abs(bestLine(2) - b_true);
% 输出误差
disp('——————————————准确性评估——————————————')
fprintf(' 参数a误差: %f, 参数b误差: %f\n', error_a, error_b);
% 1. 绝对准确性评估
% 计算RANSAC拟合线与y_true之间的差异
y_ransac = bestLine(1)*x + bestLine(2);
abs_diff = y_ransac - y_true;
abs_mean_error = mean(abs(abs_diff));
fprintf('平均绝对误差: %f\n', abs_mean_error);

% 2. 相对准确性评估
% 使用所有内点重新拟合一条直线
inlier_data = data(inlierIdx, :);
P = polyfit(inlier_data(:,1), inlier_data(:,2), 1);  % 使用一次多项式拟合
y_inlier_fit = P(1)*x + P(2);

rel_diff = y_ransac - y_inlier_fit;
rel_mean_error = mean(abs(rel_diff));
fprintf('平均相对误差: %f\n', rel_mean_error);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

5. 鲁棒性评估：

计算RANSAC算法正确检测到的inliers的比例。并考虑使用不同比例的outliers进行测试，看看算法在何时开始失效或准确性下降。

%% 鲁棒性评估
% 通过改变离群点百分比来测试RANSAC的鲁棒性
disp('——————————————鲁棒性评估——————————————')
for outlierPercentage = 0.1:0.1:0.9
    % 计算给定百分比的离群点数量
    numOutliers = floor(outlierPercentage * length(x));
    % 在原始数据中添加随机离群点
    y_with_outliers = y;
    idx = randperm(length(x), numOutliers);
    y_with_outliers(idx) = y(idx) + 50*rand(1, numOutliers);
    data_with_outliers = [x', y_with_outliers'];
    % 使用RANSAC估计线性模型参数
    [bestLine, ~, ~] = ransacLineFit(data_with_outliers, threshold, maxIter, 0);
    % 计算估计参数与真实值之间的误差
    error_a = abs(bestLine(1) - a_true);
    error_b = abs(bestLine(2) - b_true);
    % 输出离群点百分比及对应的误差
    fprintf('外点比例: %f, 参数a误差: %f,  参数b误差: %f\n', outlierPercentage, error_a, error_b);
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

6. 效率评估：

对于不同大小的数据集或不同比例的离群点，记录RANSAC的运行时间。这有助于了解算法的效率和在大数据集上的可伸缩性。

%% 效率评估
% 计时RANSAC的执行时间
tic;
[bestLine, inlierIdx, ~] = ransacLineFit(data, threshold, maxIter, 0);
time_elapsed = toc;

% 输出RANSAC的执行时间
fprintf('代码执行时间: %f s\n', time_elapsed);
1
2
3
4
5
6
7
8

在本例中，数据量并不大，而且数据维度也不高，所以时间消耗并不大。

7. RANSAC线性拟合函数：

这是一个RANSAC的核心函数，用于从给定的数据中找到最佳的线性拟合。它随机选择数据点，用它们拟合直线，并计算数据点到该线的距离，然后基于门限值确定内点。这个函数重复进行，直到达到预定的迭代次数或者找到足够多的内点。

本例选取的重复试验轮数N由（10）式确定。

%% RANSAC线性拟合函数
function [bestLine, inlierIdx, j] = ransacLineFit(data, threshold, maxIter,j)
% data: Nx2矩阵，每行是一个数据点 (x, y)
% threshold: 距离阈值，用于确定内点
% maxIter: 最大迭代次数
% bestLine: 估计的线参数 [a b]，对应 y = ax + b
% inlierIdx: 内点在数据中的索引
numPoints = size(data, 1);
bestInCount = 0;
bestLine = [0 0];
inlierIdx = [];
currentMaxIter = maxIter;           % 当前的最大迭代次数
% 在函数开始部分初始化变量
iteration = 0;
while iteration < currentMaxIter
    j=j+1;
    % 随机选择2个点
    idx = randperm(numPoints, 2);
    sample = data(idx, :);
    % 使用这2个点拟合一条线
    a = (sample(2,2) - sample(1,2)) / (sample(2,1) - sample(1,1));
    b = sample(1,2) - a*sample(1,1);
    % 计算所有点到这条线的距离
    distances = abs(a*data(:,1) - data(:,2) + b) / sqrt(a^2 + 1);
    % 找到内点
    inliers = distances < threshold;
    % 如果当前模型比之前的好，则更新最佳模型
    numInliers = sum(inliers);
    if numInliers > bestInCount
        bestInCount = numInliers;
        bestLine = [a b];
        inlierIdx = find(inliers);
        % 根据内点比例动态更新currentMaxIter
        w = bestInCount / numPoints;
        p = 0.997;
        maxIterNew = ceil(log(1-p) / log(1-w^2));
        if w > 0.999
            % 设置一个迭代的上限，例如1e3
            currentMaxIter = min([maxIter, maxIterNew, 1e3]);
        else
            currentMaxIter = min(maxIter, maxIterNew);
        end
    end
    % 更新迭代次数
    iteration = iteration + 1;
end
end
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

8.结果分析

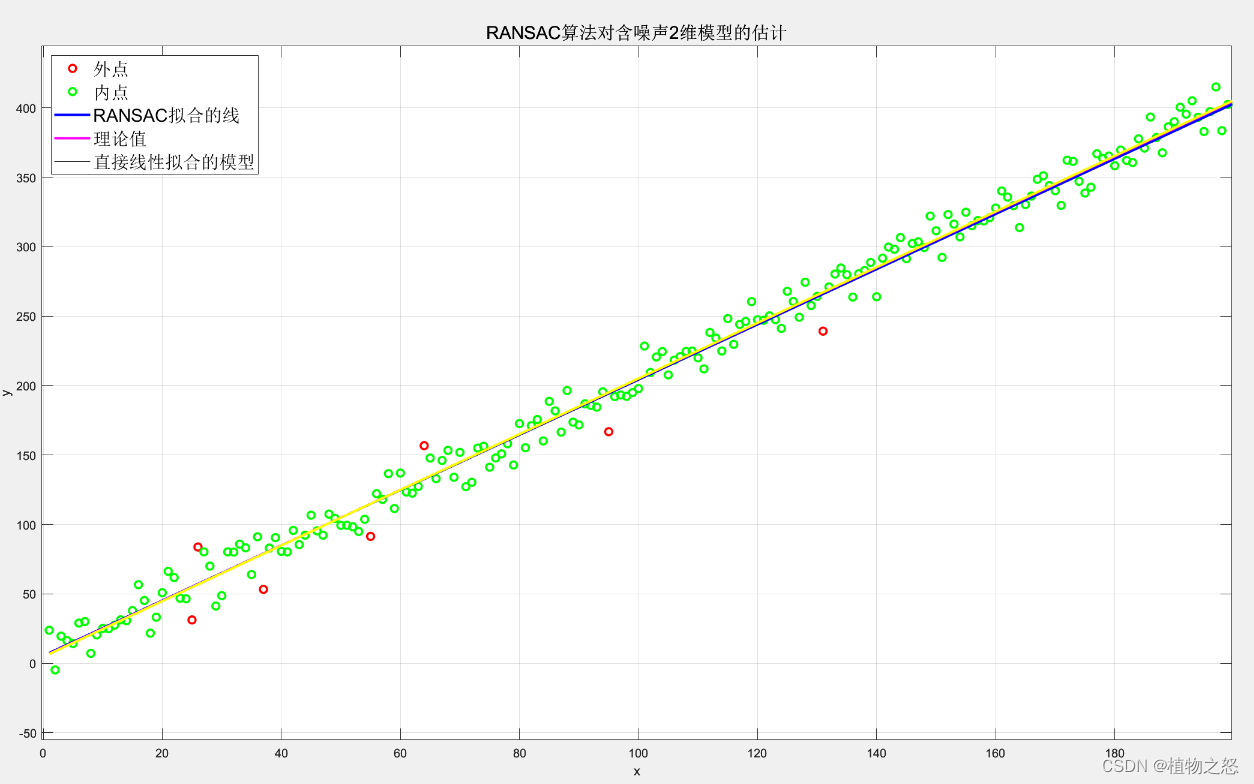
如上图，外点为红色，内点为绿色。粉线表示理论模型$y=2x+5$，蓝线表示在增加了随机噪声和测量野值后，经过RANSAC算法预测后的模型，黄线表示直接进行线性拟合的模型。

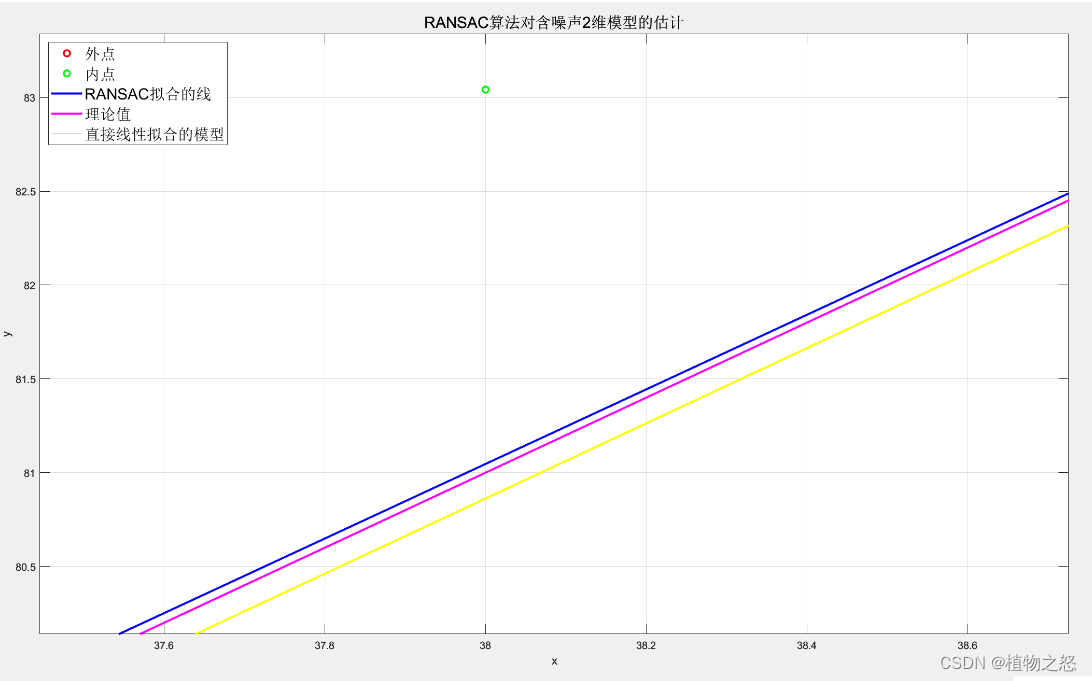
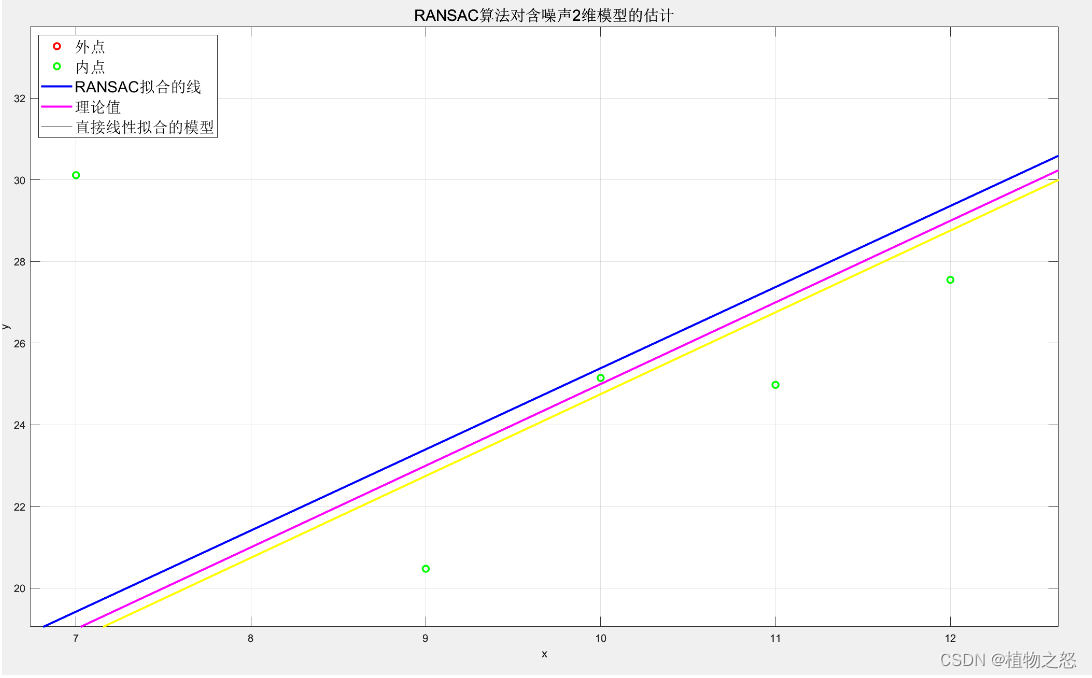
可以看到在局部区域二者性能相仿，在噪点较多的地方，RANSAC算法处理的模型要稍微优于直接拟合。

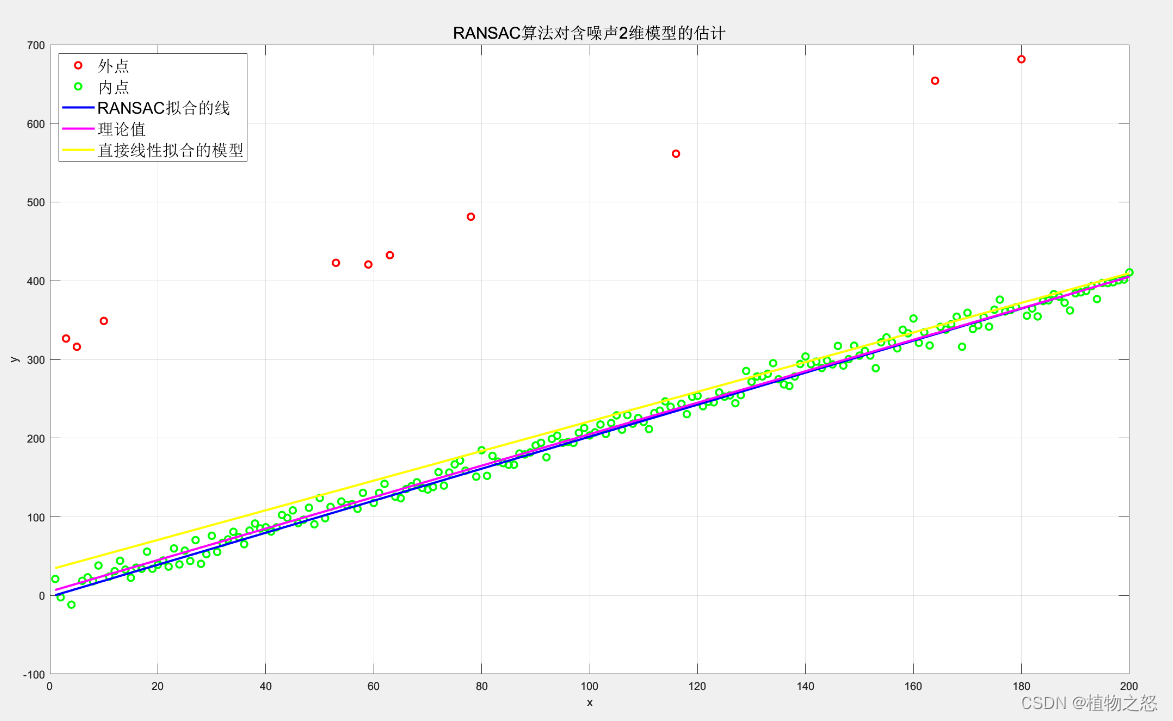
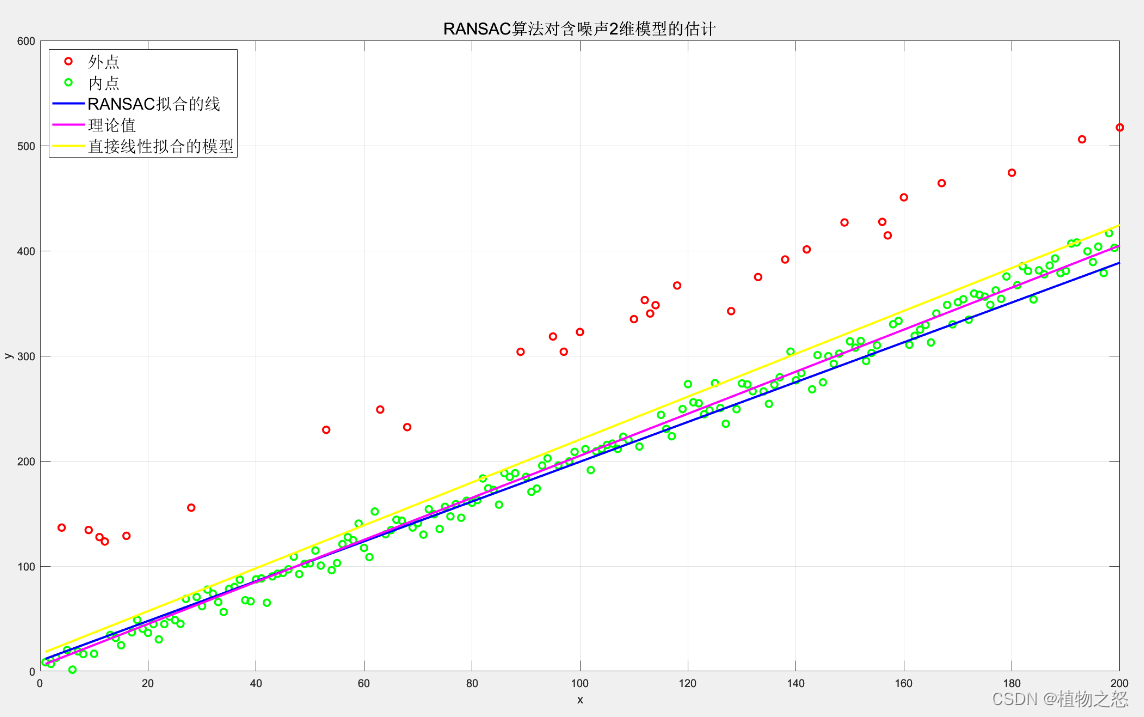
如上图所示，当野值偏差较大或数量较多时，RANSAC的性能显著优于直接线性拟合。

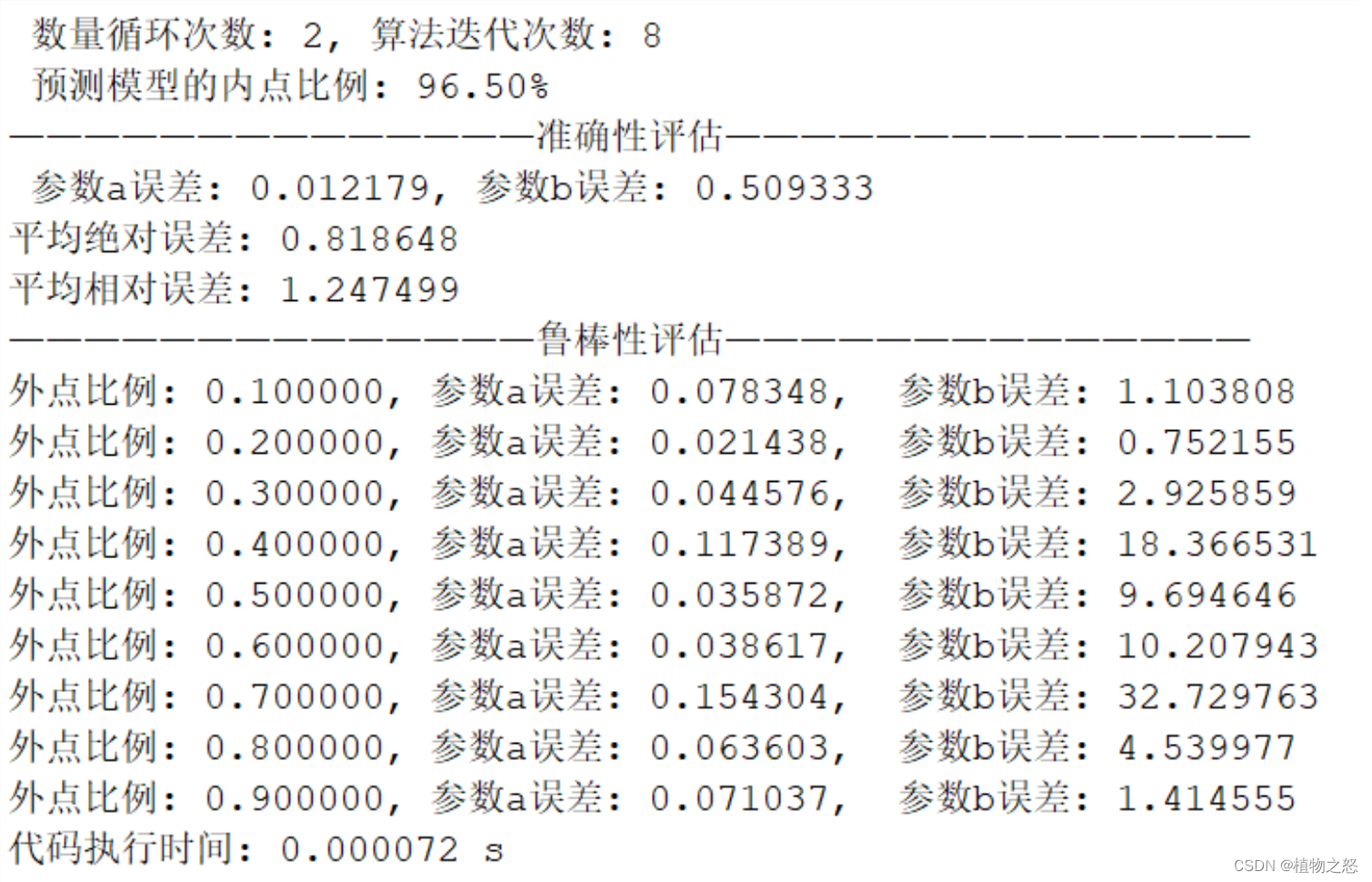
在本次的处理中，准确性较好。迭代次数也并不大，避免了大量的时间消耗。

对算法鲁棒性的分析中，可以看到从外点比例达到40%开始，算法的准确度就开始明显下降。同时，当外点比例达到80%以上时，由于本例采用高斯分布来仿真测量中的随机误差和测量野值，这使得当外点比例过大时，算法会将外点当作内点。由于外点和内点都符合高斯分布，所以也可以得到较好的“准确性”。但是在现实处理中，测量野值并不会服从什么分布，这就会使的当外点数量过大的时候，算法性能又进一步下降。