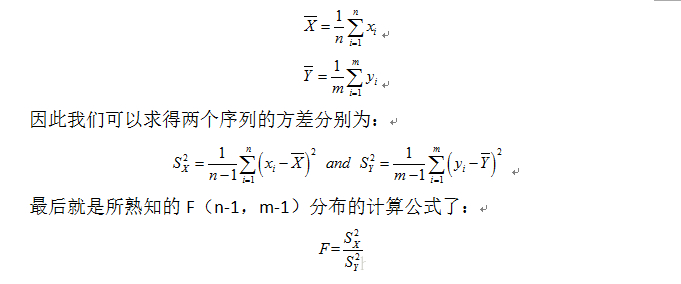假设检验方法-T检验、Z检验、F检验、卡方检验_t检验z检验f检验卡方检验区别

假设检验问题是统计推断中的一类重要问题，小编在之前给大家整理，分享过假设检验的基本步骤，今天给大家带来的是常见的假设检验方法，希望对大家有所帮助。

一、假设检验基本概念

假设检验是用来判断样本与样本之间，以及样本与总体之间的差异，是由抽样误差引起的，还是本质差别造成的一种方法。其基本原理是先对总体的特征作出某种假设，然后通过抽样研究的统计推理，对此假设应该被拒绝还是接受作出推断。

其基本思想为小概率反证法思想。小概率思想认为小概率事件在一次试验中基本上不可能发生，在这种方法下，我们先对总体的特征作出某种假设，这一假设大概率能够成立，但假如在一次试验中，试验结果与原假设相背离，也就代表着小概率事件发生了，那我们就有理由对原假设的真实性产生怀疑，从而拒绝这一假设。如果并没有与原假设相背离的实验结果出现，那么久不能拒绝原假设，从而需要接受原假设。

在假设检验中小概率常记为α，称为显著性水平。原假设，记作H0.与H0相反的假设叫做备择假设，代表着原假设被拒绝时而应接受的假设，记作H1.

二、常见的假设检验方法

1.T检验

又叫做student t检验，即Student's t test，通常用于样本含量较小(一般n<30)，总体标准差σ未知的正态分布。目的为：比较样本均数所代表的未知总体均数μ和已知总体均数μ0.

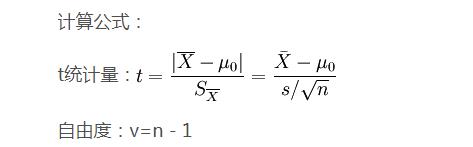
1)若要评断一个总体中的小样本平均数与总体平均值之间的差异程度，其统计量T值的计算公式为：

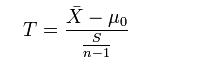
2)若要评断两组样本平均数之间的差异程度，其统计量T值的计算公式为：

T检验适用条件：

(1) 已知一个总体均数;

(2)能够得到一个样本均数及该样本标准差;

(3) 样本是来自正态或者是近似正态总体。

2.U检验(Z检验)

Z检验是通常用于大样本(也就是样本容量>30)平均值差异性检验的方法。是用标准正态分布的理论来推断差异发生的概率，从而对两个平均数的差异进行比较，判断该差异是否显著。

Z检验步骤：

（1）建立假设 H0:μ1 = μ2 ，也就是先假定两个平均数之间没有显著差异。

(2)比较样本均值和总体均值

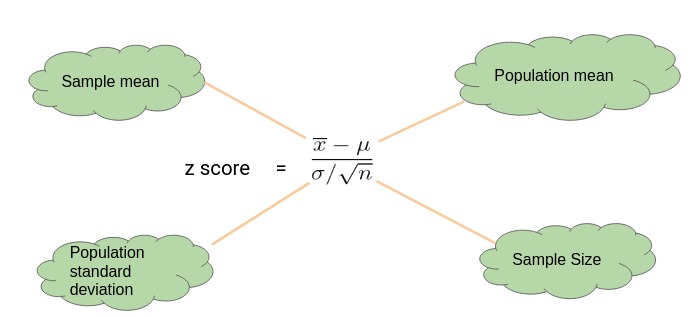
比较两个样本的平均值

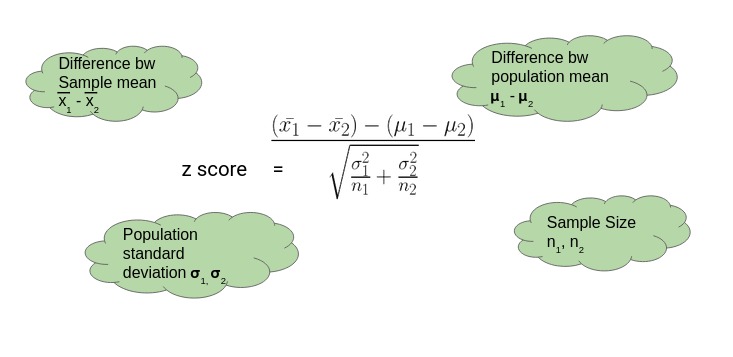
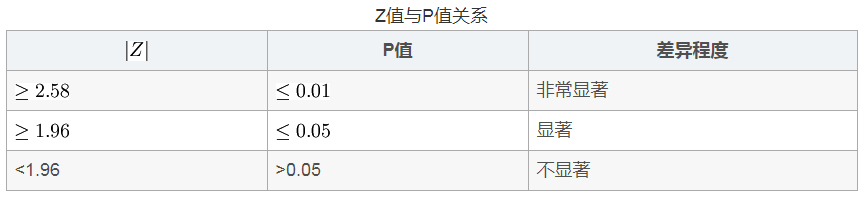
(3)对计算所得Z值与理论Z值进行比较，推断发生的概率，依据Z值与差异显著性关系表作出判断。

3.卡方检验

卡方检验又叫做X2检验，简单来说就是，检验两个变量之间有没有关系。

卡方检验属于非参数检验，通常是用来比较两个及两个以上样本率(构成比)，以及两个分类变量的关联性分析。基本思想为：比较理论频数和实际频数的吻合程度或者拟合优度问题。

X2计算公式为：

4.F 检验

F 检验是为检验方差是否有显著性差异。经常被叫做，联合假设检验(joint hypotheses test)，也可以叫做方差比率检验、方差齐性检验。

F 检验为一种在零假设(null hypothesis, H0)情况之下，统计值服从F-分布的检验。

F 检验计算公式