C语言实现数据结构：二叉树_以二叉链表创建二叉树 输出二叉树的中序结果的算法步骤

第二次上机实验报告

作业题目1：

实现以下算法：

1.以二叉链表表示二叉树，根据输入建立一棵二叉树；

2.输出二叉树的先序遍历结果；

3.输出二叉树的中序遍历结果；

4.输出二叉树的后序遍历结果。

程序运行结果截图，需测试各种情况。写出测试过程中遇到的主要问题及所采用的解决措施。

运行结果截图:

 

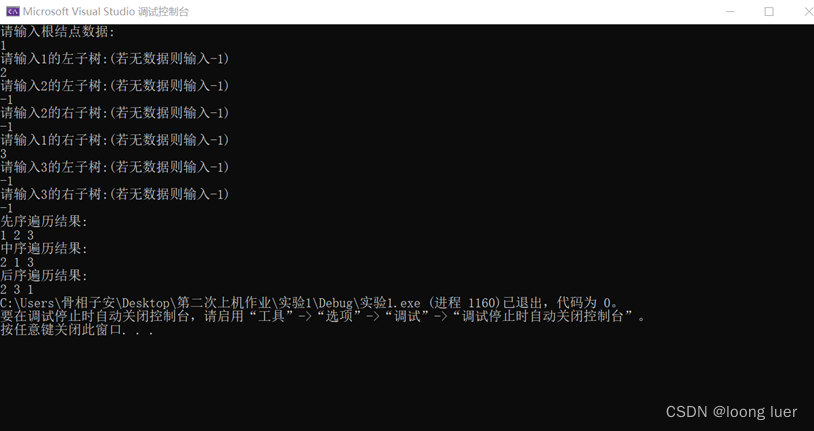
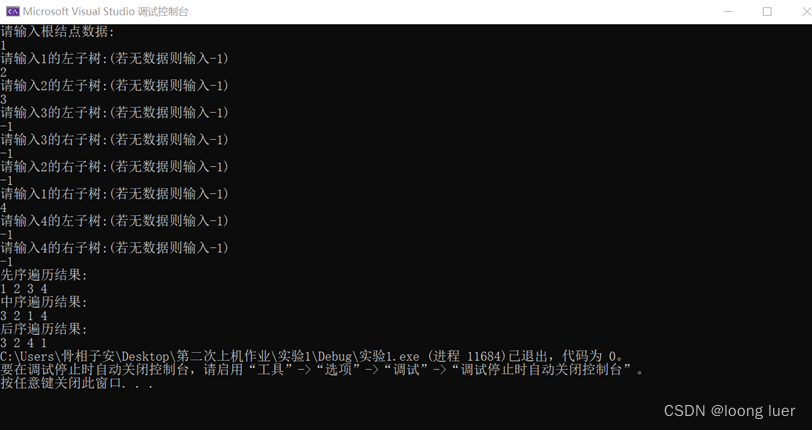
主要问题：创建树和输入树时顺序不好控制

解决办法：按树形输入，如果没有数据则输入-1，来提示输入已经结束了

代码:

BiTree.h

#pragma once
#include"function.h"
 
typedef struct Tree {
 
	int data;					    //	数据域
	struct Tree* lchild;			//	左子树指针
	struct Tree* rchild;			//	右子树指针
 
}Tree, * BiTree;
 
BiTree CreateBiTree();
void PreOrderTraverse(BiTree T);
void InOrderTraverse(BiTree T);
void PostOrderTraverse(BiTree T);

function.h

#pragma once
#include<stdio.h>
#include<stdlib.h>

function.cpp

#include"BiTree.h"
 
BiTree CreateBiTree()
{
	int data;
	int temp;
	BiTree T;
 
	scanf("%d", &data);		
	temp = getchar();			//	必须吸收一个后面的空格
 
	if (data == -1) {			//	输入-1 代表此节点下子树不存数据，不继续递归创建
 
		return NULL;
 
	}
	else {
		T = (BiTree)malloc(sizeof(Tree));		
		T->data = data;								           //把当前输入的数据存入当前节点指针的数据域中
 
		printf("请输入%d的左子树:(若无数据则输入-1)\n", data);
		T->lchild = CreateBiTree();					           //递归创建左子树
		printf("请输入%d的右子树:(若无数据则输入-1)\n", data);
		T->rchild = CreateBiTree();					           //开始到上一级节点的右边递归创建左右子树
		return T;							                   //返回根节点
	}
 
}
 
void PreOrderTraverse(BiTree T)			//先序遍历二叉树
{
	if (T == NULL)						
	{
		return;
	}
	printf("%d ", T->data);
	PreOrderTraverse(T->lchild);			
	PreOrderTraverse(T->rchild);			
}
 
void InOrderTraverse(BiTree T)			//中序遍历二叉树
{
	if (T == NULL)						
	{
		return;
	}
 
	InOrderTraverse(T->lchild);			
	printf("%d ", T->data);
	InOrderTraverse(T->rchild);			
 
}
//	后序遍历
void PostOrderTraverse(BiTree T)			//后序遍历二叉树
{
	if (T == NULL)						
	{
		return;
	}
 
	PostOrderTraverse(T->lchild);			
	PostOrderTraverse(T->rchild);			
	printf("%d ", T->data);
}

main.cpp

#include"BiTree.h"
 
int main()
{
	BiTree S;
	printf("请输入根结点数据:\n");
	S = CreateBiTree();			
	printf("先序遍历结果: \n");
	PreOrderTraverse(S);				
 
	printf("\n中序遍历结果: \n");
	InOrderTraverse(S);				
 
	printf("\n后序遍历结果: \n");
	PostOrderTraverse(S);				
 
	return 0;
}

作业题目2：求二叉树第k层结点的个数

求二叉树第k层结点的个数。

程序运行结果截图，需测试各种情况。写出测试过程中遇到的主要问题及所采用的解决措施。

运行结果截图:

主要问题：输入树和查找层数的顺序易错

解决办法：先输入非空结点的个数，这样有助于树的建立

代码:

BiTree.h

#include<iostream>
#include<cstdio>
#include<cstdlib>
 
using namespace std;
 
int sum = 0;
int K, L;
 
typedef struct binode
{
	int data;
	struct binode* lchild, * rchild;
}Binode, * Bitree;
 
void btinsert(Bitree& T, int i, int j, int d);
void traversal(Bitree T, int l);

main.cpp

#include"BiTree.h"
 
int main()
{
 
	Bitree h = NULL;
	printf("二叉树中非空结点的个数:\n");
	scanf("%d", &K);
	printf("要查找的层数k:\n");
	scanf("%d", &L);
	printf("按照顺序输入二叉树的多个结点值 (包含空结点，结点值之间用空格隔开):\n");
	for (int i = 1; K > 0; i++)
	{
		int d;
		
		scanf("%d", &d);
		if (d) K--;
		btinsert(h, i, 1, d);
	}
	traversal(h, 1);
	printf("二叉树第k层的结点个数为：%d\n", sum);
	return 0;
}
 
void btinsert(Bitree& T, int i, int j, int d)
{
	if (!d) return;
	if (i == j)
	{
		T = (Bitree)malloc(sizeof(Binode));
		T->data = d;
		T->lchild = T->rchild = NULL;
	}
	else
	{
		int t = i;
		while (t != j * 2 && t != j * 2 + 1)
		{
			t /= 2;
		}
		if (t == j * 2)
		{
			btinsert(T->lchild, i, j * 2, d);
		}
		else
		{
			btinsert(T->rchild, i, j * 2 + 1, d);
		}
	}
}
 
void traversal(Bitree T, int l)
{
	if (T == NULL) return;
	if (l == L) sum++;
	traversal(T->lchild, l + 1);
	traversal(T->rchild, l + 1);
}

作业题目3：

1.题目描述：

利用二叉树计算表达式的值。建立表达式树，并计算表达式的值。

2.问题分析：

1.程序的功能要求；

利用二叉树这一数据结构，建立树并且计算表达式求值

2.程序的界面设计：

第一行显示：“请输入表达式:”，然后自行输入表达式

第二行显示：“你输入的表达式为:……”

第三行显示：“Your result is ……”，显示计算结果

3.程序的错误处理：当输入非法数据时，直接结束程序

1.数据类型设计：

typedef struct  TNode {

 int flag;

 int data;//flag=0

 char ch;//flag=1

 struct TNode* lChild;//左孩子

 struct  TNode* rChild;//右孩子

};

2.算法设计（算法的基本思想、具体步骤，各程序模块之间的层次（调用）关系流程图等）：

在输入时，先把输入的结果存在一个数组中，然后用二叉树保存；遍历树，当发现为+、—、*、/四种符号时，则让树的左孩子、右孩子进行相应的操作，并把结果返回上一级字树的根。递归实现以上步骤，最终返回的根数据则为表达式的值。

3.测试分析

设计测试范例（测试数据包括正确的输入、边界条件、含有错误的输入等），列出程序的测试结果（附截图），测试结果的分析与讨论。可列出测试过程中遇到的主要问题及所采用的解决措施。

 4.心得

对实验设计与实现过程的回顾和分析，说明程序的改进思想、经验和体会。

对树这种类型的数据结构，一般尽量使用递归定义，这样可以简化运算，使其更高效。

在进行更大型的程序设计时，一般混用多个数据结构，比如栈、队列等，但要注意防止混淆。

5.附录

列出程序文件清单，及文件功能。

头文件：

count.h:存放头文件、基本数据结构、函数声明

源文件：

main.cpp:存放主函数和其他函数的文件

代码注释要求：

1. 对关键的算法实现代码有必要的注释
2. 函数说明格式：

*****************************************************

函数名：

函数功能：

输入参数：

       类型，参数名，含义

输出参数：

文件提交要求：

将两道题目各自的完整工程（包含该工程下所有目录和文件）和此文档一起打包，以组内学生姓名作为文件名，上传提交。例如Stu1_Stu2.zip

代码:

count.h

#pragma once
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#define MAX 0x3f3f3f3f
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
typedef struct  TNode {
    int flag;
    int data;//flag=0 
    char ch;//flag=1
    struct TNode* lChild;//左孩子 
    struct  TNode* rChild;//右孩子 
};
//(5+3*4)*2/3-2*5
 
int cal(struct TNode* root);
int check(char s[], int start, int end);
void postOrder(struct TNode* root);
struct TNode* buildTree(char s[], int start, int end);

main.cpp

#include"count.h"
 
int main(int argc, char** argv) {
    while (1) {
        char a[200];
        printf("请输入表达式:");
        scanf("%s", a);
        printf("你输入的表达式为:%s\n", a);
        struct TNode* b = (struct TNode*)malloc(sizeof(struct TNode));
        b = buildTree(a, 0, strlen(a) - 1);
        printf("Your result is %d\n", cal(b));
    }
    return 0;
}
 
int cal(struct TNode* root) {
    if (root->flag == 1) {
        switch (root->ch) {
        case '+': {
            return cal(root->lChild) + cal(root->rChild);
            break;
        }
        case '-': {
            return cal(root->lChild) - cal(root->rChild);
            break;
        }
        case '/': {
            return cal(root->lChild) / cal(root->rChild);
            break;
        }
        case '*': {
            return cal(root->lChild) * cal(root->rChild);
            break;
        }
        }
    }
    return root->data;
}
int check(char s[], int start, int end) {
    int i;
    int sum = 0;
    int flag = 1;
    if (s[start] == '-') {
        flag = -1;
        start++;
    }
    for (i = start; i <= end; i++) {
        if (!isdigit(s[i])) return MAX;
        sum = sum * 10 + s[i] - '0';
    }
    return sum * flag;
}
void postOrder(struct TNode* root) {
    if (root) {
        postOrder(root->lChild);
        postOrder(root->rChild);
        if (root->flag == 0) {
            printf("%d ", root->data);
        }
        else {
            printf("%c ", root->ch);
        }
    }
}
struct TNode* buildTree(char s[], int start, int end) {
    struct TNode* root = (struct TNode*)malloc(sizeof(struct TNode));
    int cnt = 0;
    int m;
    int i;
    if (start > end) return NULL;
    int posPlusOrSub = 0;//加减号位置 
    int numPlusOrSub = 0;//加减号个数 
    int posDivOrMul = 0;//乘除号位置 
    int numDivOrMul = 0;//乘除号个数 
    int num;
    num = check(s, start, end);
    if (num != 0x3f3f3f3f) {//只有数字 
        root->flag = 0;
        root->data = num;
        root->lChild = NULL;
        root->rChild = NULL;
        return root;
    }
    //有操作符 
    int in_brackets = 0;//不在括号里的标识符 
    for (int k = start; k <= end; k++) {
        if (s[k] == '(') {
            in_brackets++;
        }
        else if (s[k] == ')') {
            in_brackets--;
        }
        if (!in_brackets) {//括号之外 
            if (s[k] == '+' || s[k] == '-') {
                posPlusOrSub = k;
                numPlusOrSub++;
            }
            else if (s[k] == '*' || s[k] == '/') {
                posDivOrMul = k;//乘除号位置 
                numDivOrMul++;//乘除号个数 
            }
        }
    }
    int pos_root;
    //寻找根节点 有加减用加减没加减用乘除 
    if (numPlusOrSub) {
        pos_root = posPlusOrSub;
    }
    else if (numDivOrMul) {
        pos_root = posDivOrMul;
    }
    else {//找不到根 递归再找一次 
        return buildTree(s, start + 1, end - 1);
    }
    root->flag = 1;
    root->ch = s[pos_root];
    root->lChild = buildTree(s, start, pos_root - 1);
    root->rChild = buildTree(s, pos_root + 1, end);
    return root;
}