Unity中的数学基础——变换_unity地层用了仿射变换吗

一：齐次坐标

——齐次坐标就是将原本n维的向量用n+1维来表示，是用于投影几何里的坐标系统。可以这样理解，在Unity中有透视与正交两种相机模式，笛卡尔坐标系是用于正交模式空间下，而齐次坐标系是用于投影模式空间下
——齐次坐标的表示是计算机图形学中的重要手段之一，在笛卡尔坐标下无法区分是一个点还是一个向量，而在齐次坐标下可以明确区分点和向量
——当n+1维的值为0时，表示一个无穷远的点(例如一条平行的火车道，一直向远处看则会相交)，齐次坐标在编写Shader时可能需要用到它

---

二：齐次坐标表示的由来

结论：点的齐次坐标可以表示为(x,y,z,1)，向量的齐次坐标可以表示为(x,y,z,0)，3D坐标系的齐次坐标可以表示为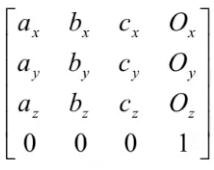

利用向量与点的齐次坐标表示方法可以验证：
——点与点相减后得到的是一个向量
——向量与向量相加减后得到的还是一个向量
——点与向量相加减后得到的是一个点(移动了向量个距离后的点)

---

三：仿射变换

仿射变换=线性变换+平移
因为线性变换需要满足以下三个条件：
——变换前是直线的，变换后依然是直线
——直线比例保持不变
——变换前是原点的，变换后依然是原点
缩放，旋转操作都满足上面三个条件，但是平移操作不满足变换前是原点的，变换后依然是原点这个条件，所以不属于仿射变换。最后得出结论：仿射变换的条件有两个，一是变换前是直线的，变换后依然是直线，二是直线比例保持不变

---

四：变换矩阵模板

因为平移操作不满足线性变换的条件，所以每个矩阵添加了一列去表示平移(tx/ty/tz分别代表在x/y/z轴上的平移的距离)，前面的列表示缩放和旋转，因为3D游戏中一般才会进行矩阵计算，所以Unity中的矩阵都是4*4的

---

五：平移变换

tx代表在x轴上的移动距离，ty代表在y轴上的移动距离，tz代表在z轴上的移动距离

计算一个点p(x,y)或p(x,y,z)经过平移后的点。其实就是一个点移动一个向量的距离，可以理解为一个点与一个向量的加法

---

五：缩放变换

sx代表在x轴上的缩放比例，sy代表在y轴上的缩放比例，sz代表在z轴上的缩放比例

计算一个点p(x,y)或p(x,y,z)经过缩放后的点。可以理解为一个点与不同轴上的缩放系数的乘法

---

六：旋转变换

θ代表旋转的角度 

---

七：变换矩阵的逆矩阵

——平移矩阵的逆矩阵

——缩放矩阵的逆矩阵

——旋转矩阵的逆矩阵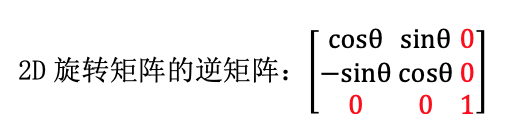

---

八：复合变换

可以把平移，缩放，旋转结合起来形成一个复杂的变换过程，但是矩阵的乘法不满足交换律，所以必须按照顺序相乘。例如一个点先平移再旋转，计算时必须用这个点先乘以平移矩阵再乘以旋转矩阵而不能先乘以旋转矩阵再乘以平移矩阵

---

九：Unity中的变换

——使用Matrix4x4.Translate(matrix)创建一个平移矩阵
——使用Matrix4x4.Rotate(matrix)创建一个旋转矩阵
——使用Matrix4x4.Scale(matrix)创建一个缩放矩阵
——使用Matrix4x4.TRS(matrix)创建一个移动，旋转，缩放的复合矩阵
——使用matrix.MultiplyPoint(point)或matrix.MultiplyPoint3x4(point)实现一个点的复合变换
——使用matrix.MultiplyVector(vector)实现一个向量的复合变换

private void Awake()
{
    //将一个点(1,1,1)平移(2,3,0)的操作
    Vector3 p = new Vector3(1, 1, 1);
    Matrix4x4 matrix = Matrix4x4.Translate(new Vector3(2, 3, 0));
 
    Debug.Log(matrix.MultiplyPoint(p)); //(3,4,1)
}

---

十：通过矩阵变换改变Unity自带Cube的Mesh形状

using UnityEngine;
 
public class Test : MonoBehaviour
{
    private MeshFilter mf;//MeshFilter组件
 
    private Vector3[] oriVertex;//原始顶点数组
    private Vector3[] newVertex;//变换后顶点数组
 
    //变换的参数
    public Vector3 translate;
    public Vector3 rotate;
    public Vector3 scale;
 
    private void Awake()
    {
        mf = GetComponent<MeshFilter>();
 
        oriVertex = mf.mesh.vertices;
        newVertex = new Vector3[oriVertex.Length];
    }
 
    private void Update()
    {
        Quaternion q = Quaternion.Euler(rotate.x, rotate.y, rotate.z);
        Matrix4x4 matrix = Matrix4x4.TRS(translate, q, scale);
        for (int i = 0; i < oriVertex.Length; i++)
        {
            newVertex[i] = matrix.MultiplyPoint3x4(oriVertex[i]);
        }
        mf.mesh.vertices = newVertex;
    }
}