LeetCode 2120.执行所有后缀指令

现有一个 n x n 大小的网格，左上角单元格坐标 (0, 0) ，右下角单元格坐标 (n - 1, n - 1) 。给你整数 n 和一个整数数组 startPos ，其中 startPos = [startrow, startcol] 表示机器人最开始在坐标为 (startrow, startcol) 的单元格上。

另给你一个长度为 m 、下标从 0 开始的字符串 s ，其中 s[i] 是对机器人的第 i 条指令：‘L’（向左移动），‘R’（向右移动），‘U’（向上移动）和 ‘D’（向下移动）。

机器人可以从 s 中的任一第 i 条指令开始执行。它将会逐条执行指令直到 s 的末尾，但在满足下述条件之一时，机器人将会停止：

下一条指令将会导致机器人移动到网格外。
没有指令可以执行。
返回一个长度为 m 的数组 answer ，其中 answer[i] 是机器人从第 i 条指令 开始 ，可以执行的 指令数目 。

示例 1：

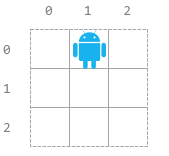
输入：n = 3, startPos = [0,1], s = “RRDDLU”
输出：[1,5,4,3,1,0]
解释：机器人从 startPos 出发，并从第 i 条指令开始执行：

• 0: “RRDDLU” 在移动到网格外之前，只能执行一条 “R” 指令。
• 1: “RDDLU” 可以执行全部五条指令，机器人仍在网格内，最终到达 (0, 0) 。
• 2: “DDLU” 可以执行全部四条指令，机器人仍在网格内，最终到达 (0, 0) 。
• 3: “DLU” 可以执行全部三条指令，机器人仍在网格内，最终到达 (0, 0) 。
• 4: “LU” 在移动到网格外之前，只能执行一条 “L” 指令。
• 5: “U” 如果向上移动，将会移动到网格外。
  示例 2：

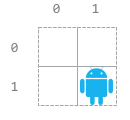
输入：n = 2, startPos = [1,1], s = “LURD”
输出：[4,1,0,0]
解释：

• 0: “LURD”
• 1: “URD”
• 2: “RD”
• 3: “D”
  示例 3：

输入：n = 1, startPos = [0,0], s = “LRUD”
输出：[0,0,0,0]
解释：无论机器人从哪条指令开始执行，都会移动到网格外。

提示：

m == s.length
1 <= n, m <= 500
startPos.length == 2
0 <= startrow, startcol < n
s 由 ‘L’、‘R’、‘U’ 和 ‘D’ 组成

法一：直接模拟：

class Solution {
public:
    vector<int> executeInstructions(int n, vector<int>& startPos, string s) {
        vector<int> ans;
        for (int i = 0; i < s.size(); ++i)
        {
            vector<int> curPos = startPos;
            int curAns = 0;
            for (int j = i; j < s.size(); ++j)
            {
                if (s[j] == 'L')
                {
                    --curPos[1];
                }
                else if (s[j] == 'R')
                {
                    ++curPos[1];
                }
                else if (s[j] == 'U')
                {
                    --curPos[0];
                }
                else if (s[j] == 'D')
                {
                    ++curPos[0];
                }

                if (curPos[0] < 0 || curPos[0] > n - 1 || curPos[1] < 0 || curPos[1] > n - 1)
                {
                    break;
                }
                ++curAns;
            }
            ans.push_back(curAns);
        }

        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

如果s的长度为m，则此算法时间复杂度为O(m${}^2$)，空间复杂度为O(1)。

法二：我们先无视网格边界，计算出执行完所有指令后的坐标，然后从后往前遍历指令，每遍历到一个指令，我们先保存下来这个指令后面还有几个指令（即倒序遍历到了当前第几个），然后undo这条指令，然后再计算当前位置与起始位置的偏移，这个偏移可以看做网格的偏移而非机器人的偏移，计算出网格的偏移后，我们可以计算出新的出界条件，开始时是x或y为-1到n时出界，现在出界条件要加上偏移量。然后，核心思想是，我们是知道当前位置距离结束还有几个指令的，我们也知道边界条件下到指令结束还有几个指令（前面每遍历到一个位置保存的），因此两者相减就是还可执行的指令数：

class Solution {
public:
    vector<int> executeInstructions(int n, vector<int>& startPos, string s) {
        int x = startPos[1];
        int y = startPos[0];
        for (char c : s)
        {
            if (c == 'U')
            {
                --y;
            }
            else if (c == 'D')
            {
                ++y;
            }
            else if (c == 'L')
            {
                --x;
            }
            else if (c == 'R')
            {
                ++x;
            }
        }

        vector<int> ans(s.size());
        map<int, int> dx;
        map<int, int> dy;
        for (int i = s.size() - 1; i >= 0; --i)
        {
            // 记录到当前位置到命令串终止还有几个指令
            dx[x] = s.size() - i;
            dy[y] = s.size() - i;

            // undo指令，为了下步遍历做准备
            if (s[i] == 'U')
            {
                ++y;
            }
            else if (s[i] == 'D')
            {
                --y;
            }
            else if (s[i] == 'L')
            {
                ++x;
            }
            else if (s[i] == 'R')
            {
                --x;
            }

            // 获取当前位置到起始位置的偏移
            // 我们接下来要把整个网格移动这个偏移量
            // 我们要先undo指令再计算偏移量，因为这才是执行当前遍历到的指令前的位置
            // 举例来说，第一次遍历时玩家位置在执行完最后一条指令后的位置
            int xDiff = x - startPos[1];
            int yDiff = y - startPos[0];

            // 原本是到-1或n时出界，由于网格也偏移了，加上偏移量，得到新的出界条件
            // 这一步是获取在网格偏移后的界限上，到终止还有几个指令
            // 之所以要取max，举例来解释，如果2×2的格子先向上移动100次，再向下移动200次
            // 那么我们应该取首次出界时后面还有几个指令
            int afterEndInstructionNum = max({dx[-1 + xDiff], dx[n + xDiff], dy[-1 + yDiff], dy[n + yDiff]});

            ans[i] = s.size() - i - afterEndInstructionNum;
        }

        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

如果s的长度为m，则此算法时间复杂度为O(m)，空间复杂度为O(m)。