- 1279.【华为OD机试真题】运输时间(贪心算法—Java&Python&C++&JS实现)_华为od机考算法题:运输时间
- 2【NLP】图神经网络解释以及如何使用 PyTorch 使用_gnn mlp llm
- 3标点符号表情_`′
- 4react echarts制作曲线图(以天气预报为例)_react实现曲线图
- 5修改android 系统设置 android 版本_ro.product.model
- 6SpringBoot+Maven多环境配置模式
- 7关于java常见异常举例_java非法参数异常
- 8阿里云企业级 Kubernetes 部署方案详解
- 9Python--执行外部命令subprocess_python subprocess.run 不输出到终端
- 10一文让你更了解linux设备树_properties must precede subnodes
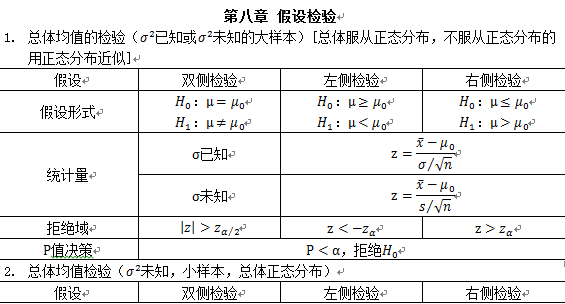
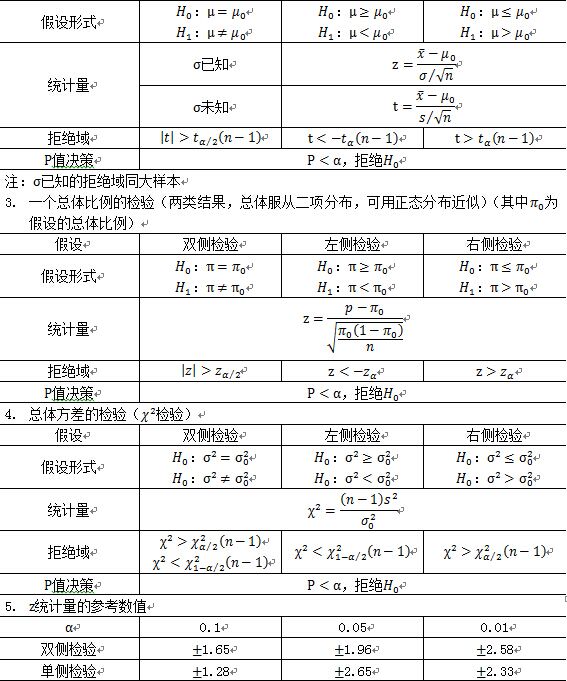
几种常见的假设检验_假设检验四种情况
赞
踩
定义
假设的形式
H0——原假设,
双侧检验:H0:μ = μ0 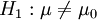
单侧检验: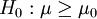
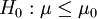 ,
,
目的:比较样本均数 所代表的未知总体均数μ和已知总体均数μ0。
计算公式:
t统计量: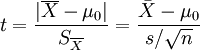
自由度:v=n - 1
适用条件:
(1) 已知一个总体均数;
(2) 可得到一个样本均数及该样本标准误;
(3) 样本来自正态或近似正态总体。
T检验的步骤
1、建立虚无假设H0:μ1
2、计算统计量T值,对于不同类型的问题选用不同的统计量计算方法;
1)如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度,其统计量T值的计算公式为:
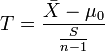
2)如果要评断两组样本平均数之间的差异程度,其统计量T值的计算公式为:
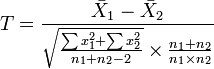
3、根据自由度df=n-1,查T值表,找出规定的T理论值并进行比较。理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值记为T(df)0.01和T(df)0.05
4、比较计算得到的t值和理论T值,推断发生的概率,依据下表给出的T值与差异显著性关系表作出判断。
| T值与差异显著性关系表 | ||
|---|---|---|
| T | P值 | 差异显著程度 |
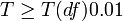 | 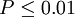 | 差异非常显著 |
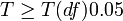 | 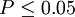 | 差异显著 |
| T | P | 差异不显著 |
5、根据是以上分析,结合具体情况,作出结论。
T检验的应用领域:
T检验可用于比较药物治疗组与安慰剂治疗组病人的测量差别。
第一步:建立虚无假设
第二步:计算统计量Z值,对于不同类型的问题选用不同的统计量计算方法,
1、如果检验一个样本平均数( )与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为:
)与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为:
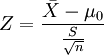
其中:
2、如果检验来自两个的两组样本平均数的差异性,从而判断它们各自代表的总体的差异是否显著。其Z值计算公式为:
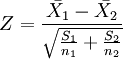
其中:
-
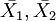 是样本1,样本2的平均数;
是样本1,样本2的平均数; - S1,S2是样本1,样本2的标准差;
- n1,n2是样本1,样本2的容量。
第三步:比较计算所得Z值与理论Z值,推断发生的概率,依据Z值与差异显著性关系表作出判断。如下表所示:
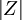 | P值 | 差异程度 |
|---|---|---|
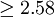 | 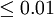 | 非常显著 |
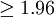 | 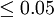 | 显著 |
| <1.96 | >0.05 | 不显著 |
第四步:根据是以上分析,结合具体情况,作出结论。