【Runge-Kutta】龙格-库塔法求解微分方程matlab仿真_龙格库塔法matlab

1.软件版本

MATLAB2013b

2.算法理论

       龙格－库塔法（Runge-Kutta）是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。龙格库塔法的家族中的一个成员如此常用，以至于经常被称为“RK4”或者就是“龙格库塔法”。令初值问题表述如下。

       这样，下一个值(yn+1)由现在的值(yn)加上时间间隔(h)和一个估算的斜率的乘积决定。该斜率是以下斜率的加权平均：

        k1是时间段开始时的斜率；

        k2是时间段中点的斜率，通过欧拉法采用斜率k1来决定y在点tn + h/2的值；

        k3也是中点的斜率，但是这次采用斜率k2决定y值；

        k4是时间段终点的斜率，其y值用k3决定。

3.部分matlab程序 

clc;
clear;
close all;
warning off;
 
%The parameter
 
 
g  = 9.81;
L  = 0.1;
m  = 0.5;
es = 2;
%the range of t
t0    = 0;
tf    = 10;
x0    = 0.25;
x0dot = 0;
Step  = 1000;
%The method of RK4 
Y1    = func_4RGKT(t0,tf,x0,x0dot,Step);
 
figure(1);
subplot(121);
plot([t0:(tf-t0)/Step:tf],Y1,'b');
xlabel('t');
ylabel('x');
axis square;
grid on;
title('the method of RK4');
 
 
%The method of Euler                         
Y2    = func_Euler(t0,tf,x0,x0dot,Step);	
figure(1);
subplot(122);
plot([t0:(tf-t0)/Step:tf],Y2,'r');
xlabel('t');
ylabel('x');
axis square;
grid on;
title('the method of Euler');
 
 
 

function Y1 = func_4RGKT(t0,tf,x0,x0dot,STEPS);                    
 
%t0, tf, upper and lower, respectively,
%x0  the initial value of y,
%STEPS steps times
 
h        = (tf - t0)/STEPS;                     
T        = zeros(1,STEPS+1);                                  
Y        = zeros(1,STEPS+1);
T(1)     = t0;                                          
Y(1)     = x0;
Y0dot(1) = x0dot;
 
for j=1:STEPS                                     
    tj         = T(j);
    yj         = Y(j);
    yjd        = Y0dot(j);
    
    k1         = h*func_function(tj     ,[yj,yjd]);
    
    k2         = h*func_function(tj+h/2 ,[yj+h*k1(1)/2,yjd+h*k1(2)/2]); 
    
    k3         = h*func_function(tj+h/2 ,[yj+h*k2(1)/2,yjd+h*k2(2)/2]);     
    
    k4         = h*func_function(tj+h   ,[yj+h*k3(1)  ,yjd+h*k3(2)]);         
 
    Y(j+1)     = yj  + (k1(1) + 2*k2(1) + 2*k3(1) + k4(1))/6;
    Y0dot(j+1) = yjd + (k1(2) + 2*k2(2) + 2*k3(2) + k4(2))/6;
    T(j+1)     = t0 + h*j;
end
 
Y1=Y';                 
 
 

4.仿真结论

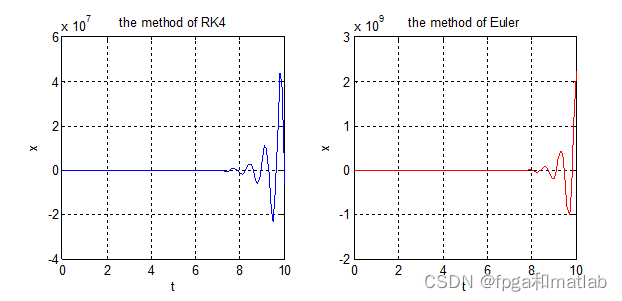
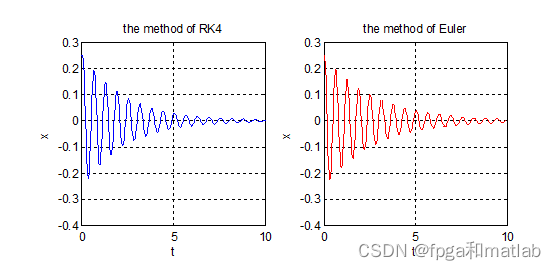
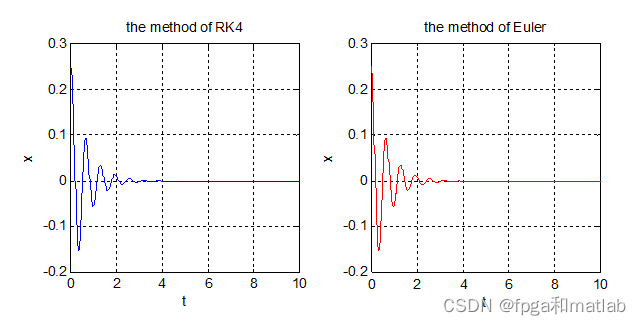
         从图的仿真结果可知，当算法迭代1000次的时候，算法经过几个周期抖动之后收敛，但是其收敛时间较短。 因此，从整体而言，采用RK4算法，比Euler算法收敛更快，且较快的达到一定精度之内A28-20。