假设检验_到底该怎么理解假设检验？

学过统计学或概率论的同学，对“假设检验”这个词一定不陌生。因为期末考试的卷子里必定会考一道这种题，那个时候，我其实对假设检验的流程并不是很理解，不过幸好流程简单，照葫芦画瓢，套一套格式就能答对。那假设检验到底是个什么东西？

先上一道假设检验的例题，回忆一下假设检验的流程，找一下当初的感觉。

某机床厂加工一种零件，根据经验知道，该厂加工零件的椭圆度渐近服从正太分布，其总体均值为0.081mm，今另换一种新机床进行加工，取200个零件进行检验，得到椭圆度均值为0076mm，样本标准差为0.025mm,问新机床加工零件的椭圆度总体均值与以前有无显著差别？
解：该题问新旧机床加工零件的椭圆度有无显著差别，很明显是一个双侧检验问题。
假设：

：μ = 0.081mm 没有显著差别

：μ != 0.081mm 有显著差别

且由题可知 n>30，为大样本量，故采取z统计量。
z =

=

= -2.83

取显著性水平

= 0.05 （即原假设正确时却被拒绝的概率或风险）

查表得到临界值：

=

1.96

故

>

,根据决策准则，拒绝

,可以认为新老机床加工零件椭圆度得均值有显著差别。

（

代表x的平均值）

看完了一遍解题思路。

我说一下我当时学这门课时做这种题的感受：

看题的时候觉得条件给的都很简单嘛，不难不难，小意思

看完题之后，我艹，他在说啥啊！！！！

于是开始看答案，看到假设

看到用z统计量， z =

的时候，我艹 ？，咋回事啊，又看不懂了。

于是，每次做这种题的时候都要翻开课本，对着例题套格式。

现在我们来抽丝剥茧一下为什么过程要这样写？

先说一下，我个人对假设检验的核心思想的看法：就是给出一个标准，把该标准代入所要考察的情况中，看是否会发生小概率事件，如果发生，则所要考察的情况不符合该标准，如果没发生小概率事件，则符合标准。

举一个类似的例子：我们在做数学选择题的时候，当我们从题中所给的条件算不出答案的时候，我们会采用代入法，把ABCD四个选项代入题目中，看哪个符合条件！

而假设检验也正是这种思路

以上题为例，首先给大家捋清楚几个点：

1、0.081mm是我们期待的一个标准，与当前的零件没有实质性的关系。

2、样本均值

3、样本均值的数学期望为总体均值即E(

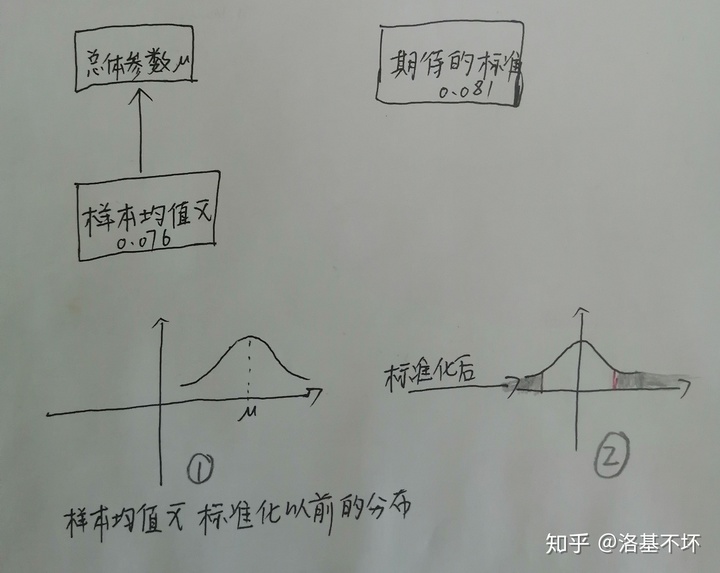
首先假设

然后是z统计量部分： z =

我们知道这个式子是对

（统计量

而意义也在于将其分布曲线从以

所以我们假设μ = 0.081mm为

这样我们就可以通过查表来获取每个值的概率，即可以通过查表知道当

不知道我有没有说清楚.........害，水平不行。

刚才的是双侧检验，然后说一下左单侧检验和右单侧检验

这两种问题的关键是：原假设和备择假设怎么设的问题？常见的设法为

或

很多同学可能都听过老师说：一定要把等号放在原假设里边。

为什么呢？等号肯定要放在原假设了因为我们要用μ = 1000或μ = 1200代入到z或t统计量当中，进行标准化。你把等号放到备择假设我们就不能用了。

还有一点就是我们到底是在原假设中写大于号还是小于号？

这个要看是左单侧检验还是右单侧检验，

左单侧检验的话，拒绝域就在左侧，即临界值为负值，看公式 z =

如果μ = 1000，你都为小于临界值，进入了拒绝域，那μ>1000，岂不是更小于临界值

同理，右单侧检验，拒绝域在右侧，临界值为正值，还是看公式 z =

如果μ = 1200，你都大于临界值，进入了拒绝域，那μ<1200，岂不是更大于临界值

所以回过头来看假设检验其实就分为两步：

1：假设：假设它符合或不符合某个标准，进而继续往下推理

2：检验：检验我们在假设的基础得到的结论是否符合逻辑