木道寻08

这个屌丝很懒，什么也没留下！

热门标签

【数据结构】二叉树(C语言)

作者：木道寻08 | 2024-06-28 20:40:43

踩

【数据结构】二叉树(C语言)

前言：

在前面介绍到的栈、队列等利用数组或是链表实现的数据结构，其实属于一种一对一的线性结构，接下来我们要介绍的是一种关系为一对多的非线性结构，在实际场景中也会多次见到，例如学校的成员职位结构表，公司职员结构等，都会经常见到类似结构，不仅如此，考研及其他考试中也会涉及到对二叉树的知识的考察，因此这部分内容十分重要，下面将开启知识之旅

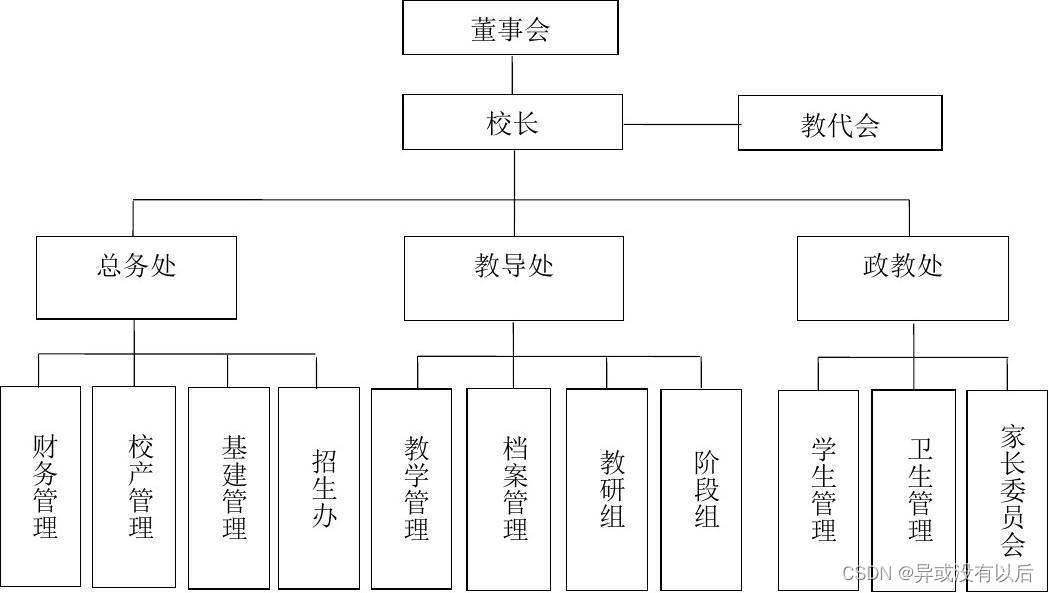
一、树的介绍

1.1树的概念

树是一种 非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的 。

有一个 特殊的结点，称为根结点 ，根节点没有前驱结点

除根节点外，其余结点被分成 M(M>0) 个互不相交的集合 T1 、 T2 、 …… 、 Tm ，其中每一个集合 Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有 0 个或多个后继

因此，树是递归定义 的。

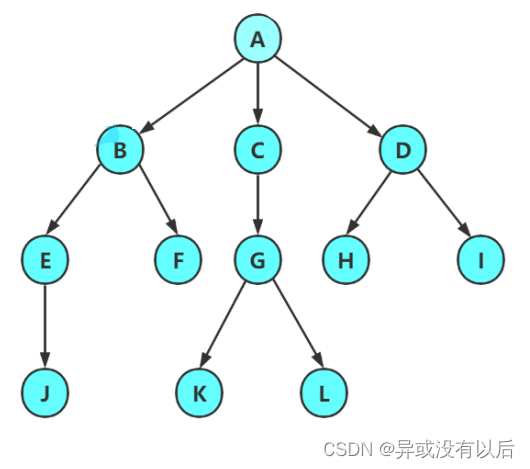
注意：树形结构中，子树之间不能有交际否则就不是树形结构

1.2树的相关术语

节点的度 ：一个节点含有的子树的个数称为该节点的度；如上图： A 的为3

叶节点或终端节点 ：度为 0 的节点称为叶节点；如上图：J 、F 、k 、L ... 等节点为叶节点

非终端节点或分支节点 ：度不为 0 的节点；如上图： D 、 E 、 G... 等节点为分支节点

双亲节点或父节点 ：若一个节点含有子节点，则这个节点称为其子节点的父节点；如上图： A 是 B 的父节点

孩子节点或子节点 ：一个节点含有的子树的根节点称为该节点的子节点；如上图： B 是 A 的孩子节点

兄弟节点 ：具有相同父节点的节点互称为兄弟节点；如上图： B 、 C 是兄弟节点

树的度 ：一棵树中，最大的节点的度称为树的度；如上图：树的度为3

节点的层次 ：从根开始定义起，根为第 1 层，根的子节点为第 2 层，以此类推；

树的高度或深度 ：树中节点的最大层次；如上图：树的高度为 4

堂兄弟节点 ：双亲在同一层的节点互为堂兄弟；如上图： H 、 I 互为兄弟节点

节点的祖先 ：从根到该节点所经分支上的所有节点；如上图： A 是所有节点的祖先

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是 A 的子孙

森林：由 m （ m>0 ）棵互不相交的树的集合称为森林；

1.3树的表示

树相对线性表就比较复杂了，要存储表示起来就比较麻烦，既要保存值域，又要保存节点与节点之间的关系，实际中树的表示方法有很多：双亲表示法，孩子表示法，孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

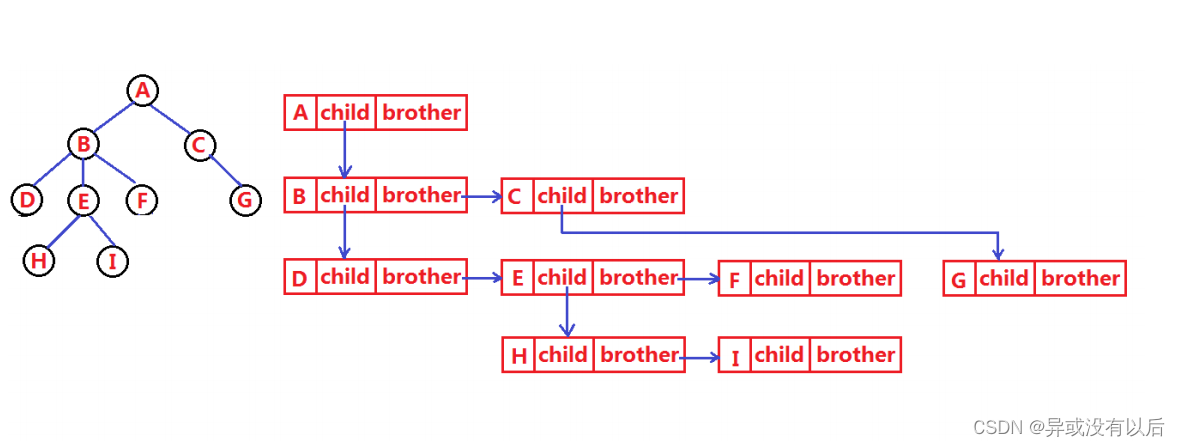
孩子兄弟表示法，其逻辑就是把原来树中的兄弟，变成了二叉树中的父子，其转化就是树转化成二叉树的相关知识，会在后面介绍，这里不详讲。

1.4树在实际场景中的应用

二、二叉树概念及结构

2.1 概念

二叉树是一种常见的树状数据结构，它由若干个节点组成，这些节点通过边连接起来。每个节点最多可以有两个子节点，分别称为左子节点和右子节点。

二叉树的特点是每个节点最多有两个子节点，而且左子节点和右子节点的位置是固定的。通常，左子节点小于或等于父节点，右子节点大于父节点，这种顺序被称为搜索二叉树。

二叉树的一个重要概念是根节点，它是树的起始节点，其他节点通过边与根节点相连。根节点没有父节点。另外，每个节点除了子节点的连接外，还可以有一个指向父节点的连接，这样就形成了一个双向连接的二叉树。

一棵二叉树是节点的的有限结合，该集合：

或者为空
由一个根节点加上两棵别称为左子树和右子树的二叉树组成

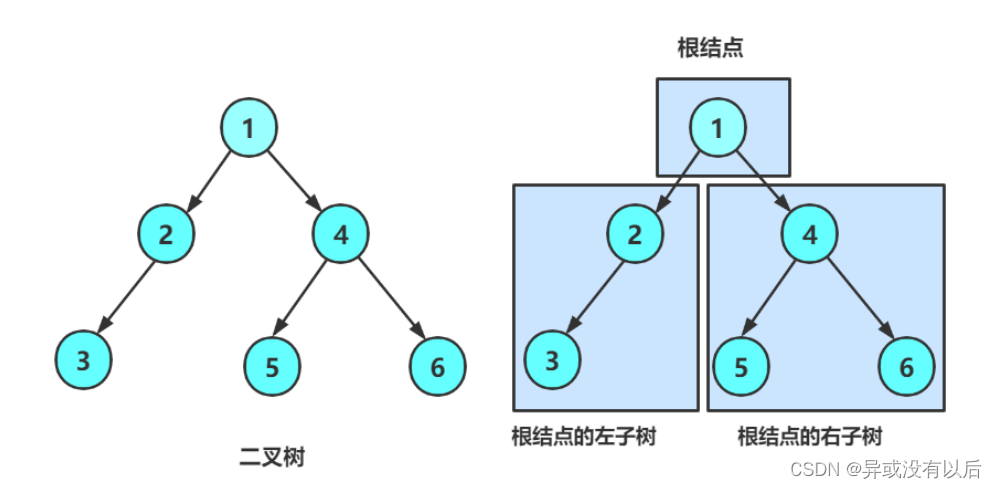
由上图可以得知：

二叉树不存在度大于2的节点
二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

注意：任意的二叉树都是由以下几种情况复合而成的：

2.2 现实中的二叉树

2.3特殊的二叉树

1. 满二叉树 ：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K ，且结点总数是，则它就是满二叉树。

2. 完全二叉树 ：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为 K的，有n 个结点的二叉树，当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

2.4二叉树的性质

1. 若规定根节点的层数为 1 ，则一棵非空二叉树的 第 i 层上最多有2^(i-1)个结点.

2. 若规定根节点的层数为 1 ，则 深度为 h 的二叉树的最大结点数是2^h-1

3. 对任何一棵二叉树 , 如果度为 0, 其叶子结点个数为n0 , 度为 2 的分支结点个数为n2 , 则有 n0＝ n2＋ 1

4. 若规定根节点的层数为 1 ，具有 n 个结点的满二叉树的深度 ， h= log(n+1)(ps：是log 以 2为底，n+1 为对数 )

5. 对于具有 n 个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从 0 开始编号，则对于序号为i 的结点有：

1. 若 i>0 ， i 位置节点的双亲序号： (i-1)/2 ； i=0 ， i 为根节点编号，无双亲节点

2. 若 2i+1<n ，左孩子序号： 2i+1 ， 2i+1>=n 否则无左孩子

3. 若 2i+2<n ，右孩子序号： 2i+2 ， 2i+2>=n 否则无右孩子

ps:在考试中经常会涉及到树及叶子节点的层数关系之间的计算，需多加注意

三、二叉树的存储结构及实现

二叉树可以使用两种存储结构，一种是顺序存储，另一种是链式存储

3.1二叉树的顺序存储

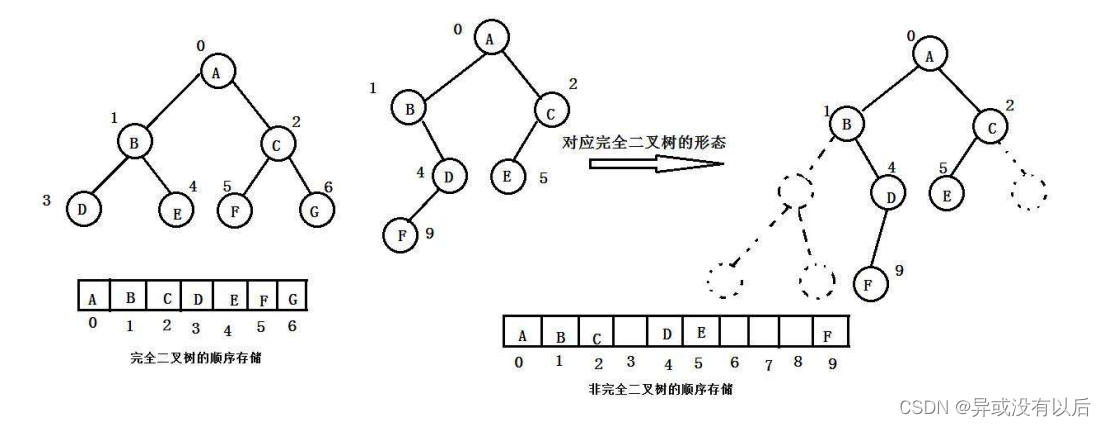
顺序结构存储就是使用 数组来存储 ，一般使用数组 只适合表示 完全二叉树 ，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我前面的文章已经专门讲解过。二叉树顺 序存储在物理上是一个数组，在逻辑上是一棵二叉树。详见上篇文章

3.2二叉树的链式存储

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链，当前我们学习中一般都是二叉链，后面章节学到高阶数据结构如红黑树等会用到三叉链。

3.2.1 前置说明

在学习二叉树的基本操作之前，我们学要先学会构建一个二叉树，而后学习二叉树的相关操作。如何快速手搓一个二叉树？代码如下：


typedef int BTDataType;
typedef struct BTNode
{
    struct BTNode* leftchild;
    struct BTNode* rightchild;
    BTDataType val;
}BTNode;
 
//为结点开辟空间
BTNode* BuyNode(int val)
{
    BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
    if (newnode == NULL)
    {
        perror("malloc fail");
        return;
    }
    newnode->val = val;
    newnode->leftchild = NULL;
    newnode->rightchild = NULL;
    return newnode;
 
}
 
//创造二叉树结构
BTNode* CreateTree()
{
    BTNode* n1 = BuyNode(1);
    BTNode* n2 = BuyNode(2);
    BTNode* n3 = BuyNode(3);
    BTNode* n4 = BuyNode(4);
    BTNode* n5 = BuyNode(5);
    BTNode* n6 = BuyNode(6);
 
    n1->leftchild = n2;
    n1->rightchild = n4;
    n2->leftchild = n3;
    n4->leftchild = n5;
    n4->rightchild = n6;
 
    return n1;
}
 
//主函数调用以上函数
int main()
{
    BTNode* root = CreateTree();
 
	return 0;
}

其逻辑结构如图所示：

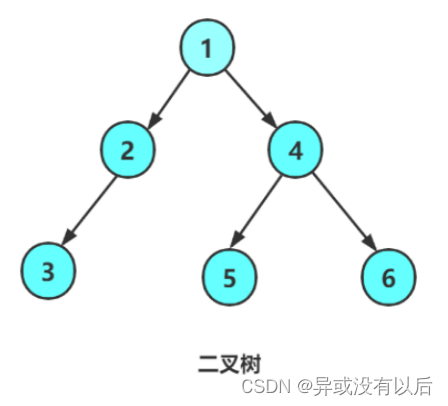
注意：上述代码并非创建二叉树的方式，真正创建二叉树的方式会在后面重点讲解。

在看二叉树的基本操作之前，我们再回顾一遍二叉树概念：

1. 空树

2. 非空：根节点，根节点的左子树、右子树组成的

从概念中可以看出，二叉树定义是递归式的，因此后续基本操作中基本都是按照该概念实现的。

四、二叉树的主要功能

4.1二叉树的遍历

4.1.1 前序、中序、以及后序遍历

学习二叉树，最简单的操作的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所作的操作依赖于具体的应用问题。遍历二叉树是二叉树上最重要的运算之一，也是二叉树上进行其他运算的基础。

按照规则，二叉树的遍历有：前序 / 中序 / 后序的递归结构遍历 ：

1. 前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。

2. 中序遍历 (Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中（间）。

3. 后序遍历 (Postorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根，所以 N(Node ）、 L(Left subtree ）和 R(Right subtree ）又可解释为： 根、根的左子树和根的右子树 。 NLR 、 LNR 和 LRN 分别又称为先根遍历、中根遍历和后根遍历。

(1) 前序：


// 二叉树前序遍历
 
void PreOrder(BTNode* root)
{
    //若为空，则打印N，用于熟悉树的根节点结构
    if (root == NULL)
    {
        print("N ");
        return;
    }
    //若不为空，则打印根的值
    printf("%d ", root->val);
    // 递归，遍历树的左子树
    PreOrder(root->leftchild);
    // 递归，遍历树的右子树
    PreOrder(root->rightchild);
}

(2) 中序:


// 二叉树中序遍历
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
 
    // 遍历树的左子树
    InOrder(root->leftchild);
 
    // 遍历完之后才打印根节点的值
    printf("%d ", root->val);
 
    // 遍历树的右子树
    InOrder(root->rightchild);
}

(3) 后序:


// 二叉树后序遍历
 
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
    // 遍历左子树
    InOrder(root->leftchild);
    // 遍历右子树
    InOrder(root->rightchild);
    //左右子树都遍历完，再打印根节点的值
    printf("%d ", root->val);
}

4.2 计算树的节点个数


// 计算树中总结点个数
int TreeSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
// 利用递归实现
    return TreeSize(root->leftchild) + TreeSize(root->rightchild) + 1;
 
}

先遍历一遍左子树，累加，再遍历右子树，累加。最后，加上根节点(+1)。

其内在递归过程如图：

4.3 计算树的高度


// 计算树的高度
int TreeHeight(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
 
    int lefttree = TreeHeight(root->leftchild);
    int righttree = TreeHeight(root->rightchild);
    // 利用递归累加得层数
    return lefttree > righttree ? lefttree+1 : righttree+1 ;
}

注意：这里易犯的一个错误是，不使用变量lefttree和righttree，而是直接return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1; 这种不止一次调用递归的方法，导致的结果就是时间复杂度达到O(2^n), 极易导致系统崩溃

递归过程如图所示(图像由于太大，可能未能保持原貌，但希望能了解其思路即可)：

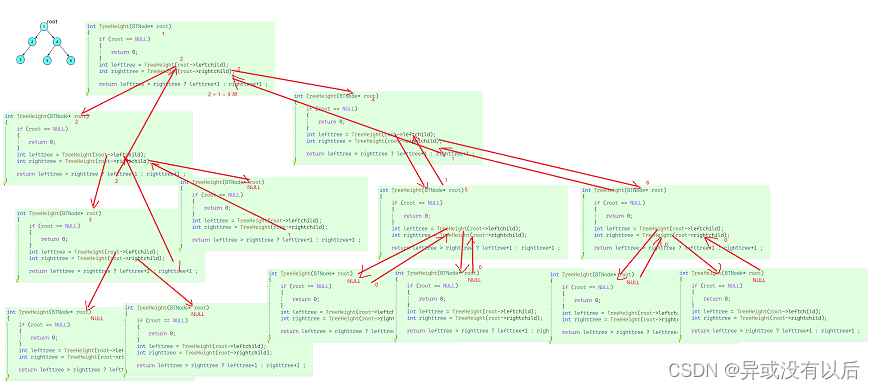
4.4 计算第k层结点的个数


// 返回第k层的结点数
int TreeLevel(BTNode* root, int k)
{
    if (root == NULL)
    {
        return 0;
    }
 
    if (k == 1)
        return 1;
     
    // 从第一层出发(根节点所在的层)，层层递归，使k-1，当k等于1时，即为第k层
    return TreeLevel(root->leftchild, k - 1) + TreeLevel(root->rightchild, k - 1);
}

此处不再粘贴其递归过程，如有关于递归过程不甚了解的小伙伴可以私聊我捏~免费解答

4.5 查找树中 x 的值


// 查找与x相等的结点
BTNode* FindTree(BTNode* root, int x)
{
    if (root == NULL)
        return NULL;
 
    if (root->val == x)
        return root;
    
    // 注意在递归的过程中，一定要定义一个BTNode*类型的变量来接收递归返回的值，否则后果讲不可预测(结果视编译环境不同而不同)
    BTNode* ret1 = FindTree(root->leftchild, x);
    if (ret1)
        return ret1;
 
    BTNode* ret2 = FindTree(root->rightchild, x);
    if (ret2)
        return ret2;
 
    return NULL;
}

五、源码呈现

test.c


#define _CRT_SECURE_NO_WARNINGS 1
 
#include<stdio.h>
#include<stdlib.h>
 
typedef int BTDataType;
typedef struct BTNode
{
    struct BTNode* leftchild;
    struct BTNode* rightchild;
    BTDataType val;
}BTNode;
 
BTNode* BuyNode(int val)
{
    BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
    if (newnode == NULL)
    {
        perror("malloc fail");
        return NULL;
    }
    newnode->val = val;
    newnode->leftchild = NULL;
    newnode->rightchild = NULL;
    return newnode;
 
}
BTNode* CreateTree()
{
    BTNode* n1 = BuyNode(1);
    BTNode* n2 = BuyNode(2);
    BTNode* n3 = BuyNode(3);
    BTNode* n4 = BuyNode(4);
    BTNode* n5 = BuyNode(5);
    BTNode* n6 = BuyNode(6);
 
    n1->leftchild = n2;
    n1->rightchild = n4;
    n2->leftchild = n3;
    n4->leftchild = n5;
    n4->rightchild = n6;
 
    return n1;
}
 
void PreOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
 
    printf("%d ", root->val);
    PreOrder(root->leftchild);
    PreOrder(root->rightchild);
}
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
 
    InOrder(root->leftchild);
    printf("%d ", root->val);
    InOrder(root->rightchild);
}
void PostOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
 
    InOrder(root->leftchild);
    InOrder(root->rightchild);
    printf("%d ", root->val);
}
 
int TreeSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    return TreeSize(root->leftchild) + TreeSize(root->rightchild) + 1;
 
}
 
int TreeHeight(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    int lefttree = TreeHeight(root->leftchild);
    int righttree = TreeHeight(root->rightchild);
 
    return lefttree > righttree ? lefttree+1 : righttree+1 ;
}
 
int TreeLevel(BTNode* root, int k)
{
    if (root == NULL)
    {
        return 0;
    }
 
    if (k == 1)
        return 1;
 
    return TreeLevel(root->leftchild, k - 1) + TreeLevel(root->rightchild, k - 1);
}
 
BTNode* FindTree(BTNode* root, int x)
{
    if (root == NULL)
        return NULL;
 
    if (root->val == x)
        return root;
 
    BTNode* ret1 = FindTree(root->leftchild, x);
    if (ret1)
        return ret1;
 
    BTNode* ret2 = FindTree(root->rightchild, x);
    if (ret2)
        return ret2;
 
    return NULL;
}
 
int main()
{
    BTNode* root = CreateTree();
 
    PreOrder(root);
    printf("\n");
    int a = TreeSize(root);
    printf("%d\n", a);
 
    int b = TreeHeight(root);
    printf("%d\n", b);
 
    int c = TreeLevel(root, 2);
    printf("%d\n", c);
 
    BTNode* pd = FindTree(root, 3);
    printf("%d\n", pd->val);
    // 查找结点，还可以进行修改
    pd->val++;
    PreOrder(root);
    printf("\n");
	return 0;
}

六、说在最后

6.1题外话

递归及函数栈帧知识点不熟悉的可以翻翻前人的文章，讲得真的很透彻！

http://t.csdnimg.cn/h2ElD

6.2 递归的思想可以概括为两点：

（1）递归子问题(步步拆解)

（2）返回条件(最小子问题)

6.3 每文一句

两点之间的最短距离是恶性循环。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/木道寻08/article/detail/767198