第十三届蓝桥杯A组Python组心得分享

第一次写心得类的文章，趁着假期有时间，记录一下在准备这个比赛间的一些心得和一些问题的思路。（前面是碎碎念，直接看问题解决思路的可以跳到后面）

先说情况：省一，小题对了第一个，大题写出来了五个（不确定是否全部AC），认真准备这个比赛的时间不超过一周，中间还要上课交作业啥的。希望个人的经验能对后来的同学有所帮助（最开始报名这个比赛是想着能够在寒假认真提升一下自己的编程能力的（结果还是划水，在赛前抱的佛脚，感谢我的好舍友在我碰见难题的时候给我帮助！！！！有个大佬舍友人生之幸QWQ

关于蓝桥杯：

我之前也考虑过要不要参加这个比赛，主要想着还是比较贵，但是感谢学校给我报销的机会，当时就想着拿省奖报销混个奖状，但是最后又变成了省一才能报销，所以也有了动力稍微认真准备了一下，比赛题目的确不难，对于巨佬来说不值一提，对我来说算是一个锻炼的过程吧，报名python是因为python编程相对简单；这个比赛带给我了不少东西，在过程中也接触到了力扣之类的刷题网站，也没有之前的那种惧怕的感觉了，还带上了我的舍友一起刷力扣，对我来说也算有收获

关于考场设备：

因为疫情，官方建议线上，我们学校提供了教室，采取自愿的方式，因为统一地方对我来说比较方便，自己带电脑机房不提供电脑，我觉得这样比较方便是因为我可以用自己电脑键盘鼠标啥的都比较熟悉，同时可以不用自己准备考试环境，之前不想一个人比就是因为感觉正面背面啥的录像很麻烦加上找不到空闲教室。如果学校不提供这个环境的听说寝室也可以，设备这些提前弄好，在正式比前一天考场的wifi还特别差，后面找同学才解决这个问题，这些都是一些需要提前准备的东西。

关于python组准备

除了一些刷题网站外，考前能做一两次往年的对应考题我觉得就差不多够了，知道这个比赛会有大题小题，每个题大概多难就差不多了。以往的小题会多一点，听说今年是因为线上大题变多，这样也挺好的，因为小题我也不一定能做对，大题多能拉低大题难度（bushi），事实证明我的运气比较好）

一些小技巧

蓝桥杯听说称为暴力杯，这一点不假，很多问题可以暴力破解。比赛提供草稿，可以使用电脑自带计算器和office，小题不要求只是建议代码解决，那么就拿分直接做出答案也就没有问题。我在准备的时候也遇到了相似的题，这种题目可以直接被excel或者计算器秒解，也不浪费时间，比如本次第一次裁纸题，找到规律可以节约时间留给后续的题目，一些和时间日期有关的、字符编码有关的都可以用到。相关的题目我举两个比较典型，后续有时间也可以补充一下其他小技巧，网上这类型的博文也很多，感兴趣可以了解一些这类小trick：

第几天

【问题描述】

2000年的1月1日，是那一年的第1天。

那么，2000年的5月4日，是那一年的第几天？

【答案】

125

excel文本框调成时间模式，一拖就出来了，之前还搞过手算，但都比不上excel。

年号字符

【问题描述】

小明用字母 A对应数字 1，B对应 2，以此类推，用 Z对应 26。

对于 27以上的数字，小明用两位或更长位的字符串来对应，例如 AA对应27，AB对应28，AZ对应52，LQ对应329。

请问2019对应的字符串是什么？

【答案】（26进制问题）

BYQ（2*26^2+25*26^1+17=2019）

 

 、

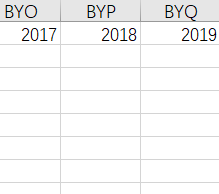
本次考题思路分享

（可能存在很多问题，因为比赛以后我就把我没做出来的题看了一下题解，做出的题和同学探讨了一下思路，肯定有很多可以优化的地方，欢迎大家指正）

试题 A: 裁纸刀 本题总分：5 分 【问题描述】 小蓝有一个裁纸刀，每次可以将一张纸沿一条直线裁成两半。 小蓝用一张纸打印出两行三列共 6 个二维码，至少使用九次裁出来，下图 给出了一种裁法。在上面的例子中，小蓝的打印机没办法打印到边缘，所以边缘至少要裁 4 次。另外，小蓝每次只能裁一张纸，不能重叠或者拼起来裁。 如果小蓝要用一张纸打印出 20 行 22 列共 440 个二维码，他至少需要裁多 少次？

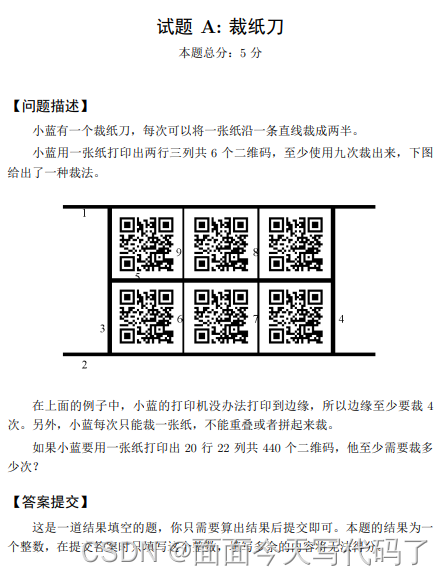
第一题：443，当时应该就是直接通过一些计算得到的，签到题。长a宽b，周围需要切4刀，中间需要切a-1刀，剩下需要a*(b-1)刀，那么一共需要a*b+3刀

试题 B: 寻找整数 本题总分：5 分 【问题描述】 有一个不超过 1017 的正整数 n，知道这个数除以 2 至 49 后的余数如下表 所示，求这个正整数最小是多少。

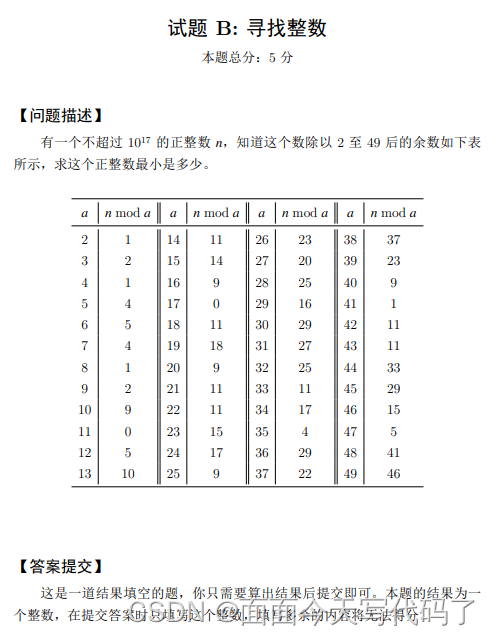
 答案：2022040920220409，这个我没有做出了，答案很新颖是当天的日期，而且我后面听说才发现，好像每年他都会出现这种当天考试日期的数字（，我当时暴力肯定解不出来，之前看见一个比较好的做法是根据这50个数字的某个倍数去循环，这个方法是比较聪明而且不会超时的，后面我把那篇文章找出来（一时没有找到）

试题 C: 质因数个数 本题总分：10 分 【问题描述】 给定正整数 n，请问有多少个质数是 n 的约数。

 

就是先得到小于n的所有素数，然后看能否被n整除，我其实是担心这个题后面的样例超时的，不知道有没有更优化的方法。

import math
n = int(input())
result=[]
for i in range(2,int(n**(0.5))+1):
    flag = 1
    for j in range(2,int(math.sqrt(i)+1)):
        if i % j == 0:
            flag = 0
            break
    if flag:
        result.append(i)
yueshu=[]
for r in result:
    if n % r == 0:
        yueshu.append(r)
print(len(yueshu))

试题 D: 矩形拼接

 【问题描述】 已知 3 个矩形的大小依次是 a1 × b1, a2 × b2 和 a3 × b3。用这 3 个矩形能拼 出的所有多边形中，边数最少可以是多少？ 例如用 3 × 2 的矩形（用 A 表示）、4 × 1 的矩形（用 B 表示）和 2 × 4 的矩 形（用 C 表示）可以拼出如下 4 边形。

 这道题是完全不太懂，希望有懂的同学可以指导一下！~

 

试题 E: 消除游戏在一个字符串 S 中，如果 S i = S i−1 且 S i , S i+1 ，则称 S i 和 S i+1 为边缘 字符。如果 S i , S i−1 且 S i = S i+1，则 S i−1 和 S i 也称为边缘字符。其它的字符 都不是边缘字符。 对于一个给定的串 S，一次操作可以一次性删除该串中的所有边缘字符 （操作后可能产生新的边缘字符）。 请问经过 2 64 次操作后，字符串 S 变成了怎样的字符串，如果结果为空则 输出 EMPTY。

 

两个题连着不会，光拿分可以试着输出EMPYT应该能骗几分（）

 试题 F: 重新排序【问题描述】 给定一个数组 A 和一些查询 Li , Ri，求数组中第 Li 至第 Ri 个元素之和。 小蓝觉得这个问题很无聊，于是他想重新排列一下数组，使得最终每个查 询结果的和尽可能地大。小蓝想知道相比原数组，所有查询结果的总和最多可 以增加多少?

思路：为了使得最终的结果尽可能的大，就是让重合的区间内的数尽可能地大，先计算原来的和sumPrime，再计算最大值排在重合区间的和sumNew，最后做差就可以得到增加的大小。

n = int(input())
a = list(map(int,input().split())) # n个整数
m = int(input()) # 查询数
cha = []
for i in range(m):
    cha.append(list(map(int,input().split())))
sumPrime = 0
times=[0]*n
for ii in cha:
    l,r = ii
    l=l-1
    r=r-1

    for i in range(l,r+1):
        sumPrime += a[i]
        times[i] += 1
# print(sumPrime)
a.sort() # 对a进行排序
# 对其中的重复区间进行统计
times.sort()
sumNew=0
for i in range(n):
    sumNew += times[i]*a[i]
# print(sumNew)
print(sumNew-sumPrime)

 

试题 G: 全排列的价值【问题描述】 对于一个排列 A = (a1, a2, · · · , an)，定义价值 ci 为 a1 至 ai−1 中小于 ai 的数 的个数，即 bi = |{aj | j < i, aj < ai}|。定义 A 的价值为 ∑n i=1 ci。 给定 n，求 1 至 n 的全排列中所有排列的价值之和。

 

 思路：这道题我是找规律得到的，当时我罗列了一下3、4、5三个数的结果（花了不少时间），发现答案应该是((n-1）*n）/2 *  n! /2，应该是有对称的规律，所以让我想到了累加和和阶乘

比如3就是3×2/2×3！/2=9,4就是4×3/2×4！/2=72，5就是10（1-4的和）×5！/2=600

# 得到排列数*中间的值
n = int(input())
sum = 0
for i in range(n):
    sum+=i
mid = sum
f = 1
for i in range(3,n+1):
    f *= i
a = mid * f
# 3 * 3
# 6 * 12 （4*3）
# 10 * 60
result = a  % 998244353
print(int(result))

试题 H: 最长不下降子序列【问题描述】 给定一个长度为 N 的整数序列：A1, A2, · · · , AN。现在你有一次机会，将其 中连续的 K 个数修改成任意一个相同值。请你计算如何修改可以使修改后的数 列的最长不下降子序列最长，请输出这个最长的长度。 最长不下降子序列是指序列中的一个子序列，子序列中的每个数不小于在 它之前的数。

 思路：是一类叫做最长上升子序列的题，先判断一下是不是全部上升的序列，如果不是全部上升，那一定现在存在一个最长的上升序列，通过一个数组dp存储到这个数字的最长子序列长度，如果该数字比之前最长子序列大，那么dp的值就＋1，否则就不变，然后找到dp数组第一次出现最大值的地方，通过一个判断得到结果。想到这个思路是当时看动态规划的时候，有点类似最小编辑距离，后面再看的时候发现这就是dp中的最长递增子序列的模板题，也很推荐labuladong的算法网站，如果我早看见这个说不定当时就基本不用动脑子了（动态规划设计：最长递增子序列 :: labuladong的算法小抄

n,k = list(map(int,input().split()))
a = list(map(int,input().split()))
# print(n,k)
# print(a)
dp=[1]*n
dp[0]=1
for i in range(1,n):
    for j in range(i):
        temp = 0
        if a[i]>a[j]:
            temp=dp[j]+1
        if temp>dp[i]:
            dp[i]=temp
result=1
l=0
r=0
#print(dp)
if max(dp)==n:
    result=n
else:
    r = n-1-dp.index(max(dp))
    l = dp.index(max(dp))-max(dp)+1
    m = max(l,r)
    if m >= k:
        result = max(dp)+k
    elif m < k:
        result = max(dp)+m
# print(l)
# print(r)
print(result)

试题 I: 最优清零方案【问题描述】 给定一个长度为 N 的数列 A1, A2, · · · , AN。现在小蓝想通过若干次操作将 这个数列中每个数字清零。 每次操作小蓝可以选择以下两种之一： 1. 选择一个大于 0 的整数，将它减去 1； 2. 选择连续 K 个大于 0 的整数，将它们各减去 1。 小蓝最少经过几次操作可以将整个数列清零？

贪婪算法，由于最少多少次，所以优先选取第二个动作，从”连续k个值“的k开始循环到n，找出k个小区间终得最小值m，说明这个区间只能有m次连续区间的减法操作。循环到最后，剩下的值只能通过动作1减去，因此就可以得到答案。

n,k=list(map(int,input().split()))
a  =list(map(int,input().split()))
s=sum(a)
for i in range(k,n+1):

    news=a[i-k:i]
    m   =min(news)
    for j in range(i-k,i):
        a[j] -= m
    s -= m*(k-1)
print(s)

 试题 J: 数的拆分【问题描述】 给定 T 个正整数 ai，分别问每个 ai 能否表示为 x y1 1 · x y2 2 的形式，其中 x1, x2 为正整数，y1, y2 为大于等于 2 的正整数。

 第三个没做出来的题，好像是和数论有关，这个题我后面把我看见那篇比较好的思路加进来。

转眼也写完了，还有很多坑没填，想到什么没写的心得会再补充，请大家不吝赐教！