matlab sym用法_MATLAB的符号运算基础
赞
踩
在数学运算中,运算的结果如果是一个数值,可以称这类运算为数值运算;如果运算结果为表达式,在MATLAB中称为符号运算,符号计算是对未赋值的符号对象(可以是常数、变量、表达式)进行运算和处理。MATLAB具有符号数学工具箱(SymbolicMath Toolbox),将符号运算结合到MATLAB的数值运算环境。符号数学工具箱是建立在Maple软件基础上的。
(一) 符号变量建立符号变量和符号常数
建立符号变量的方法有两种,应用,应用sym与syms函数,通常应用sym建立符号表达式,应用syms同时定义多个符号变量。
(1)函数:sym
功能:用来建立单个符号量
语法形式:sym(‘表达式或变量’)
举例:
- a = sym('a'); %定义符号变量a,下同
- b = sym('b')
- c = sym('c')
- d = sym('d') %至此定义了4个符号变量
- w = 10;x = 5;y = -8;z = 11;
-
- A = [a,b;c,d] %建立符号矩阵A
- B = [w,x;y,z] %建立数值矩阵B
- C = det(A); %计算符号矩阵A的行列式
- D = det(B); %建立数值矩阵B的行列式
可得到如下结果:
由上述结果我们不难看出,在符号运算中是以表达式形式呈现结果的,而在数值运算中是以数值表示结果的。
(2)函数:syms
功能:定义多个符号变量
语法:syms Var1 Var2 ……Varn
说明:函数定义符号变量var1,var2,……,Varn等。在用这种格式定义符号变量时无需在变量名上加字符分解符(‘’),变量间用空格而不要用逗号分隔,要用空格来分隔。
例2:应用syms函数定义符号变量
- syms x y %同时定义x,y为符号变量
- A = [sin(x) sin(y);cos(x) cos(y)]</span>
(二)基本的符号运算
1基本符号运算函数
在MATLAB中,有很多应用于符号运算的函数,常用的函数如下表所示:
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
| 函数名 | 功能 | 用法举例 |
| sym | 字符串或数值到符号的切换 | sym(‘a+b’) |
| expand | 展开 | syms x s = (-7*x^2-8*y^2)*(-x^2+3*y^2); expand(s) collect(s,x) factor(ans) g = simple(ans) |
| collect | 合并同类项 | |
| factor | 因式分解 | |
| simplify simple | 化简 | |
| sym2poly(S) | 转化S为多项式系数向量 | syms x;f=’2*x^2+3*x-5’; n = sym2poly(f) poly2sym(n) |
| poly2sym(c) | 转换多项式系数向量c为符号多项式 |
2符号表达式运算
(1)符号表达式的四则运算
- syms x y z; %定义x,y,z为符号变量
- f1 = 2*x+x^2*x-5*x+x^3
- f2 = 2*x/(5*x)
- f3 = (x+y)*(x-y)</span>
(2)因式分解与多项式展开
函数1:factor
功能:分解因式
语法:factor(s)
说明:s是符号表达式或符号矩阵
函数2:collect
功能:合并同类项
语法:collect(s)
collect(s,x)
说明:对s按符号变量x进行同类项合并,s是符号表达式或符号矩阵。
举例:对表达式
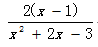
因式分解
- f = sym('2*(x-1)/(x^2+2*x-3)'); %输入表达式
- F = factor(f) %对符号表达式f进行因式分解</span>
(3)表达式化简
MATLAB提供的对符号表达式化简函数为simplify。
函数:simplify
功能:对表达式进行化简
语法:simplfy(S)
- f=cos(x)^2+sin(x)^2
- simplify(f)
注:simplify和simple是Matlab符号数学工具箱提供的两个简化函数,区别如下:
simplify的调用格式为:simplify(S);对表达式S进行化简。
simple是通过对表达式尝试多种不同的方法(包括simplify)进行化简,以寻求符号表达式S的最简形式。
调用方式为:
[r,how]=simple(S);r为返回的简化形式,how为化简过程中使用的一种方法。how有以下几种形式:
(1)simplify 函数对表达式进行化简;
(2)radsimp函数对含根式的表达式进行化简;
(3)combine 函数将表达式中以求和、乘积、幂运算等形式出现的项进行合并;
(4)collet合并同类项
(5)factor函数实现因式分解
(6)convert函数完成表达式形式的转换


